Se você está aqui é porque tem dúvidas sobre como aplicar a ação do vento em estruturas de concreto. Essa é uma dúvida bastante comum quando começamos a estudar sobre ação do vento em estruturas.
Pode ficar tranquilo que explicarei aqui, de maneira didática, como podemos transformar a pressão dinâmica que encontramos até então em uma força em nosso modelo estrutural.
Força de arrasto
A força global do vento é o somatório de todas as ações do vento exercidas sobre uma edificação. Nas edificações de concreto armado buscamos calcular a força de arrasto, que indica a componente da força da direção do vento analisada.
Uma vez que já conhecemos a pressão dinâmica do vento, para obtermos a força de arrasto basta multiplicarmos a pressão dinâmica pela área efetiva de contato e um coeficiente de arrasto, que irá variar de acordo com a forma da edificação.
\mathrm{F_a = C_a \cdot q \cdot A_e}
Coeficiente de arrasto
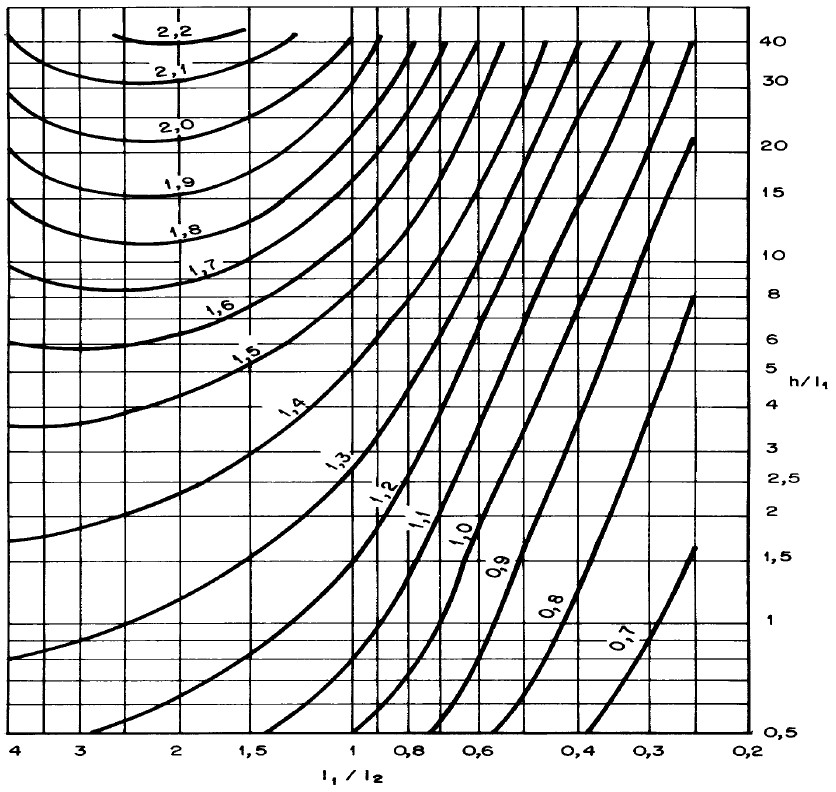
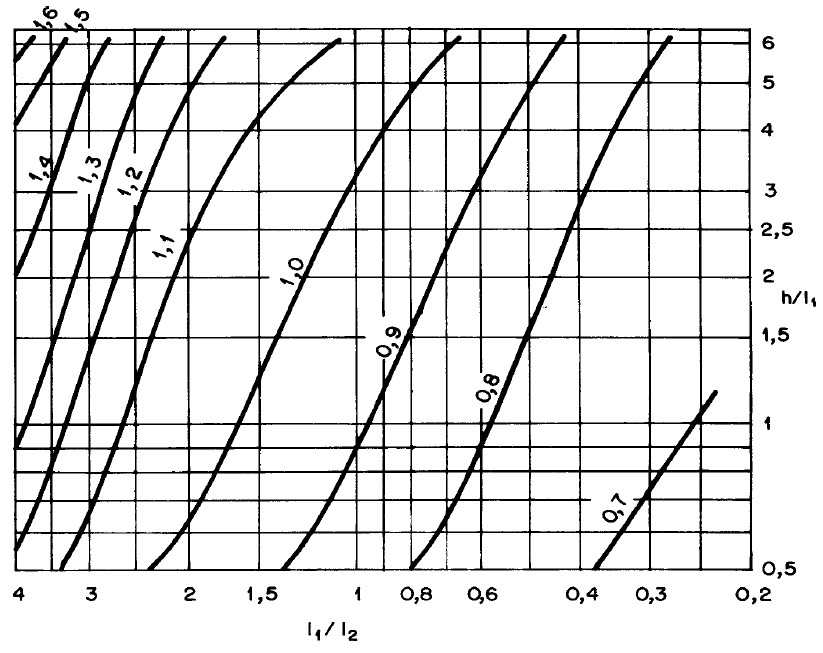
A norma ABNT/NBR: 6123 (1988) apresenta dois ábacos para o cálculo do coeficiente de arrasto. A escolha entre cada um dos ábacos será dada dependendo se a região apresenta ventos de baixa ou alta turbulência.
É importante destacarmos o que a norma considera vento de alta turbulência. Para a norma brasileira, uma edificação em vento de alta turbulência é aquela que não exceder em duas vezes a altura média das edificações vizinhas. Sendo que, as edificações vizinhas estão na direção e sentido do vento, a uma distância de:
- 500 m, para uma edificação de até 40 m de altura;
- 1000 m, para uma edificação de até 55 m de altura;
- 2000 m, para uma edificação de até 70m de altura;
- 3000 m, para uma edificação de até 80 m de altura.
Nós entraremos nos ábacos com as relações \mathrm{\dfrac{h}{l_1}} e \mathrm{\dfrac{l_1}{l_2}}, em que \mathrm{l_1} equivale a largura na dimensão horizontal perpendicular a direção do vento, \mathrm{l_2}, a dimensão horizontal na direção do vento e \mathrm{h}, a altura da edificação, conforme apresenta a figura abaixo.
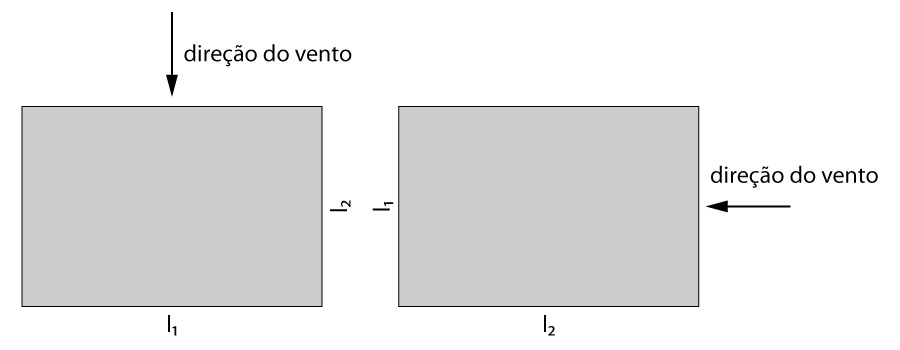
Dessa forma, entraremos nos ábacos para cada direção analisada. Se imaginarmos uma edificação de 20 m x 30 m, para uma direção teremos \mathrm{l_1=20} e \mathrm{l_2=30} e para outra direção teremos \mathrm{l_1=30} e \mathrm{l_2=20}.
Com as relações já calculadas, podemos entrar no ábaco para obtermos os coeficientes de arrasto. Segue abaixo o ábaco para ventos de baixa turbulência:
E agora o ábaco para ventos de alta turbulência:
Distribuindo a ação do vento
Agora que já encontramos a força de arrasto, vamos estudar agora como podemos distribuir a ação do vento dentro dos pórticos da estrutura.
É importante destacar que a norma ainda exige a consideração de uma excentricidade na aplicação da força de arrasto, a fim de considerar o vento agindo obliquamente e os efeitos de vizinhança. Por enquanto seguiremos com o vento agindo perpendicularmente e sem considerar a possibilidade de torção do edifício.
Diafragma rígido
Ao analisarmos a distribuição do vento em estruturas de concreto armado, é importante entendermos o conceito de diafragma rígido.
O diafragma rígido consiste em percebermos que, a ação do vento provoca deformações (encurtamentos e alongamentos) quase nulas nas lajes de concreto armado, de modo que é usual desconsiderarmos. Assim sendo, como não temos deformações no plano da laje, tem-se que os deslocamentos horizontais causados pela estrutura em um mesmo pavimento serão os mesmos para todos os pilares.
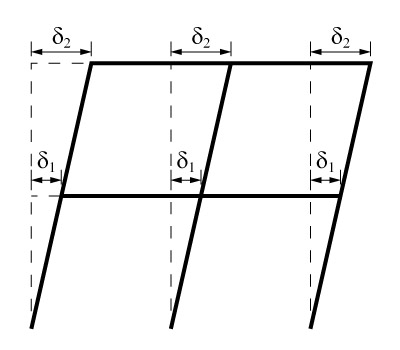
Observe o pórtico na figura acima que a laje de cada pavimento se desloca horizontalmente como um conjunto único.
Inércia equivalente do pórtico
Vamos considerar agora a ação do vento atuando em uma direção em que existem três pórticos, conforme ilustra a figura abaixo.
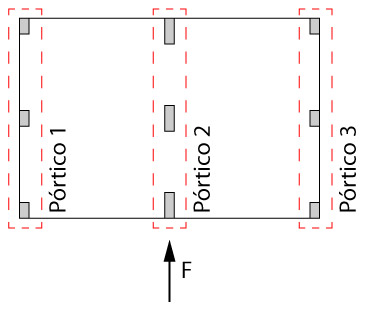
No nível do pavimento analisado, a pressão dinâmica foi transformada em uma força F e aplicada no pavimento. Como essa edificação apresenta lajes de concreto armado, assumiremos o comportamento de diafragma rígido para a mesma, ou seja, uniformizaremos os deslocamentos nos níveis das lajes.
Se tivéssemos três pórticos idênticos, nós teríamos uma força de \mathrm{\dfrac{F}{3}} em cada pórtico, uma vez que os deslocamentos seriam iguais e a rigidez dos três pórticos também.
Na situação apresentada, o pórtico central apresenta uma maior rigidez, fazendo com que o mesmo receba uma parcela maior da força. A parcela da força em cada pórtico é diretamente proporcional a relação de rigidez entre o pórtico analisado e toda a estrutura.
A questão então é…
Como posso mensurar a rigidez de um pórtico?
Uma forma muito utilizada é comparar cada pórtico com um pilar engastado na base e livre no topo.
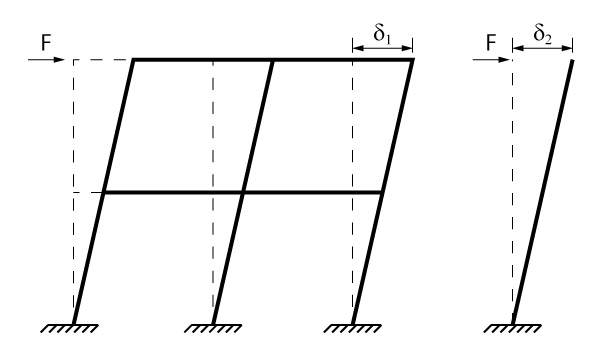
O deslocamento de uma barra engastada e livre pode ser obtido através da equação diferencial da linha elástica. Independente do método utilizado, encontraremos a seguinte formulação:
\mathrm{\delta_2 = \dfrac{F \cdot H^3}{3 \cdot \left( E \cdot I \right)}}
Em que H, equivale a altura total da barra engastada e livre, que será igual a altura do pórtico em questão.
A ideia é considerar que o produto de rigidez \mathrm{E \cdot I} do pórtico é equivalente ao do pilar. Igualando o deslocamento no topo do pórtico e do pilar, teremos:
\mathrm{\left( E \cdot I \right)_{pórtico} = \dfrac{F \cdot H^3}{3 \cdot \delta_1}}
Repartição da Força de Arrasto na prática
No exemplo apresentado acima, temos três pórticos, sendo que dois deles são iguais.
Vamos aplicar no topo de cada um dos pórticos uma força arbitrária (por exemplo, 100 kN) e obter o deslocamento horizontal no último nível. Para isso, podemos utilizar algum software comercial, como por exemplo o Ftool.
Nessa situação, vamos supor que o deslocamento no topo do pórtico central foi de 1 cm e em cada um dos pórticos extremidade foi de 2 cm. Utilizando a formulação apresentada acima, teremos:
\mathrm{\left( E \cdot I \right)_{1} = \dfrac{100 \cdot 6^3}{3 \cdot 0,02} = 3,6 \cdot 10 ^5 \; kN \cdot m^2}
\mathrm{\left( E \cdot I \right)_{2} = \dfrac{100 \cdot 6^3}{3 \cdot 0,01} = 7,2 \cdot 10 ^5 \; kN \cdot m^2}
Então, vamos analisar a rigidez de um pórtico de extremidade em relação a todos os pórticos:
\mathrm{\dfrac{3,6 \cdot 10 ^5}{3,6 \cdot 10 ^5+ 7,2 \cdot 10 ^5+3,6 \cdot 10 ^5} = 0,25}
Verificando agora para o pórtico central:
\mathrm{\dfrac{7,2 \cdot 10 ^5}{3,6 \cdot 10 ^5+ 7,2 \cdot 10 ^5+3,6 \cdot 10 ^5} = 0,50}
Com isso temos que 50% da força F aplicada no pavimento será absorvida pelo pórtico central e 25% da força aplicada será distribuída para os pórticos de extremidade.
Observe que esse resultado era imediato, uma vez que, para a mesma força arbitrária, o pórtico central apresentou metade do deslocamento. Assim sendo, possui o dobro da rigidez e absorve o dobro da força.
Recado final
Você já aprendeu os conceitos necessários sobre a distribuição da força de arrasto para os pórticos da estrutura de contraventamento. Para consolidar bem esse conteúdo, iremos partir agora para a resolução de um exemplo aplicado sobre esse assunto.
Gostaria de ter acesso a um curso sobre modelagem de alvenaria estrutural no Revit?
Aproveite enquanto está com um preço especial.
