Método de Culmann: exercícios resolvidos

Nesse post vamos resolver juntos dois exercícios de análise da estabilidade de taludes pelo método de Culmann!

Aqui mesmo no nosso blog, já tratamos sobre a teoria e desenvolvimento das formulações do método de Culmann.

Indico, inclusive, que você dê uma lida prévia no post anterior para compreender melhor o que faremos aqui.

Mas agora, vamos direto a resolução dos exercícios!

Exercício 1

Considere o seguinte talude apresentado na figura abaixo.

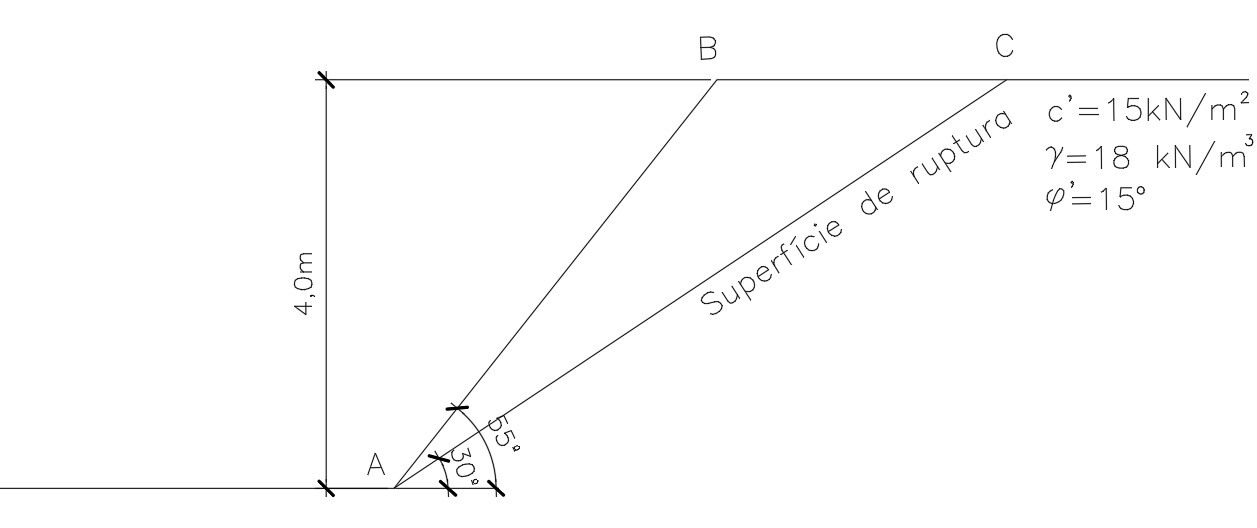
Na figura, AC representa uma possível superfície de rutura. Para a cunha ABC, determine o fator de segurança contra deslizamento a partir do método de Culmann.

Resolução

Então, como você pode perceber trata de um exercício de:

• Talude finito;
• Superfície de ruptura plana.

Portanto, podemos fazer uso do método de Culmann para determinar o fator de segurança contra deslizamento, conforme proposto no exercício.

A seguir, vamos fazer o passo-a-passo para a resolução desse exercício.

Passo 1 – Cálculo do peso da cunha e das suas componentes

Primeiramente, então, vamos calcular o peso da cunha e as componentes normal e tangente à superfície de ruptura.

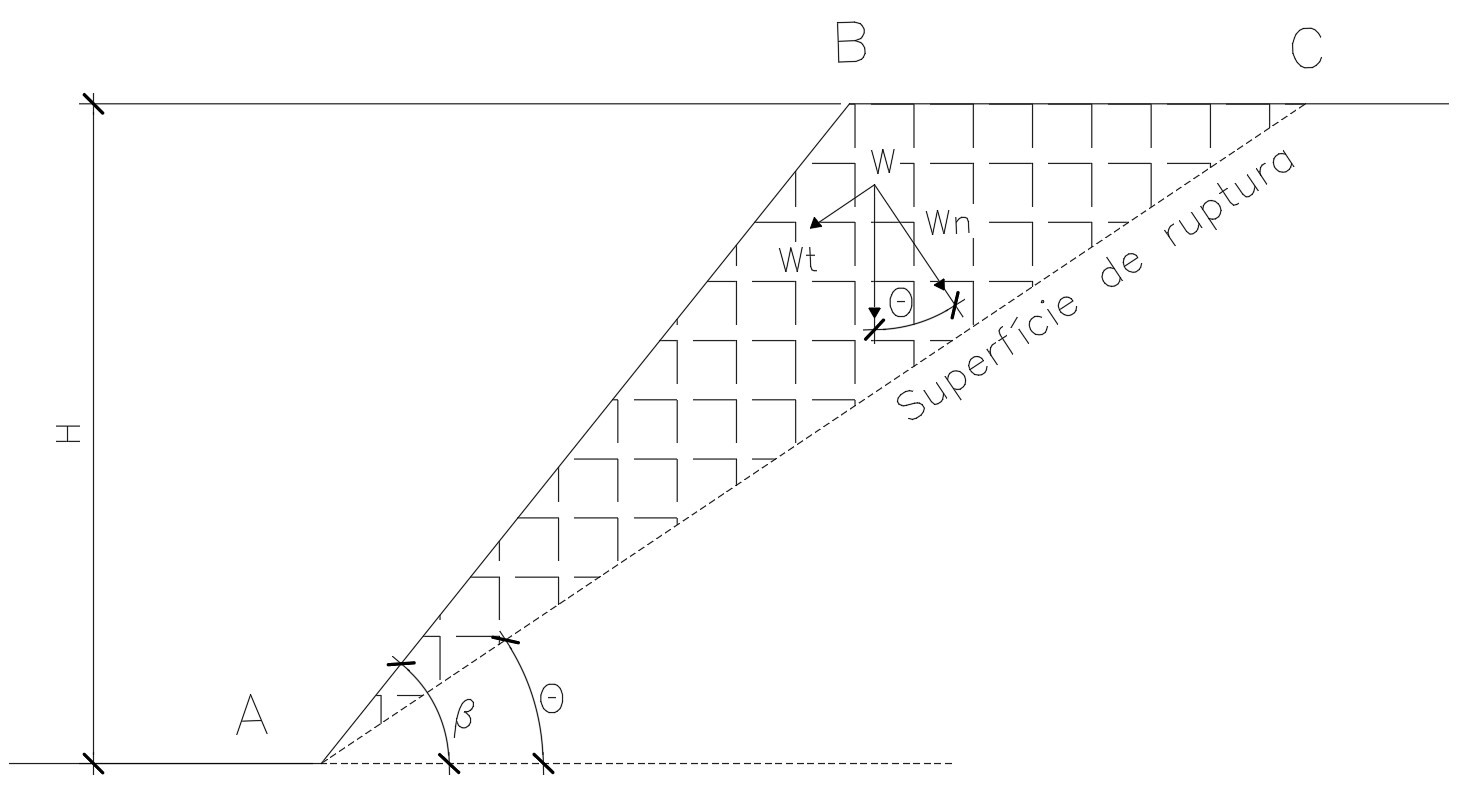
Como vimos no post anterior, podemos calcular o peso da cunha ABC com a seguinte formulação:

\mathrm{W_n=\dfrac{H^2\cdot\gamma[sen(\beta-\theta)]\cdot cos \theta}{2\cdot sen\theta\cdot sen\beta}}

\mathrm{W_t=\dfrac{H^2\cdot\gamma[sen(\beta-\theta)]\cdot sen \theta}{2\cdot sen\theta\cdot sen\beta}}

Então, desenvolvendo essas formulações para os dados da questão, temos:

\mathrm{W_n=\dfrac{H^2\cdot\gamma[sen(\beta-\theta)]\cdot cos \theta}{2\cdot sen\theta\cdot sen\beta}}

\mathrm{W_n=\dfrac{4^2\cdot 18 [sen(55º-30º)]\cdot cos 30º}{2\cdot sen30º\cdot sen55º}}

\mathrm{W_n=128,68 kN}

Analogamente, podemos calcular a componente tangente!

\mathrm{W_t=\dfrac{H^2\cdot\gamma[sen(\beta-\theta)]\cdot sen \theta}{2\cdot sen\theta\cdot sen\beta}}

\mathrm{W_t=\dfrac{4^2\cdot 18 [sen(55º-30º)]\cdot sen 30º}{2\cdot sen30º\cdot sen55º}}

\mathrm{W_t=74,29 kN}

Agora que já calculamos as componentes do peso da cunha, vamos calcular a resistência média de cisalhamento.

Passo 2 – Cálculo da resistência média de cisalhamento

O cálculo da resistência média de cisalhamento é feito com a seguinte formulação:

\mathrm{\tau_r=c^{'}+\sigma^{'}\cdot tan\phi^{'}}

Onde:

• \mathrm{c^{'}}: coesão efetiva do solo;
• \mathrm{\sigma^{'}}: tensão normal efetiva;
• \mathrm{\phi^{'}}: ângulo de atrito efetivo do solo;

Já vimos no post anterior também que:

\mathrm{\sigma^{'}=\dfrac{H\cdot\gamma[sen(\beta-\theta)]\cdot cos \theta}{2\cdot sen\beta}}

Então:

\mathrm{\sigma^{'}=\dfrac{4\cdot 18[sen(55º-30º)]\cdot cos30º}{2\cdot sen55º}}

\mathrm{\sigma^{'}=16,08 kN/m²}

Portanto, temos que:

\mathrm{\tau_r=15+16,08\cdot tan15º}

\mathrm{\tau_r=19,31 kN/m²}

Passo 3 – Cálculo da tensão de cisalhamento atuante

Agora, precisamos calcular a tensão de cisalhamento atuante para conseguirmos determinar o fator de segurança.

Da mesma forma que fizemos para a resistência média de cisalhamento, já tratamos disso no post anterior, onde chegamos à seguinte formulação:

\mathrm{\tau_a=\dfrac{H\cdot\gamma[sen(\beta-\theta)]sen\theta}{2\cdot sen\beta}}

\mathrm{\tau_a=\dfrac{4\cdot18[sen(55º-30º)]sen30º}{2\cdot sen55º}}

\mathrm{\tau_a=9,29 kN/m²}

Então, agora basta apenas calcularmos o fator de segurança contra o deslizamento do talude.

Passo 4 – Determinação do fator de segurança

Como já vimos em posts anteriores, podemos calcular o fator de segurança contra do deslizamento da seguinte forma:

\mathrm{FS=\dfrac{\tau_r}{\tau_a}}

Onde:

• \mathrm{\tau_r}: tensão de cisalhamento média resistentes do solo;
• \mathrm{\tau_a}: tensão de cisalhamento atuante na superfície de ruptura analisada.

Portanto, basta que façamos a divisão dos valores de tensão já calculados anteriormente.

Então, temos:

\mathrm{FS=\dfrac{19,31}{9,29}}

\mathrm{FS=2,08}

Como FS>1,5, podemos afirmar que para a superfície de ruptura analisada, podemos atestar a segurança à deslizamento do talude!

Exercício 2

Deve ser realizado um corte em um solo, com as seguintes características:

• \mathrm{\gamma=19 kN/m^3};
• \mathrm{c'=12 kN/m^2};
• \mathrm{\phi'=20º}.

A face do corte formará um ângulo de 50º com a horizontal, conforme ilustrado na figura abaixo.

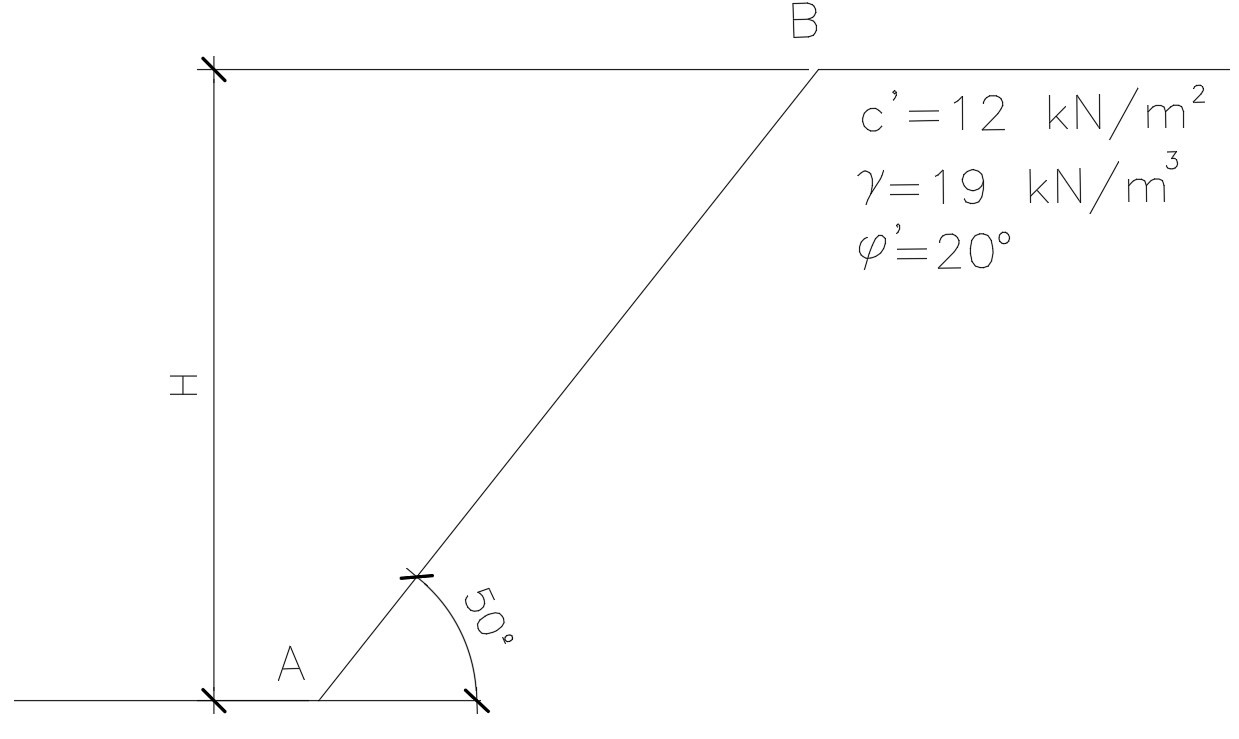
Determine qual é a altura máxima que H pode assumir para que se tenha um fator de segurança FS=2,0.

Resolução

Então, essa questão trata-se de um exercício de cálculo da altura crítica de um talude, segundo o método de Culmann.

Primeiramente, como o exercício não nos dá uma superfície de ruptura para analisarmos o fator de segurança de uma cunha em específico, precisamos considerar uma superfície crítica.

O plano de ruptura crítico para um talude será aquele com uma inclinação \mathrm{\theta} em que a coesão desenvolvida será máxima.

Porém, esse conceito é válido para um FS=1,0. Como o exercício determina que o FS=2,0, temos que:

\mathrm{FS_c=\dfrac{c'}{c_d}}

\mathrm{FS_\phi=\dfrac{tan\phi'}{tan\phi_d}}

Então, desenvolvendo essas formulações, teremos o seguinte valor para a coesão desenvolvida:

\mathrm{FS_c=\dfrac{c'}{c_d}}

\mathrm{2.0=\dfrac{12}{c_d}}

\mathrm{c_d=6 kN/m^2}

Analogamente, temos que o ângulo de atrito interno desenvolvido será:

\mathrm{FS_\phi=\dfrac{tan\phi'}{tan\phi_d}}

\mathrm{2,0=\dfrac{tan20º}{tan\phi_d}}

\mathrm{\phi_d=10,31º}

Agora que já calculamos a coesão desenvolvida e o ângulo de atrito interno desenvolvido, podemos fazer uso da formulação apresentada no post anterior:

\mathrm{H_{cr}=\dfrac{4c'}{\gamma}\cdot\dfrac{sen\beta\cdot cos\phi'}{1-cos(\beta-\phi')}}

\mathrm{H_{cr}=\dfrac{4\cdot 6}{19}\cdot\dfrac{sen50º\cdot cos10,31º}{1-cos(50º-10,31º)}}

\mathrm{H_{cr}=4,13m}

Ou seja, a altura máxima que o talude pode ter para o corte de 50º com a horizontal é de 4,13m.

 

Então, por hoje é isso, pessoal!

Espero que você tenha gostado da leitura e tenha aprendido tudo sobre a aplicação do método de Culmann para a análise de estabilidade de taludes finitos!

Porém, se ficou com alguma dúvida, não se acanhe! Deixe seu comentário aqui embaixo que a gente responde!

Continue seguindo nosso blog e nos acompanhando no YouTube.

Dessa forma, fico por aqui! Até  a próxima =)