Nesse post você vai ver tudo sobre a análise de estabilidade de taludes finitos através do Método de Culmann!
Caso você tenha caído de pára-quedas nesse post, recomendo fortemente que você leia os seguintes posts:
- Tipos de escorregamentos de terra;
- Análise de estabilidade de taludes;
- Soluções de estabilização de taludes;
- Estabilidade de taludes infinitos.
Te prometo que ao final desse post, você saberá analisar um talude finito com ruptura linear pelo método de Culmann.
Agora, sem mais delongas, vamos direto ao conteúdo!
Análise de estabilidade de taludes
Inicialmente, vamos falar sobre a análise de estabilidade de taludes.
Eu sei que já falamos muito sobre isso em outros posts, mas nunca é demais relembrar =)
Então, para analisarmos um talude, basicamente vamos calcular o fator de segurança para uma determinada possível superfície de ruptura.
Como o método de Culmann é utilizado para a análise de taludes finitos com superfície de ruptura linear, considere o seguinte esquema.
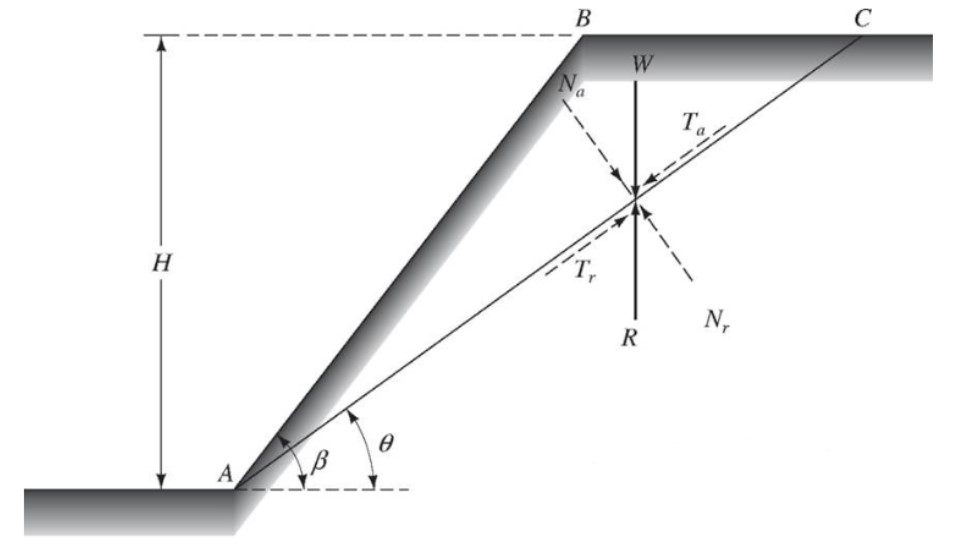
Você pode perceber então, que para uma superfície de ruptura linear, vamos comparar os módulos das forças de cisalhamento resistentes (Tr) e atuantes (Ta), de tal forma que o fator de segurança será:
\mathrm{FS=\dfrac{\tau_r}{\tau_a}}
Onde:
- \mathrm{\tau_r}: tensão de cisalhamento média resistentes do solo;
- \mathrm{\tau_a}: tensão de cisalhamento atuante na superfície de ruptura analisada.
Lembrando que:
- FS<1,0: podemos afirmar que o talude está instável.
- FS=1,0: o talude está em equilíbrio limite, na iminência de movimentação;
- FS>1,0: podemos afirmar que para valores superiores a 1,0, o talude é estável.
Na prática são indicados valores de FS>1,5 para elaboração de projetos de taludes estáveis.
Então, agora que já demos uma breve revisão sobre análise de estabilidade de taludes, vamos estudar o método de Culmann propriamente dito!
Método de Culmann
Como já falamos anteriormente, é preciso entender que o método de Culmann é utilizado para uma situação em específico:
- Taludes finitos;
- Superfície de ruptura linear.
Logo, é importante que você entenda que em outras situações o método de Culmann não é indicado!
Agora, vamos fazer a análise do talude analogamente ao como fizemos para taludes infinitos.
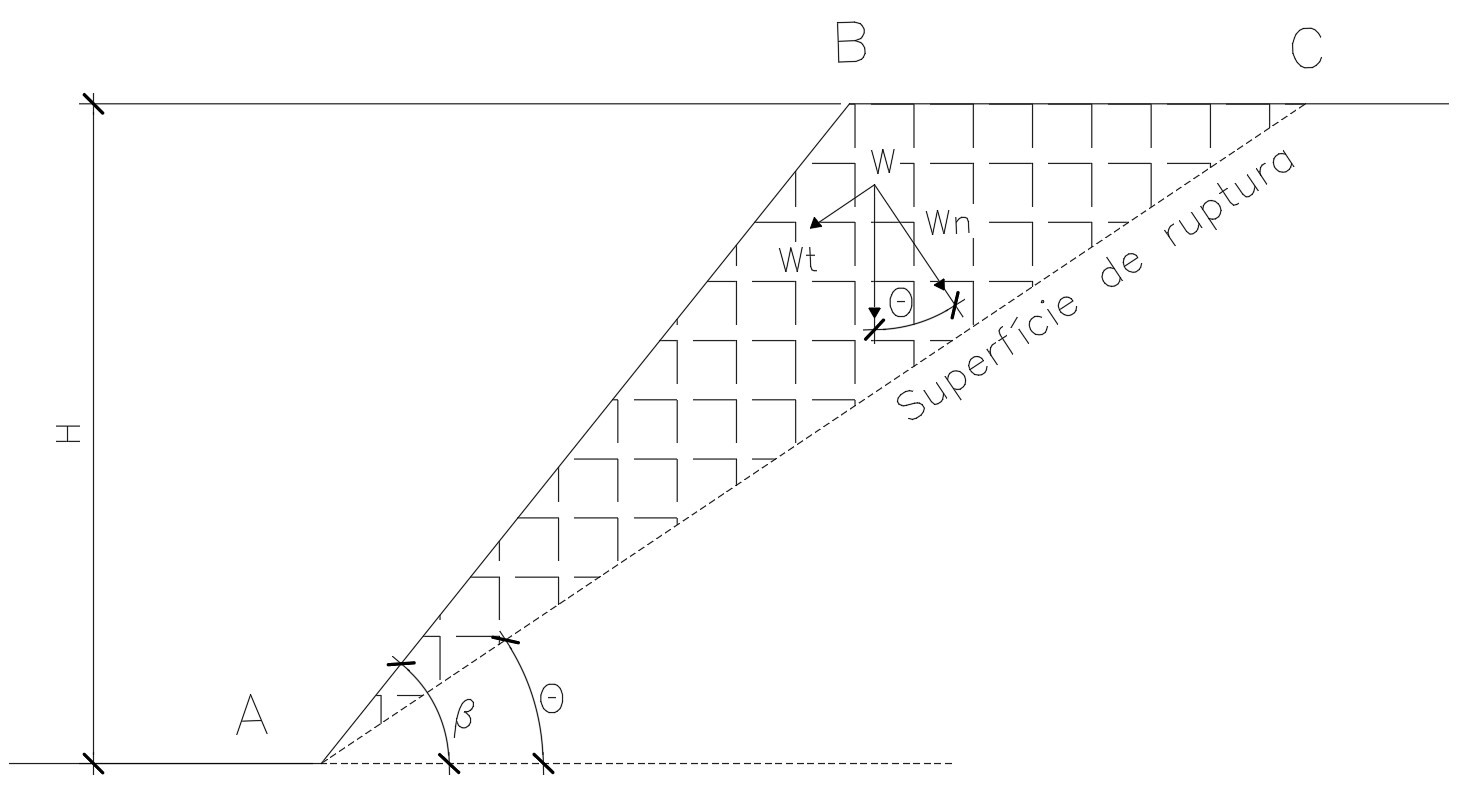
Como você pode perceber pela figura acima, podemos decompor o peso do talude (W) em uma parcela normal à superfície de ruptura (Wn) e uma parcela tangente à essa superfície (Wt). De forma que:
\mathrm{Wn=W\cdot cos\theta}
\mathrm{Wt=W\cdot sen\theta}
Onde:
- W: peso da cunha do talude (hachurado na figura acima)
Cálculo do peso da cunha do talude (W)
Então, agora que já sabemos a decomposição de forças, precisamos determinar o valor do peso da cunha do talude que pode sofrer deslizamento, aqui representado por W.
Perceba, pela figura acima, que tal cunha é um triângulo. Dessa forma, podemos calcular a área da seção transversal hachurada da seguinte forma:
\mathrm{Area=(BC)\cdot H/2}
Podemos dizer, então, que para 1,0m de largura desse talude, temos que:
\mathrm{W=\dfrac{(BC)\cdot H\cdot\gamma}{2}}
Onde:
- \mathrm{\gamma}: peso específico do solo.
Enfim, perceba que agora basta que determinemos os valores de BC e AC para chegarmos à formulação final.
Então, para isso, vamos considerar a seguinte figura que preparei para facilitar sua compreensão.
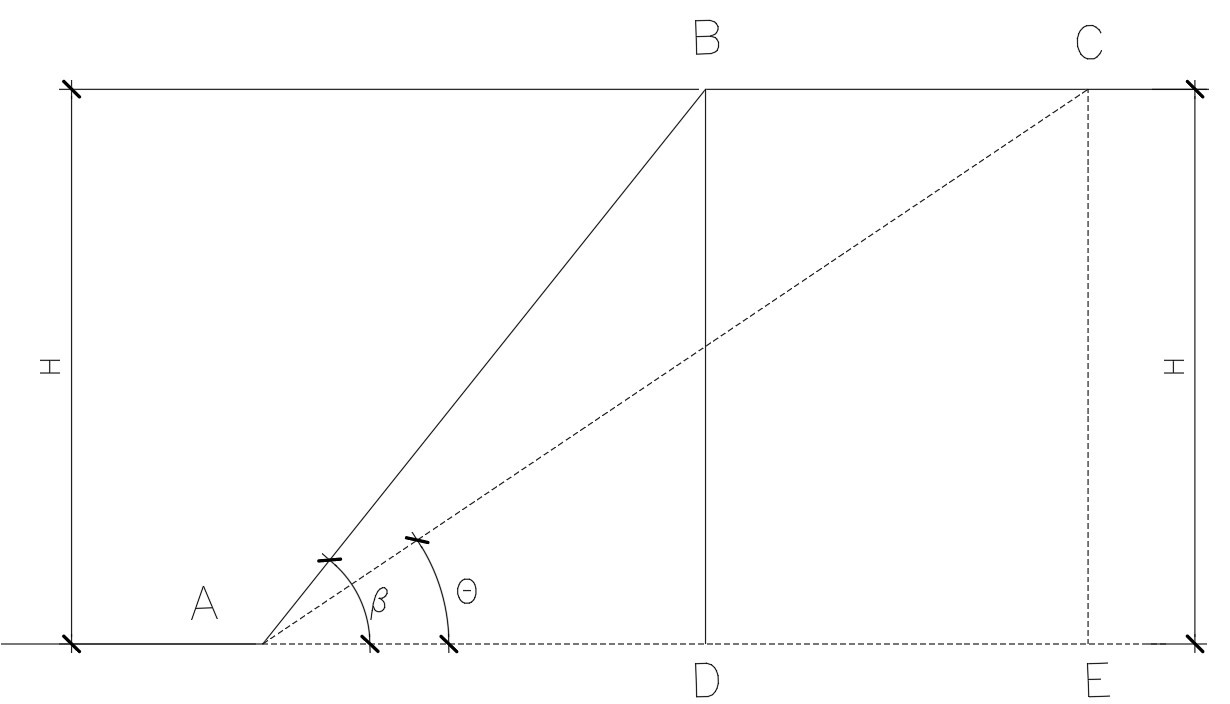
Analisando os triângulos ABD e ACE, perceba que:
\mathrm{DE=BC} e \mathrm{BC=AE-AD}
Logo:
\mathrm{BC=H\cdot cotg\theta - H\cdot cotg \beta}
\mathrm{BC=H(cotg\theta - cotg\beta)}
Desenvolvendo, temos:
\mathrm{BC=H(\dfrac{cos\theta}{sen\theta} - \dfrac{cos\beta}{sen\beta})}
\mathrm{BC=H(\dfrac{cos\theta\cdot sen\beta-cos\beta\cdot sen\theta}{sen\theta\cdot sen\beta})}
Então, lembrando dos conceitos de trigonometria:
\mathrm{BC=H[\dfrac{sen(\beta-\theta)}{sen\theta\cdot sen\beta}]}
Podemos então, determinar as parcelas normal e tangente do peso da cunha:
\mathrm{W_n=\dfrac{H^2\cdot\gamma[sen(\beta-\theta)]\cdot cos \theta}{2\cdot sen\theta\cdot sen\beta}}
\mathrm{W_t=\dfrac{H^2\cdot\gamma[sen(\beta-\theta)]\cdot sen \theta}{2\cdot sen\theta\cdot sen\beta}}
Pronto, agora já sabemos qual o peso da cunha e sua decomposição nas direções normal e tangente à superfície de ruptura.
Agora, vamos calcular as tensões de cisalhamento média resistente e de cisalhamento atuante na superfície de ruptura.
Cálculo da resistência média de cisalhamento (\mathrm{\tau_r})
Para o cálculo da resistência média de cisalhamento, vamos utilizar o critério de Mohr-Coulomb, ou seja:
\mathrm{\tau_r=c^{'}+\sigma^{'}\cdot tan\phi^{'}}
Onde:
- \mathrm{c^{'}}: coesão efetiva do solo;
- \mathrm{\sigma^{'}}: tensão normal efetiva;
- \mathrm{\phi^{'}}: ângulo de atrito efetivo do solo;
Mas isso eu tenho certeza que você já sabia, pois sei que você acompanha nosso conteúdo, não é mesmo? =)
Também sabemos que:
\mathrm{\sigma^{'}=\dfrac{W_n}{AC}}
Logo:
\mathrm{\sigma^{'}=\dfrac{H\cdot\gamma[sen(\beta-\theta)]\cdot cos \theta}{2\cdot sen\beta}}
Agora, então, vamos determinar a tensão média atuante na superfície de ruptura!
Cálculo da tensão de cisalhamento atuante (\mathrm{\tau_a})
Vamos considerar a mesma figura já apresentada anteriormente.

Então, pela definição de tensão e, considerando a largura de 1,0m para o talude, temos que:
\mathrm{\tau_a=\dfrac{Wt}{AC}}
Porém, já havíamos determinado o valor de Wt, então temos que:
\mathrm{\tau_a=\dfrac{H\cdot\gamma[sen(\beta-\theta)]sen\theta}{2\cdot sen\beta}}
Agora que já determinamos a resistência média de cisalhamento e a tensão de cisalhamento atuante, podemos calcular o fator de segurança.
Cálculo do fator de segurança
Por fim, para finalizarmos toda a teoria do nosso conteúdo sobre método de Culmann, vamos determinar o fator de segurança do talude.
Como já falamos anteriormente:
\mathrm{FS=\dfrac{\tau_r}{\tau_a}}
Logo, basta fazermos a relação entre as duas grandezas já calculadas anteriormente!
Altura crítica de acordo com o método de Culmann
Então, nós já mostramos o passo-a-passo para a determinação do fator de segurança em um talude finito.
Porém, vamos agora pensar por uma outra perspectiva, que também é muito usual em obras de engenharia.
Imagine o seguinte talude apresentado abaixo.
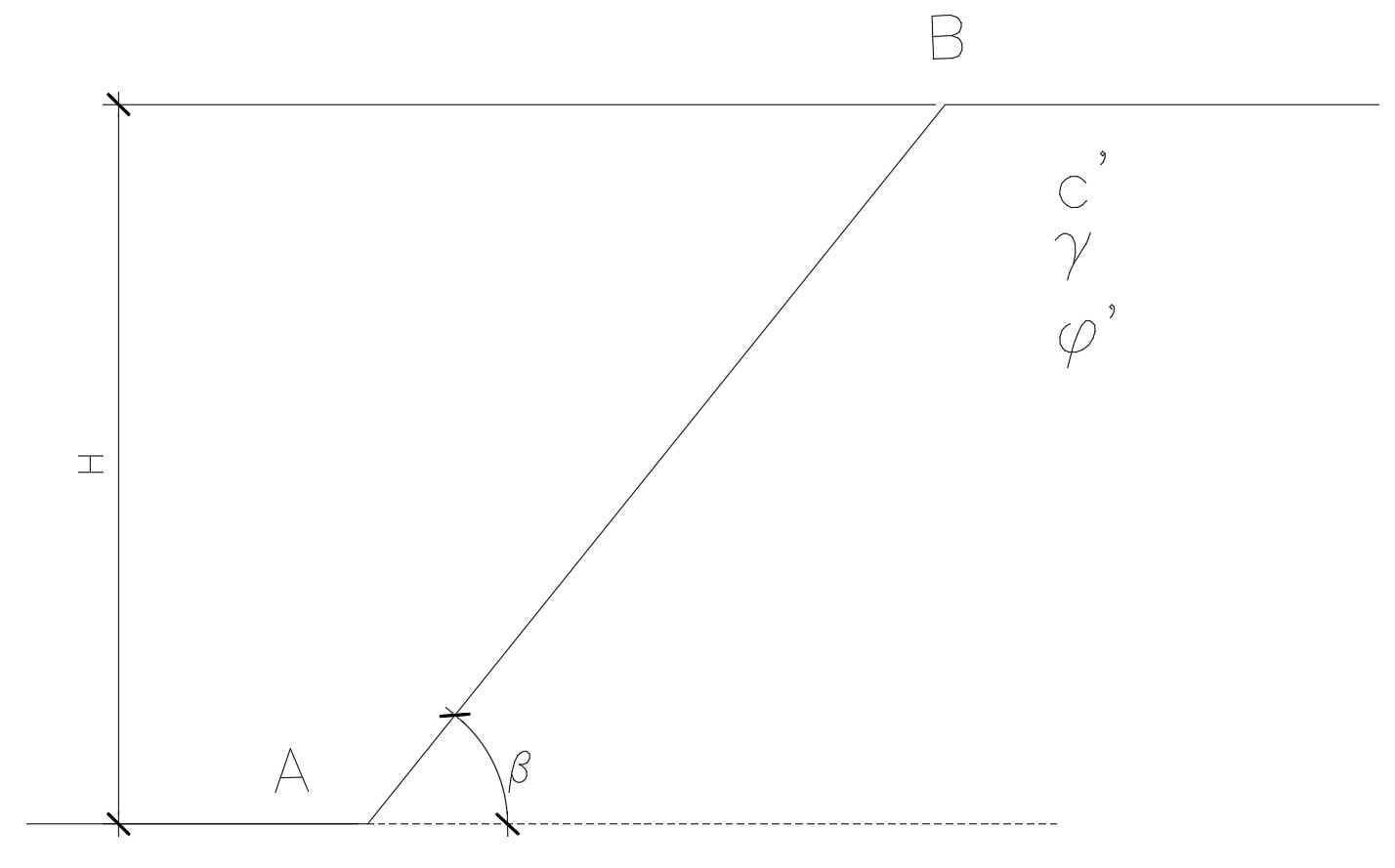
E se eu perguntasse: qual a máxima altura que esse talude pode ter para que se possa garantir sua segurança?
Perceba que é um questionamento diferente do apresentado anteriormente, porém podemos utilizar os conhecimentos já estudados acerca de análise de estabilidade de taludes e método de Culmann.
O plano de ruptura crítico para um talude será aquele com uma inclinação \mathrm{\theta} em que a coesão desenvolvida será máxima.
Desenvolvendo os equacionamentos e considerando a coesão desenvolvida (cd) igual a coesão efetiva c’, podemos chegar à seguinte formulação para a altura crítica.
\mathrm{H_{cr}=\dfrac{4c'}{\gamma}\cdot\dfrac{sen\beta\cdot cos\phi'}{1-cos(\beta-\phi')}}
Onde:
- \mathrm{c'}: coesão efetiva do solo;
- \mathrm{]phi'}: ângulo de atrito interno do solo.
Vale lembrar também que tal altura crítica é dada para um FS=1,0, visto que consideramos cd=c’.
Caso você queira determinar a altura crítica para um outro fator de segurança, basta relembrar do que já vimos em posts anteriores:
\mathrm{FS_c=\dfrac{c'}{c_d}}
\mathrm{FS_\phi=\dfrac{tan\phi'}{tan\phi_d}}
Uffa, hoje tivemos muito conteúdo, mas acabamos por aqui!
Espero que você tenha gostado e tenha entendido tudo.
Porém, caso tenha ficado alguma dúvida, pode deixar nos comentários que vai ser um prazer responder você!
E também não deixa de conferir nosso post com exercícios resolvidos de método de Culmann!
Então, continue seguindo nosso blog e de nos acompanhar também no YouTube.
Até o próximo post =)
Engenheiro Civil, Especialista em Estruturas e Fundações. Ex-goleiro, Pseudosommelier de Cervejas e Poeta Freelancer Fajuto.

obrigado, me salvou!! 🙂
boa tarde como achar o angulo θ? é uma estimativa?