Laje em balanço: 3 passos para o dimensionamento

Nessa publicação você irá aprender como dimensionar uma laje em balanço, ou seja, com o apoio garantido apenas pelo engastamento em uma viga submetida à torção ou uma laje interna. Vamos realizar esse dimensionamento em apenas três passos:

1. Obtenção dos esforços
2. Cálculo da armação de flexão
3. Detalhamento da armação

Antes de partirmos para o dimensionamento de uma marquise em balanço, gostaria de destacar uma pergunta que recebo bastante:

Qual o tamanho máximo de uma laje em balanço?

É importante entendermos que nunca teremos respostas diretas assim dentro do cálculo estrutural. Durante o cálculo de uma laje em balanço existem inúmeras variáveis, por exemplo: vão, carregamento atuante, qualidade da execução, qualidade do concreto, condições de apoio da laje etc. Além disso, lembre-se que um grande limitante de estruturas em balanço são os grandes carregamentos apresentados.

Esforços em uma laje em balanço

Modelo numérico

Uma vez que uma laje em balanço trabalha unicamente na direção do balanço, as mesmas podem ser calculadas como vigas retangulares, engastadas em uma extremidade e livre na outra, com uma faixa arbitrária. A fim de facilitar os cálculos, recomendo utilizarmos uma faixa de 1,0 m de largura.

O vão efetivo para lajes é obtido após adicionar os valores \mathrm{a_1} e \mathrm{a_2} ao vão interno da mesma.

\mathrm{l_{ef} = l_0 + a_1 + a_2}

Os valores \mathrm{a_1} e \mathrm{a_2} assumirão o menor valor entre a metade da largura da viga e 30% da espessura da laje. As variáveis envolvidas são apresentadas na figura abaixo:

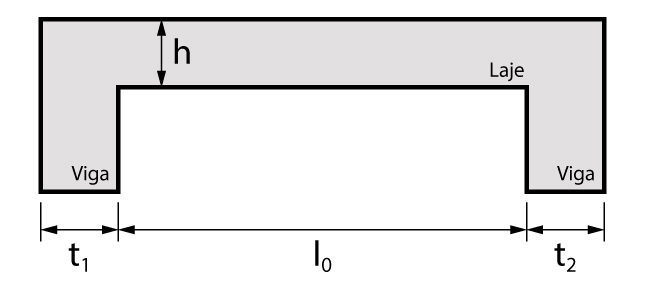
\mathrm { a_1 \leq \left\{ \begin{array}{ll} 0,5 \cdot t_1 \\ 0,3 \cdot h \end{array} \right. }

\mathrm { a_2 \leq \left\{ \begin{array}{ll} 0,5 \cdot t_2 \\ 0,3 \cdot h \end{array} \right. }

Coeficiente adicional para laje em balanço

No dimensionamento de marquise, similar ao já comentado em pilares, a norma ABNT/NBR: 6118 (2014) fornece um coeficiente adicional \mathrm{\gamma_n} para laje em balanço com espessura inferior a 19 cm. Esse coeficiente pode ser calculado através da equação abaixo.

\mathrm{\gamma_n = 1,95-0,05 \cdot h}

A fim de agilizar a obtenção desse valor, a norma também fornece a tabela abaixo, que é aplicação direta da equação.

Antes que avancemos para o próximo passo, vale lembrar que no caso do engastamento da laje em balanço ser dado por uma viga, essa viga deve ser dimensionada e detalhada à torção.

Dimensionamento de marquise

Uma vez que já obtivemos os esforços distribuídos a cada metro para a laje em balanço, o passo seguinte é o dimensionamento da laje em si. Conforme já comentado anteriormente, a mesma deve ser dimensionada como uma seção retangular.

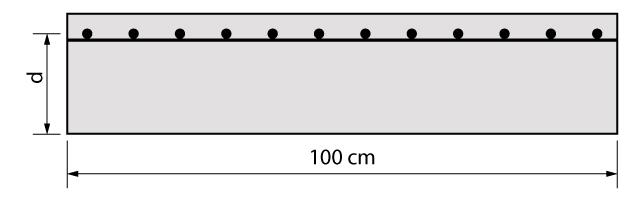
Conforme apresenta a figura acima, o dimensionamento será realizado considerando uma seção com 100 cm de largura e portando, retornando uma área de aço a cada 100 cm também.

Detalhamento de laje em balanço

A área de aço dimensionada pelo procedimento acima será posicionada na face superior da peça, na direção do balanço. Assim sendo, teremos um maior braço de alavanca para a armadura principal.

Na outra direção do negativo utiliza-se uma armadura de distribuição.

Para a armação positiva é possível dispor apenas uma armadura mínima para as duas direções.

Para a execução de uma laje em balanço, devemos ter um cuidado extra sobretudo no posicionamento da armação principal, nos atentando para que essa não desça durante a concretagem, com efeito de redução do braço de alavanca.

Retirada das escoras em laje em balanço

Além disso, durante a execução da obra devemos chamar atenção para o sentido de retirada do escoramento.

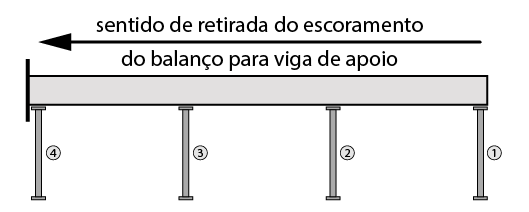
As escoras devem ser retiradas do balanço para dentro, uma vez que, caso seja feito do apoio para o balanço, antes da retirada a última escora teremos uma situação biapoiada.

Exercício de dimensionamento de laje em balanço

Com o intuito de estudarmos o cálculo de marquises iremos utilizar uma laje em balanço de 2,6 m de largura, 1,5 m de balanço e 10 cm de espessura. Além disso, para essa estrutura utilizaremos um concreto classe C20 (resistência característica de 20 MPa) e aço CA50 (tensão de escoamento de 500 MPa).

A laje em questão está ilustrada na figura abaixo:

Com a finalidade de melhorar o entendimento, preparei também um modelo 3d da marquise em questão:

Caso você prefira aprender através de videoaulas, você pode acompanhar a resolução da questão pelo nosso YouTube:

Cálculo do vão efetivo

Antes que possamos avançar no modelo estrutural e nos carregamentos precisamos calcular vão efetivo dessa laje. Conforme você aprendeu anteriormente, devemos analisar o menor entre os seguintes valores: 50% da largura do apoio da laje e 30% da altura da laje.

\mathrm { a_1 \leq \left\{ \begin{array}{ll} 0,5 \cdot t_1 \\ 0,3 \cdot h \end{array} \right. }

\mathrm { a_1 \leq \left\{ \begin{array}{ll} 0,5 \cdot 20 \\ 0,3 \cdot 10 \end{array} \right. }

\mathrm{a_1 = 3 \; cm}

Podemos agora calcular o vão efetivo:

\mathrm{l_{ef} = l_0 + a_1}

\mathrm{l_{ef} = 150 + 3 = 153 \; cm}

Carregamentos

Os três carregamentos que, nesse exemplo, estão atuando na marquise são: peso próprio da laje, carregamento acidental (sobrecarga de utilização) e revestimento.

Analisando primeiramente o peso próprio, basta multiplicar a espessura da laje pelo peso específico do concreto armado (25 kN/m³):

\mathrm{g_1 = 0,1 \; m \cdot 25 \; kN/m^3 = 2,5 \; kN/m^2}

Em segundo lugar, o revestimento será considerado 1 kN/m²:

\mathrm{g_2 = 1,0 \; kN/m^2}

Por fim, o carregamento acidental será utilizado o valor para forros, sem acesso as pessoas, de acordo com ABNT/NBR: 6120 (1980), de 0,5 kN/m²:

\mathrm{q = 0,5 \; kN/m^2}

Portanto, o carregamento total atuante na laje em balanço será:

\mathrm{p = 2,5+1,0+0,5 = 4,0 \; kN/m^2}

Cálculo dos esforços

O carregamento distribuído de valor 4,0 kN/m² pode ser distribuído linearmente ao analisarmos uma faixa de 1,0 m de laje. A figura abaixo apresenta o modelo de cálculo para uma faixa de 1,0 m da marquise em questão.

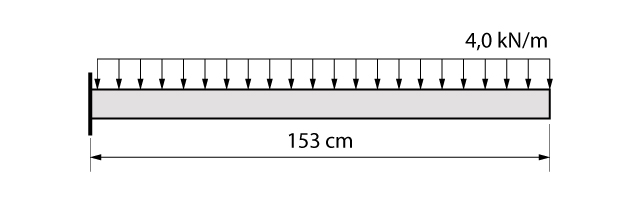
Assim sendo, o momento fletor máximo pode ser calculado por:

\mathrm{M_{máx} = q \cdot L \cdot \dfrac{L}{2} =4 \cdot 1,53\cdot \dfrac{1,53}{2}}

\mathrm{M_{máx} = 4,68 \; kN \cdot m = 468 \; kN \cdot cm}

Cálculo de armadura principal

Em seguida, iremos para o cálculo da altura útil. Uma vez que a laje possui 10 cm de altura, cobrimento igual a 2 cm e admitindo inicialmente uma armação de 10 mm de diâmetro teremos:

\mathrm{d = h - c - \dfrac{\phi}{2} = 10 - 2 - \dfrac{1}{2} = 7,5 \; cm}

Com o propósito de acelerarmos a resolução, o dimensionamento da armadura principal será realizado de acordo com a tabela de KMD presente em Carvalho e Figueiredo Filho (2014).

\mathrm{KMD = \dfrac{M_d}{b_w \cdot d^2 \cdot f_{cd}}}

\mathrm{KMD = \dfrac{1,4 \cdot 1,45 \cdot 468}{100 \cdot 7,5^2 \cdot \dfrac{2,0}{1,4}} = 0,12}

Buscando o KMD de 0,13 na tabela encontra-se um KZ de 0,9236 e uma deformação no aço de 10‰, o que deixa claro que a armação está escoando e podemos utilizar sua tensão de escoamento.

\mathrm{As = \dfrac{M_{Sd}}{KZ \cdot d \cdot f_s}}

\mathrm{As = \dfrac{1,4 \cdot 1,45 \cdot 468}{0,9236 \cdot 7,5 \cdot \dfrac{50}{1,15}} = 3,15 \; cm^2}

Caso prefira não utilizar a tabela, o cálculo da área de aço é realizada da mesma forma do realizado no dimensionamento de vigas de concreto, bastando lembrar que estaríamos dimensionando uma viga de 100 cm de largura.

Da mesma forma, podemos conferir o resultado utilizando nossa Calculadora de Vigas aqui do blog:

[formulario-calculadora-flexao]

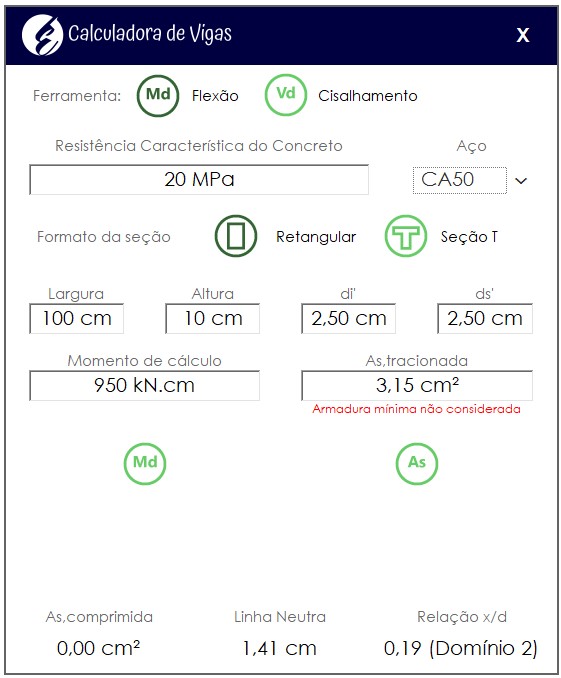
Armadura mínima para laje em balanço

Considerando que para concretos C20 o valor de \mathrm{\rho_{mín}} vale 0,15% (taxa de armação mínima) e que para armação negativa com continuidade devemos utilizar esse valor:

\mathrm{A_{s,mín}=\rho_{mín} \cdot b_w \cdot h}

\mathrm{A_{s,mín}=\dfrac{0,15}{100} \cdot 100 \cdot 10}

\mathrm{A_{s,mín}= 1,5 cm^2/m}

Como o valor calculado foi superior a armadura mínima, utilizaremos o valor de calculado de 3,15 cm²/m.

Lembre-se que o momento que utilizamos para realizar o dimensionamento foi decorrente de um trecho de 1,0 m de largura. Dessa forma, deveremos utilizar 3,15 cm² a cada metro de marquise.

Cálculo da outra direção negativa

Araújo (2014) recomenda a utilização de uma armadura de distribuição para a outra direção da armação negativa.

O norma brasileira fornece taxas mínimas para armações de distribuição (secundárias) apenas positivas. Utilizaremos as mesmas nesse exercício:

• \mathrm{As/s \geq} 20% da armadura principal
• \mathrm{A_s/s \geq 0,9 \; cm^2/m}
• \mathrm{\rho_s \geq 0,5 \cdot \rho_{mín}}

Como a norma também fornece um valor de 0,67 da taxa mínima para armadura negativa de bordas sem continuidade ao invés dos 0,5 descritos acima. Com isso, ficaremos com:

• \mathrm{As/s \geq} 20% da armadura principal = \mathrm{0,2 \cdot 3,15 = 0,63 \; cm^2/m}
• \mathrm{A_s/s \geq 0,9 \; cm^2/m}
• \mathrm{\rho_s \geq 0,67 \cdot \dfrac{0,15}{100} = \dfrac{0,10}{100}}

\mathrm{A_{s,dist}=\dfrac{0,10}{100} \cdot 100 \cdot 10}

\mathrm{A_{s,dist}= 1,0 cm^2/m}

Cálculo das armaduras positivas

Para a armação positiva utilizaremos 0,67 da taxa de 0,15%, ou seja, 0,10% da área de concreto:

\mathrm{A_{s,pos}=\dfrac{0,10}{100} \cdot 100 \cdot 10}

\mathrm{A_{s,pos}= 1,0 cm^2/m}

Detalhamento da laje em balanço

Segue abaixo um resumo para as armações calculadas:

• 3,15 cm²/m para a negativa na direção do balanço
• 1,00 cm²/m para a negativa na outra direção
• 1,00 cm²/m para a positiva nas duas direções

Utilizando alguma tabela que contenha taxa de aço por metro:

A partir da tabela, utilizaremos barras de 8 mm a cada 15 cm, o que equivale a 4,0 cm²/m para a armação negativa principal e barras de 5 mm a cada 20 cm para as demais armações.

Vale lembrar que a norma ABNT/NBR: 6118 (2014) prescreve um espaçamento máximo para barras da armadura principal de flexão de 20 cm ou duas vezes a espessura da laje.

Abaixo segue um esquema com as armações detalhadas a partir do dimensionamento da marquise:

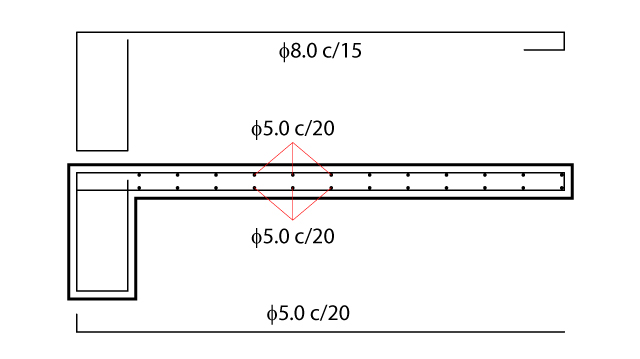
Análise em softwares de cálculo

É importante observar que algumas questão irão influenciar sobre a consideração ou não do nível de engastamento fornecido pelo apoio. Variando, por exemplo, com a rigidez à torção da viga que engasta a marquise.

Softwares comerciais aumentam a produtividade do engenheiro calculista ao realizar essas verificações automáticas, desde que bem configurados.

Esse é o ponto chave na utilização de softwares, o entendimento da utilização da ferramenta para que sejam feitos os ajustes na mesma.

Se você tem interesse em ingressar na área de cálculo estrutural, recomendo bastante o curso Essencial em Concreto Armado do professor Rangel Lage em que você irá aprender a utilizar o software TQS (na minha opinião, o melhor software do mercado) passando por TODAS as etapas (desde a concepção estrutural até elaboração das pranchas) necessárias para o desenvolvimento de um projeto completo.

Considerações finais

Nesse post você aprendeu a calcular os esforços solicitantes e as armações de flexão de marquises. Vale lembrar que ainda devemos verificar os esforços de cisalhamento e os estados limites de serviço, mas isso deixaremos para um próximo post.

Até a próxima!

---

Fonte:

ARAÚJO, J. M. Curso de Concreto Armado. Rio Grande: Editora Dunas, 2014. v. 2.

ASSOCIAÇÃO BRASILEIRA DE NORMAS TÉCNICAS. NBR 6120: Cargas para o cálculo de estruturas de edificações. Rio de Janeiro, 1980.

ASSOCIAÇÃO BRASILEIRA DE NORMAS TÉCNICAS. NBR 6118: Projeto de estruturas de concreto – Procedimento. Rio de Janeiro, 2014.

CARVALHO, R. C.; FIGUEIREDO FILHO, J. R. Cálculo e Detalhamento de Estruturas Usuais de Concreto Armado Segundo a NBR 6118:2014. São Carlos: EdUFSCar, 2014.