Dimensionando vigas submetidas à torção

Nesse post, vou ensinar a você a como verificar uma viga submetida as esforços de torção, desde o cálculo da armação necessária até a verificação das tensões de compressão no concreto. Você ainda terá acesso a um exemplo prático de uma viga engastando uma marquise de concreto armado.

Vamos ao texto!

Introdução

A partir de experimentos com vigas submetidas à torção, pode ser observado que, após o surgimento das fissuras, apenas uma casca de concreto resiste aos esforços de torção.

Dessa forma, a norma brasileira ABNT/NBR: 6118 (2014) fornece, para o dimensionamento de seções solicitadas a torção, algumas expressões para calcular a espessura da parede da seção vazada equivalente.

Geometria da seção vazada equivalente submetida à torção

A obtenção da geometria da seção vazada é obtida a partir das seguintes variáveis:

Área da seção bruta de concreto: \mathrm{A};

perímetro da seção bruta: \mathrm{u};

distância do eixo da armadura longitudinal para a face da seção, \mathrm{C_1}.

Caso \mathrm{\dfrac{A}{u} \geq 2 \cdot C_1}:

\mathrm{h_e = \dfrac{b \cdot h}{2 \cdot (b + h)}}

\mathrm{A_e = (b-h_e) \cdot (h-h_e)}

\mathrm{u_e = 2 \cdot (b+h-2 \cdot h_e)}

Caso \mathrm{\dfrac{A}{u} < 2 \cdot C_1}:

\mathrm{h_e = \dfrac{b \cdot h}{2 \cdot (b + h)} \leq b - 2 \cdot C_1}

\mathrm{A_e = (b- 2 \cdot C_1) \cdot (h- 2 \cdot C_1)}

\mathrm{u_e = 2 \cdot (b+h-4 \cdot C_1)}

Cálculo das armaduras transversais e longitudinais

Baseado na geometria da seção equivalente, conforme realizado para cisalhamento em vigas, utilizaremos uma analogia de treliças, mas dessa vez, uma treliça espacial.

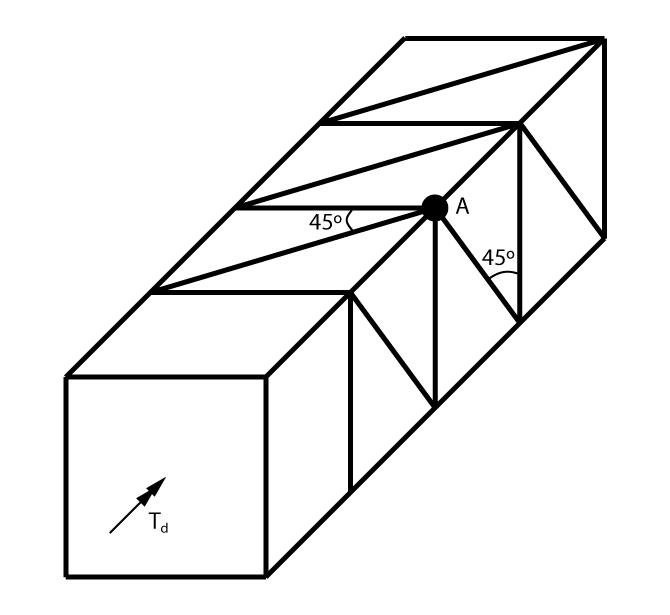
Podemos resolver essa treliça pelo métodos dos nós. Analisando o nó A, concorrem as bielas da face superior e da face lateral, a tração da armadura superior e dos estribos.

Dessa forma, podemos calcular a força atuante na armadura transversal e longitudinal em função da força atuante na biela:

\mathrm{F_{st} = F_c \cdot cos \dfrac{\pi}{4} = \dfrac{F_c}{\sqrt{2}}}

\mathrm{F_{sl} = F_c \cdot cos \dfrac{\pi}{4} = \dfrac{F_c}{\sqrt{2}}}

Realizando um corte transversal A-A e decompondo as quatro bielas seccionadas pelo corte, teremos que a força de cada biela decomposta vale:

\mathrm{F_c \cdot cos \dfrac{\pi}{4} = F_c \cdot \dfrac{\sqrt{2}}{2}}

Com isso, igualando o momento torsor \mathrm{T_d} com o momento gerado pelas quatro bielas decompostas, teremos:

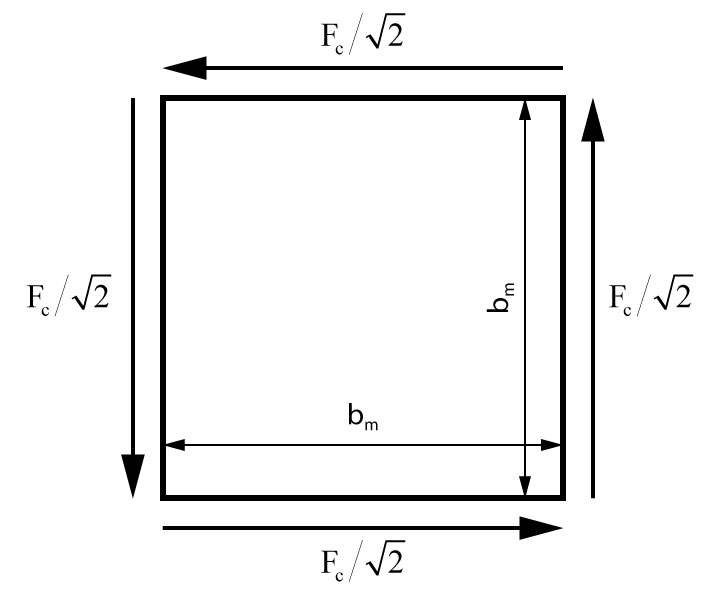
\mathrm{T_d = 4 \cdot F_c \cdot \dfrac{\sqrt{2}}{2} \cdot \dfrac{b_m}{2}}

\mathrm{T_d = 2 \cdot b_m \cdot \dfrac{F_c}{\sqrt{2}}}

Aplicando a fórmula anterior nas expressões de \mathrm{F_{st}} e \mathrm{F_{sl}}, temos:

\mathrm{F_{sl} = F_{st} = \dfrac{T_d}{2 \cdot b_m}}

Armadura transversal

Conforme desenvolvemos para vigas submetidas a esforços de cortantes, na realidade, entre duas bielas utilizaremos um conjunto de estribos:

\mathrm{A_s = \dfrac{b_m}{s} \cdot A_{s1}}

\mathrm{F_{st} = \dfrac{b_m}{s} \cdot A_{s1} \cdot f_{yd} = \dfrac{T_d}{2 \cdot b_m}}

\mathrm{\dfrac{A_{s1}}{s} = \dfrac{T_d}{2 \cdot b_m ^2 \cdot f_{yd}}=\dfrac{T_d}{2 \cdot A_e \cdot f_{yd}}}

A fim de obter uma área de aço por metro, vamos considerar o valor \mathrm{s=100 \; cm}:

\mathrm{A_{sw} = \dfrac{100 \cdot T_d}{2 \cdot A_e \cdot f_{yd}}}, cm²/m

Diferente da forma que obtivemos os estribos para resistir aos esforços cortantes, essa área de aço será utilizada diretamente nas tabelas de área de aço por metro, não sendo necessário, portanto, a divisão pelo número de ramos. Isso ocorre devido ao fato de que a força utilizada para o cálculo dessa área já foi obtida em um único ramo.

Armadura longitudinal

Sabendo que teremos uma força \mathrm{F_{sl}} em cada armadura de canto, é possível obter uma área de aço por unidade de comprimento:

\mathrm{f_{sl} = \dfrac{4 \cdot F_{sl}}{4 \cdot b_m} = \dfrac{F_{sl}}{b_m}}

\mathrm{f_{sl} = \dfrac{T_d}{2 \cdot b_m \cdot b_m} = \dfrac{T_d}{2 \cdot A_e}}

Sabendo que a área de aço necessária é a força atuante sobre a tensão atuante e que a força atuante é a taxa de força por unidade de comprimento multiplicado pelo perímetro, temos:

\mathrm{A_{sl} = \dfrac{f_{sl} \cdot u_e}{f_{yd}} = \dfrac{T_d \cdot u_e}{2 \cdot A_e \cdot f_{yd}}}, cm²

Verificação das tensões na biela

Seguindo a formulação presente na ABNT/NBR: 6118 (2014), a resistência da diagonal comprimida é:

\mathrm{T_{Rd2} = 0,50 \cdot \alpha_v \cdot f_{cd} \cdot A_e \cdot h_e \cdot sen(2 \cdot \theta)}

Sabendo que deve-se utilizar a mesma inclinação de biela tanto para a verificação da cortante quanto para a verificação da torção, e considerando a inclinação da biela de 45º:

\mathrm{T_{Rd2} = 0,50 \cdot \alpha_v \cdot f_{cd} \cdot A_e \cdot h_e}

Levando em consideração o esforço cortante atuando conjuntamente com a torção, a verificação passa a ser:

\mathrm{\dfrac{V_{Sd}}{V_{Rd2}} + \dfrac{T_{Sd}}{T_{Rd2}} \leq 1}

Armações mínimas e detalhamento

Armadura transversal mínima

A armação transversal final é obtida somando as armaduras que foram calculadas separadamente para o esforço de torção e de cisalhamento. Essa armadura deve respeitar a armação mínima:

\mathrm{A_{sw,min} = \rho_{w,min} \cdot 100 \cdot b_w}, cm²/m

Em que \mathrm{\rho_{w,min}} vale \mathrm{0,2 \cdot \dfrac{f_{ct,m}}{f_{ywk}}} e é apresentado na tabela abaixo para o aço CA50.

Espaçamento máximo da armadura transversal

O espaçamento máximo entre estribos irá variar da relação entre \mathrm{V_{Sd}} e \mathrm{V_{Rd2}} e da relação entre \mathrm{T_{Sd}} e \mathrm{T_{Rd2}}:

se \mathrm{\dfrac{V_{Sd}}{V_{Rd2}} + \dfrac{T_{Sd}}{T_{Rd2}}  \leq 0,67}, então \mathrm{s_{máx} = 0,6 \cdot d \leq 300 \; mm}

se \mathrm{\dfrac{V_{Sd}}{V_{Rd2}} + \dfrac{T_{Sd}}{T_{Rd2}}  > 0,67}, então \mathrm{s_{máx} = 0,3 \cdot d \leq 200 \; mm}

Armadura longitudinal mínima

A armadura longitudinal decorrente do esforço de torção, tem o valor mínimo:

\mathrm{A_{sl,min} = \dfrac{\rho_{w,min}}{2} \cdot u_e \cdot b_w}, cm²

Para essa armadura longitudinal, deve-se utilizar barras de bitola no mínimo 10 mm e pelo menos igual a armadura transversal.

No caso de seções retangulares com dimensões iguais ou inferiores a 40 cm, a armadura longitudinal de torção pode se concentrar nos cantos. Caso contrário, a mesma deve ser distribuída ao longo do perímetro da seção.

Exemplo aplicado

Como exemplo, vamos resolver uma viga biapoiada, de 20 cm de largura por 40 cm de altura, utilizada para engastar uma marquise já dimensionada anteriormente. A mesma possui dimensões de 2,6 m por 1,5 m e um carregamento total de 4,0 kN/m² (já incluindo ações permanentes e variáveis).

Caso prefira, você pode conferir esse exercício também pelo vídeo abaixo:

Obtenção dos esforços

Essa marquise foi dimensionada para um momento fletor \mathrm{M_k = 5,12 \; kN \cdot m / m} na região do engaste, o que gera uma solicitação de torção distribuída na viga dos mesmos \mathrm{5,12 \; kN \cdot m / m}.

Sabendo que o comprimento efetivo da viga vale 3,0 m (2,6 + 0,2 + 0,2), o máximo esforço torsor na viga, localizado nos apoios, vale:

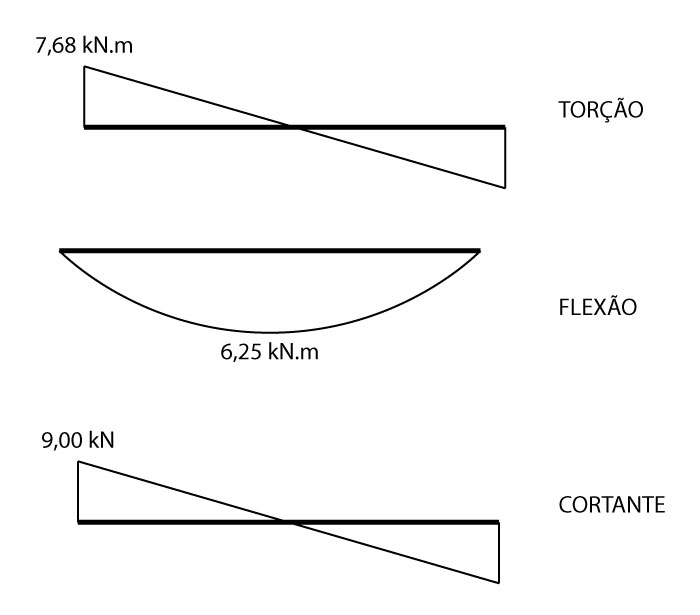
\mathrm{T_{Sk} = \dfrac{5,12 \cdot 3,0}{2} = 7,68 \; kN \cdot m}

O momento fletor e esforço cortante máximos valem:

\mathrm{M_{Sk} = \dfrac{6 \cdot 3^2}{8} = 6,75 \; kN \cdot m}

\mathrm{V_{Sk} = \dfrac{6 \cdot 3}{2} = 9 \; kN}

O resumo dos esforços calculados estão resumidos na figura abaixo:

Geometria da seção equivalente

Calculando inicialmente a área e o perímetro da seção bruta:

\mathrm{A = b \cdot h = 20 \cdot 40}

\mathrm{A = 800 \; cm^2}

\mathrm{u = 2 \cdot (b+h) = 2 \cdot (20+40)}

\mathrm{u = 120 \; cm}

Logo, a razão entre área e perímetro vale:

\mathrm{\dfrac{A}{u} = 6,67 \; cm}

Como \mathrm{\dfrac{A}{u} \geq 2 \cdot C_1 = 5}:

\mathrm{h_e  = 6,67 \; cm}

Calculando agora a área da seção vazada:

\mathrm{A_e  = (b-h_e) \cdot (h-h_e)}

\mathrm{A_e  = (20-6,67) \cdot (40-6,67)}

\mathrm{A_e  = 444,29 cm^2}

E o perímetro da seção vazada:

\mathrm{u_e  = 2 \cdot (b+h-2 \cdot h_e)}

\mathrm{u_e  = 2 \cdot (20+40-2 \cdot 6,67)}

\mathrm{u_e  = 93,32 \; cm}

Armadura transversal

É necessário armadura transversal tanto devido ao esforço cortante quanto devido ao momento torsor. Devido ao momento torsor será necessária uma armadura de:

\mathrm{A_{sw} = \dfrac{100 \cdot T_{Sd}}{2 \cdot A_e \cdot f_{yd}}}

\mathrm{A_{sw} = \dfrac{100 \cdot 1,4 \cdot 768}{2 \cdot 444,29 \cdot 43,5}}

\mathrm{A_{sw} = 2,78 \; cm^2 / m}

Calculando a armadura transversal para resistir ao esforço cortante, como \mathrm{V_c > V_{Sd}}, iremos comparar a área de aço encontrada com a armadura transversal mínima.

\mathrm{A_{sw,min} = \rho_{w,min} \cdot 100 \cdot b_w}

\mathrm{A_{sw,min} = \dfrac{0,09}{100} \cdot 100 \cdot 20}

\mathrm{A_{sw,min} = 1,8 \; cm^2}

Calculando o espaçamento máximo entre os estribos:

\mathrm{T_{Rd2} = 0,50 \cdot \alpha_v \cdot f_{cd} \cdot A_e \cdot h_e}

\mathrm{T_{Rd2} = 0,50 \cdot \left(1- \dfrac{20}{250}\right) \cdot \dfrac{2}{1,4} \cdots}

\mathrm{\cdots \; \cdot 444,29 \cdot 6,67 = 1947,39 \; kN \cdot cm}

\mathrm{\dfrac{V_{Sd}}{V_{Rd2}} + \dfrac{T_{Sd}}{T_{Rd2}}}

\mathrm{\dfrac{12,6}{255,5} + \dfrac{1075,2}{1947,39} = 0,6 \leq 0,67}

Logo, o espaçamento máximo entre os estribos vale:

\mathrm{s_{máx} = 0,6 \cdot d \leq 300 \; mm}

\mathrm{s_{máx} = 0,6 \cdot 36 = 21,6 \; cm}

Utilizando uma tabela que combine diâmetro da barra com espaçamento, temos:

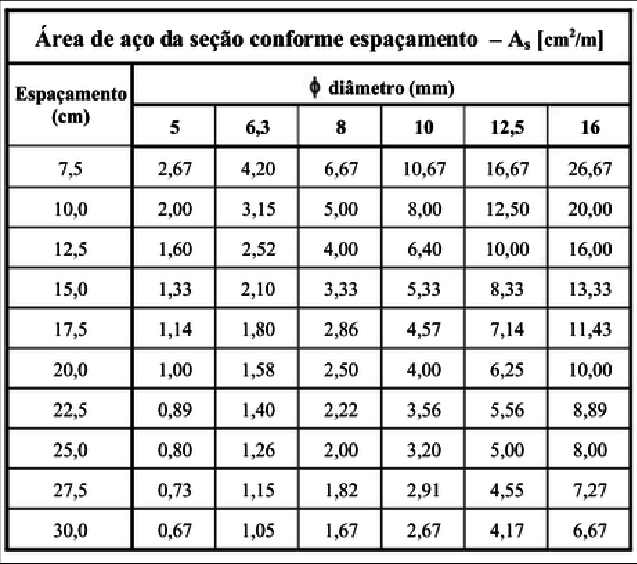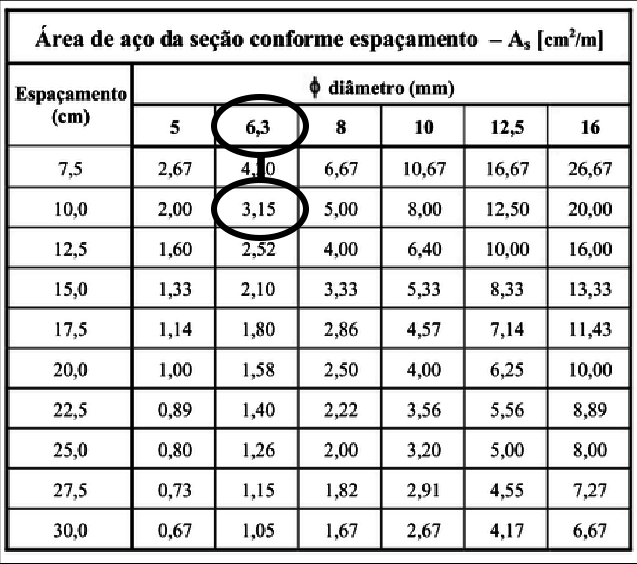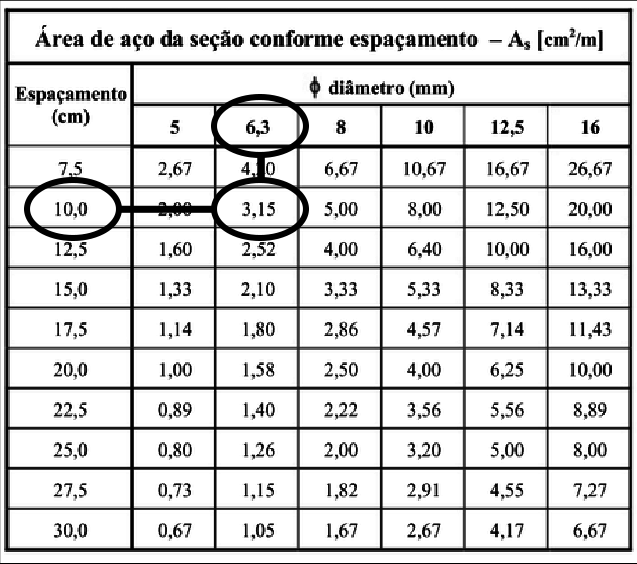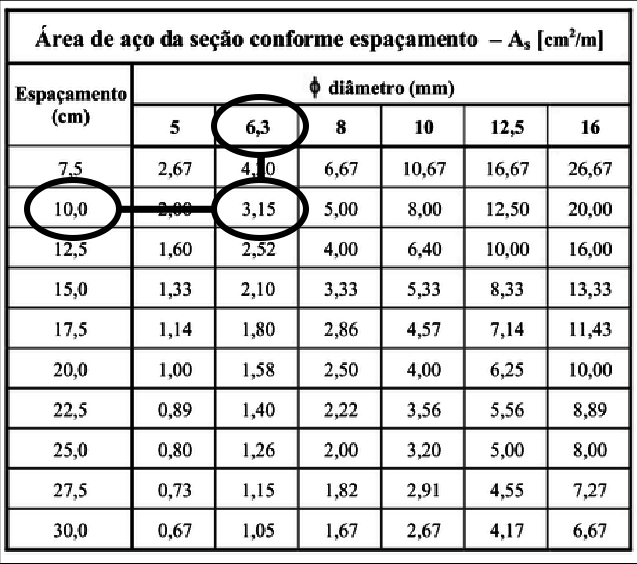
Sendo assim, utilizaremos barras de 6,3 mm a cada 10 cm para resistir a torção combinada com cisalhamento.

Armadura longitudinal

A armadura longitudinal para resistir ao esforço de torção, vale:

\mathrm{A_{sl} = \dfrac{T_d \cdot u_e}{2 \cdot A_e \cdot f_{yd}}}

\mathrm{A_{sl} = \dfrac{1075,2 \cdot 93,32}{2 \cdot 444,29 \cdot 43,5}}

\mathrm{A_{sl} = 2,6 \; cm^2}

A armadura longitudinal mínima para resistir ao esforço de torção, vale:

\mathrm{A_{sl,min} = \dfrac{\rho_{w,min}}{2} \cdot u_e \cdot b_w}

\mathrm{A_{sl,min} = \dfrac{0,09}{2 \cdot 100} \cdot 93,32 \cdot 20}

\mathrm{A_{sl,min} = 0,84 \; cm^2}

O dimensionamento da viga para resistir ao momento fletor vale 0,61 cm².

Será utilizado a armadura de flexão mínima \mathrm{A_{s,min} = \dfrac{0,15}{100} \cdot b_w \cdot h}, que vale 1,2 cm².

Verificação da biela

Para verificação da biela, retomaremos o cálculo realizado anteriormente:

\mathrm{\dfrac{V_{Sd}}{V_{Rd2}} + \dfrac{T_{Sd}}{T_{Rd2}}}

\mathrm{\dfrac{12,6}{255,5} + \dfrac{1075,2}{1947,39} = 0,6 \leq 1,0}

Dessa forma, não haverá esmagamento do concreto.

Detalhamento da seção transversal

Segue abaixo o detalhamento final da seção transversal:

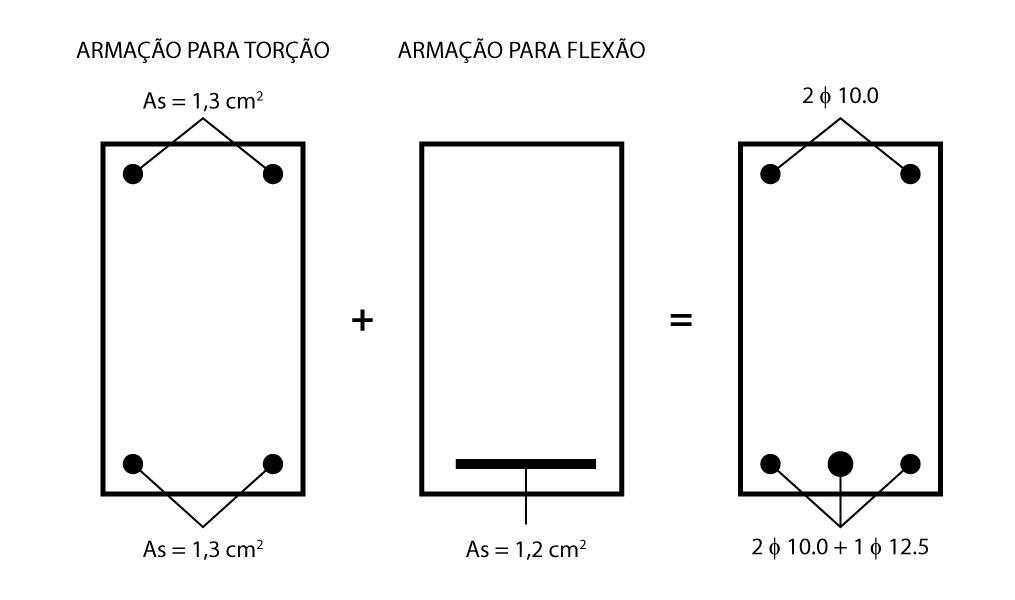
Nesse post você aprendeu a calcular as armaduras necessárias para resistir esforços de torção assim como verificar a tensão nas bielas.

E ai, gostou do post? Coloca ai suas dúvidas e sugestões nos comentários!

---

Fonte:

ARAÚJO, J. M. DE. Dimensionamento à torção de vigas de concreto armado. Teoria e Prática na Engenharia Civil, n. 21, p. 1–11, 2013.

ARAÚJO, J. M. Curso de Concreto Armado. Rio Grande: Editora Dunas, 2014. v. 4

ASSOCIAÇÃO BRASILEIRA DE NORMAS TÉCNICAS. NBR 6118: Projeto de estruturas de concreto – Procedimento. Rio de Janeiro, 2014.

BASTOS, P. S. DOS S. Apostila: Torção em vigas de concreto armado. Bauru, 2015.