Verificando o cisalhamento em vigas de concreto

Não conhece os dois modelos de cálculo previstos na norma brasileira para verificação de cisalhamento em vigas de concreto? Não entende o sentido físico das formulações de cisalhamento presente na norma? Nesse texto, além de dimensionar e verificar uma viga de concreto armado para os esforços cortantes solicitantes, você irá entender o real sentido das equações presentes na norma brasileira e nos livros didáticos.

Desenvolvimento teórico

O modelo de bielas e tirantes é uma abordagem muito utilizada para representar estruturas fissuradas de concreto armado. Esse modelo consiste em representar a estrutura por meio de uma treliça equivalente.

Essa abordagem se justifica pelo fato do concreto armado carregar ações através de campos de tensões de compressão (denominados de biela), distribuídos e interligados por tirantes tracionados, normalmente sendo utilizado barras de aço.

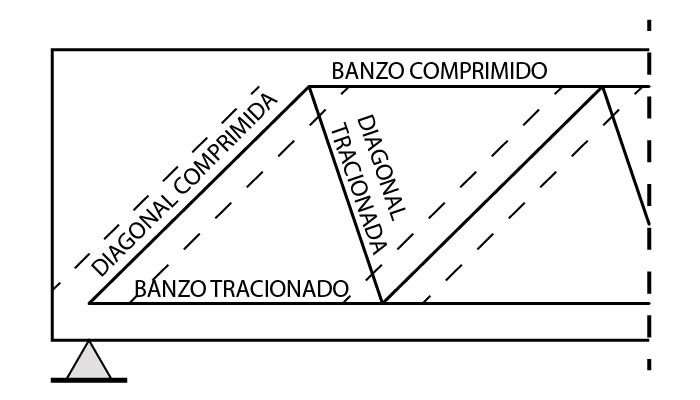
A ABNT/NBR: 6118 (2014) utiliza a analogia de treliças para verificação e dimensionamento do cisalhamento em vigas de concreto. Analisando conforme o modelo de bielas e tirantes devemos basicamente verificar o concreto solicitado à compressão e dimensionar as barras de aço solicitadas a tração.

Considerando um trecho submetido a um esforço cortante de cálculo \mathrm{V_{Sd}}, braço de alavanca Z, inclinação das bielas \mathrm{\theta} e inclinação dos tirantes (estribos) \mathrm{\alpha}:

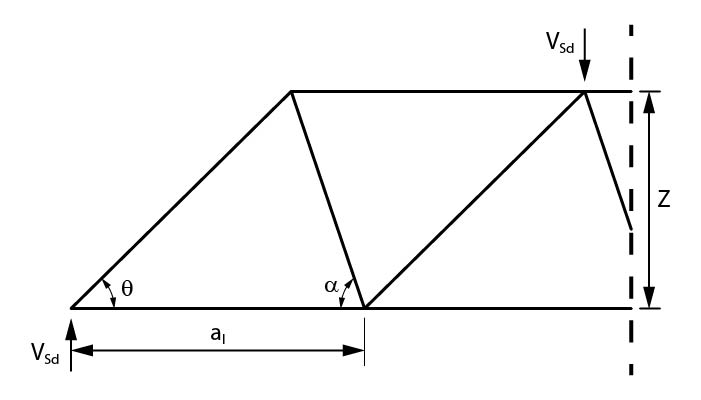
É possível obter, apenas por trigonometria simples, a distância \mathrm{a_l} entre duas bielas:

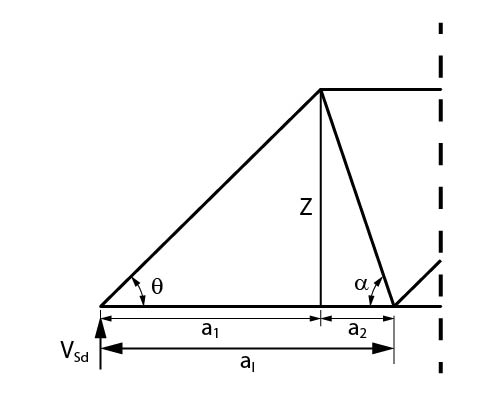
\mathrm{tg \theta=\dfrac{Z}{a_1} \rightarrow a_1 = Z \cdot cotg \theta}

\mathrm{tg \alpha=\dfrac{Z}{a_2} \rightarrow a_2 = Z \cdot cotg \alpha}

\mathrm{a_l = a_1 + a_2 = Z \cdot cotg \theta + Z \cdot cotg \alpha}

\mathrm{a_l = Z \cdot ( cotg \theta + cotg \alpha)}

Podemos resolver essa região da treliça através do método de Ritter (ou seccional) ao traçarmos duas seções:

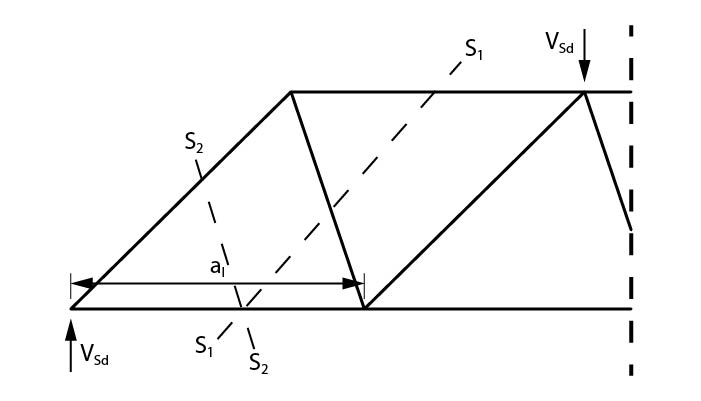
Analisando inicialmente a seção S1 é possível obter o esforço aplicado no tirante:

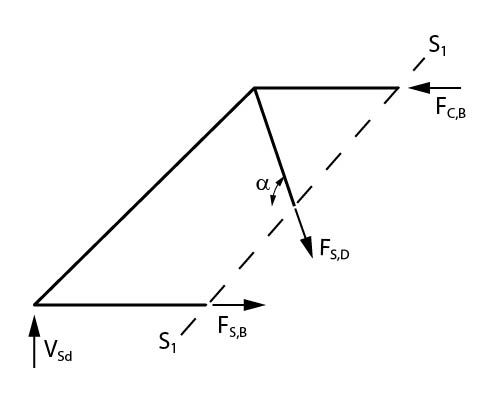
\mathrm{F_{S,D} \cdot sen \alpha = V_{Sd}}

\mathrm{F_{S,D}=\dfrac{V_{Sd}}{sen \alpha}}

De forma análoga, utilizando a seção S2, podemos calcular a compressão que atua na biela:

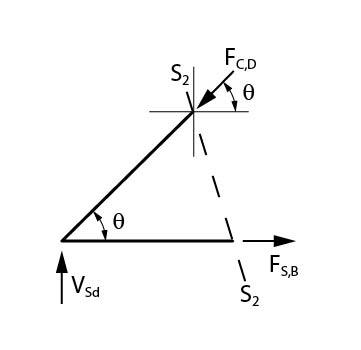
\mathrm{F_{C,D} \cdot sen \theta= V_{Sd}}

\mathrm{F_{C,D}=\dfrac{V_{Sd}}{sen \theta}}

Verificação da biela (diagonal comprimida)

Sabendo a dimensão entre duas bielas sucessivas é possível obter a distância entre duas bielas:

\mathrm{sen \theta = \dfrac{a_l '}{a_l} \rightarrow a_l ' = a_l \cdot sen \theta}

Com esse valor podemos calcular a área perpendicular à biela apenas multiplicando-o pela largura da peça:

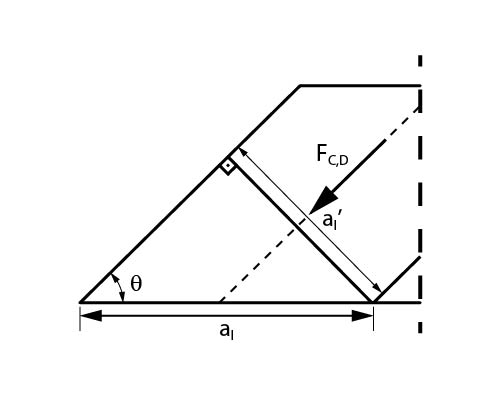
\mathrm{A_c = a_l ' \cdot b_w = a_l \cdot sen \theta \cdot b_w}

Logo, podemos calcular a tensão na biela:

\mathrm{\sigma _C = \dfrac{F_{C,D}}{A_c}}

\mathrm{\sigma _C = \dfrac{V_{Sd}}{b_w \cdot Z \cdot (cotg \theta + cotg \alpha) \cdot sen^2 \theta}}

Realizando a aproximação \mathrm{Z=0,9 \cdot d}, chegamos a seguinte formulação:

\mathrm{\sigma _C = \dfrac{1,11 \cdot V_{Sd}}{b_w \cdot d \cdot(cotg \theta + cotg \alpha) \cdot sen^2 \theta}}

De acordo com a CEB/90 a tensão atuante nessa biela deve ser limitada a:

\mathrm{0,6 \cdot \left( 1 - \dfrac{f_{ck}}{250} \right) \cdot f_{cd} = 0,6 \cdot \alpha_v \cdot f_{cd}}

Logo:

\mathrm{\sigma_c \leq 0,6 \cdot \alpha_v \cdot f_{cd}}

Isolando agora \mathrm{V_{Sd}}:

\mathrm{V_{Sd} \leq 0,54 \cdot \alpha_v \cdot f_{cd} \cdots}

\mathrm{\cdot (cotg \theta + cotg \alpha) \cdot sen ^2 \theta \cdot b_w \cdot d}

Dimensionamento do estribo

Sabendo que o espaçamento entre duas bielas é \mathrm{a_l}, devemos utilizar um espaçamento de estribos \mathrm{s}, inferior a \mathrm{a_l}, a fim de garantir que a fissura seja interceptada por um estribo.

Desse modo, a quantidade de estribos entre duas bielas é:

\mathrm{n = \dfrac{a_l}{s}}

E a área de aço total dos estribos entre duas bielas é:

\mathrm{A_s = n \cdot A_{s1} = \dfrac{a_l}{s} \cdot A_{s1}}

Assumindo que todos os estribos escoaram, podemos calcular a força atuante nesse tirante:

\mathrm{F = A_s \cdot f_{yd} = \dfrac{a_l}{s} \cdot A_{s1}\cdot f_{yd}}

Igualando a força calculada acima com a força nos tirantes obtida geometricamente no início do desenvolvimento e utilizando as considerações de Z:

\mathrm{\dfrac{a_l}{s} \cdot A_{s1}\cdot f_{yd} = \dfrac{V_{Sd}}{sen \alpha}}

\mathrm{\dfrac{A_{s1}}{s} = \dfrac{V_{Sd}}{a_l \cdot f_{yd} \cdot sen \alpha}}

\mathrm{\dfrac{A_{s1}}{s} = \dfrac{V_{Sd}}{Z \cdot (cotg \theta + cotg \alpha) \cdot f_{yd} \cdot sen \alpha}}

\mathrm{\dfrac{A_{s1}}{s} = \dfrac{1,11 \cdot V_{Sd}}{d \cdot (cotg \theta + cotg \alpha) \cdot f_{yd} \cdot sen \alpha}}

Utilizando \mathrm{s = 100 \; cm} para obtermos o resultado em \mathrm{cm^2 / m}:

\mathrm{A_{sw} = \dfrac{111 \cdot V_{Sd}}{d \cdot (cotg \theta + cotg \alpha) \cdot f_{yd} \cdot sen \alpha}}

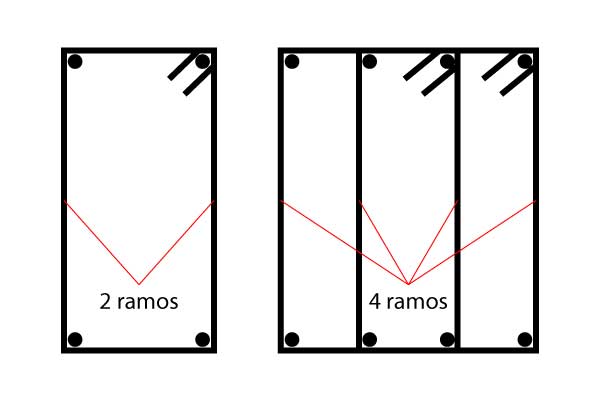
Como a formulação sai em cm²/m, podemos utilizar qualquer tabela que converta área de aço por metro em bitola por espaçamento. É importante lembrar que essa armação de cisalhamento ainda será divida pela quantidade de ramos que o estribo possui. Usualmente, as vigas são armadas com estribos simples (com dois ramos). Em algumas situações, como vigas alavanca, há necessidade de utilizar estribo duplo (com quatro ramos).

Considerações da norma ABNT/NBR: 6118 (2014) para verificação de cisalhamento em vigas

Alguns efeitos, como a contribuição do concreto tracionado entre as fissuras, o efeito de engrenamento entre os agregados graúdos, o efeito de pino das armaduras longitudinais e o fato do banzo comprimido ser inclinado e não horizontal, não são considerados no modelo de treliça. Fato que gera uma armadura excessiva ao utilizar o dimensionamento acima obtido.

Uma forma de considerar isso é subtrair do valor de \mathrm{V_{Sd}} um \mathrm{V_c} que simboliza a parcela de esforço absorvida por mecanismos complementares a treliça.

A norma considera a utilização de dois modelos de cálculo. Apesar de ambos os modelos permitirem estribos com inclinação de 45º a 90º, por questões práticas, utilizaremos estribos verticais.

Modelo de cálculo I

Esse modelo considera as bielas fixas em 45º em relação ao eixo longitudinal e admite que a parcela \mathrm{V_c} seja constante, independentemente de \mathrm{V_{Sd}}.

Considerando então \mathrm{\theta = \dfrac{\pi}{4}} e assumindo estribos verticais \mathrm{\alpha = \dfrac{\pi}{2}}, a verificação da diagonal comprimida fica:

\mathrm{V_{Sd} \leq 0,54 \cdot \alpha_v \cdot f_{cd} \cdots}

\mathrm{\cdot (cotg \dfrac{\pi}{4} + cotg \dfrac{\pi}{2}) \cdot sen ^2 \dfrac{\pi}{4} \cdot b_w \cdot d}

\mathrm{V_{Sd} \leq V_{Rd2}}

\mathrm{V_{Rd2} = 0,27 \cdot \alpha_v \cdot f_{cd} \cdot b_w \cdot d}

O dimensionamento do estribo pode ser feito por:

\mathrm{A_{sw} = \dfrac{111 \cdot (V_{Sd} - V_c)}{d \cdot (cotg \dfrac{\pi}{4} + cotg \dfrac{\pi}{2}) \cdot f_{yd} \cdot sen \dfrac{\pi}{2}}}

\mathrm{A_{sw} = \dfrac{111 \cdot (V_{Sd} - V_c)}{d \cdot f_{yd}}}

A parcela \mathrm{V_c} varia de acordo com o tipo de solicitação da seção. Para seções submetidas a flexão simples (caso predominante em vigas), pode ser calculada pela formulação abaixo:

\mathrm{V_c = V_{c0} = 0,6 \cdot f_{ctd} \cdot b_w \cdot d}

Considerando o fator de minoração de resistência igual a 1,4 e concreto de até 50 MPa:

\mathrm{V_c = 0,09 \cdot f_{ck} ^{\frac{2}{3}} \cdot b_w \cdot d}

Modelo de cálculo II

O segundo modelo presente na norma para verificação do cisalhamento em elementos lineares considera que as bielas podem variar de 30º a 45º em relação ao eixo longitudinal e admite que a parcela \mathrm{V_c} sofre redução com o aumento de \mathrm{V_{Sd}}.

A verificação da diagonal comprimida é dada por:

\mathrm{V_{Sd} \leq 0,54 \cdot \alpha_v \cdot f_{cd} \cdots}

\mathrm{\cdot (cotg \theta + cotg \dfrac{\pi}{2}) \cdot sen ^2 \theta \cdot b_w \cdot d}

\mathrm{V_{Sd} \leq 0,54 \cdot \alpha_v \cdot f_{cd} \cdots}

\mathrm{\cdot cotg \theta \cdot sen ^2 \theta \cdot b_w \cdot d = V_{Rd2}}

Para o dimensionamento dos estribos:

\mathrm{A_{sw} = \dfrac{111 \cdot (V_{Sd} - V_c)}{d \cdot (cotg \theta + cotg \dfrac{\pi}{2}) \cdot f_{yd} \cdot sen \dfrac{\pi}{2}}}

\mathrm{A_{sw} = \dfrac{111 \cdot (V_{Sd} - V_c)}{d \cdot cotg \theta \cdot f_{yd}}}

A parcela \mathrm{V_c} para seções submetidas a flexão simples pode ser calculada por:

\mathrm{V_c = V_{c0} = 0,09 \cdot f_{ck} ^ \frac{2}{3} \cdot b_w \cdot d}, se \mathrm{V_{Sd} \leq V_{c0}};

\mathrm{V_c = 0}, se \mathrm{V_{Sd} = V_{Rd2}}.

Para valores intermediários, deve-se interpolar linearmente, conforme ilustrado na figura abaixo:

Armações transversais mínimas

No caso de vigas, mesmo para \mathrm{V_{Sd} \leq V_c}, é necessário dispor de uma armadura transversal mínima. Essa armadura, no caso de estribos verticais, pode ser calculada pela expressão abaixo:

\mathrm{A_{sw,min} = \rho_{w,min} \cdot 100 \cdot b_w}, cm²/m

Em que \mathrm{\rho_{w,min}} vale \mathrm{0,2 \cdot \dfrac{f_{ct,m}}{f_{ywk}}} e é apresentado na tabela abaixo para o aço CA50.

A tabela apresentada acima é valida tanto para aço CA50 quanto para aço CA60, uma vez que a norma considera que para o dimensionamento de estribos nas vigas o máximo valor do fyd seja 435 MPa.

O espaçamento máximo entre estribos irá variar da relação entre \mathrm{V_{Sd}} e \mathrm{V_{Rd2}}:

se \mathrm{V_{Sd} \leq 0,67 \cdot V_{Rd2}}, então \mathrm{s_{máx} = 0,6 \cdot d \leq 300 \; mm}

se \mathrm{V_{Sd} > 0,67 \cdot V_{Rd2}}, então \mathrm{s_{máx} = 0,3 \cdot d \leq 200 \; mm}

O máximo espaçamento entre ramos sucessivos de um mesmo estribo também é limitado pela relação entre \mathrm{V_{Sd}} e \mathrm{V_{Rd2}}:

se \mathrm{V_{Sd} \leq 0,20 \cdot V_{Rd2}}, então \mathrm{s_{t,máx} = d \leq 800 \; mm}

se \mathrm{V_{Sd} > 0,20 \cdot V_{Rd2}}, então \mathrm{s_{t,máx} = 0,6 \cdot d \leq 350 \; mm}

Exemplo aplicado

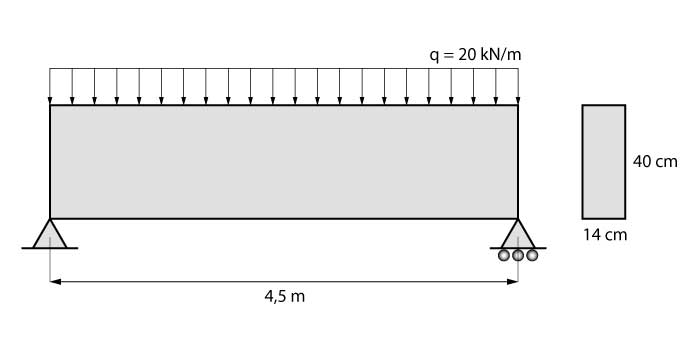
A viga de concreto estudada vence um vão de 4,5 m, possui uma seção de 14 cm de largura por 40 cm de altura, com concreto de 20 MPa, estribos de aço CA60 está submetida a uma carregamento distribuído de 20 kN/m. Para esse exemplo, queremos verificar o cisalhamento: verificar a diagonal comprimida e calcular a área de aço transversal.

 Resolução pelo modelo I

Você pode acompanhar a resolução pelo modelo I assistindo o vídeo abaixo ou simplesmente acompanhando a leitura do post!

Agora, vamos à questão:

Inicialmente é necessário calcular o esforço cortante solicitante, que será utilizado nos dois modelos:

\mathrm{V_{Sd}=\dfrac{1,4 \cdot 20 \cdot 4,5}{2} = 63 \; kN}

Verificando agora a diagonal comprimida:

\mathrm{V_{Rd2}= 0,27 \cdot \left(1-\dfrac{f_{ck}}{250}\right) \cdot f_{cd} \cdot b_w \cdot d}

\mathrm{V_{Rd2}= 0,27 \cdot \left(1-\dfrac{20}{250}\right) \cdot \dfrac{2}{1,4} \cdot 14 \cdot 36}

\mathrm{V_{Rd2}= 178,8 \; kN}

\mathrm{V_{Sd} \leq V_{Rd2}}, logo a diagonal comprimida está verificada

Calculando agora a parcela do cisalhamento resistido por mecanismo complementares a treliça e a armadura transversal:

\mathrm{V_c = 0,09 \cdot f_{ck} ^{\frac{2}{3}} \cdot b_w \cdot d}

\mathrm{V_c = 0,09 \cdot \dfrac{20 ^{\frac{2}{3}}}{10} \cdot 14 \cdot 36}

\mathrm{V_c = 33,4 \; kN}

\mathrm{A_{sw} = \dfrac{111 \cdot (V_{Sd} - V_c)}{d \cdot f_{yd}}}

\mathrm{A_{sw} = \dfrac{111 \cdot (63 - 33,4)}{36 \cdot 43,5}}

\mathrm{A_{sw} = 2,1 \; cm^2 / m}

Calculando agora a armadura mínima de cisalhamento na viga:

\mathrm{A_{sw,min} = \rho_{w,min} \cdot 100 \cdot b_w}

\mathrm{A_{sw,min} = \dfrac{0,09}{100} \cdot 100 \cdot 14 = 1,26 \; cm^2 / m}

Como \mathrm{V_{Sd} \leq 0,67 \cdot V_{Rd2}}, o espaçamento máximo dos estribos vale:

\mathrm{0,6 \cdot d = 0,6 \cdot 36 = 21,6}, arredondado para 20 cm

Como \mathrm{V_{Sd} > 0,20 \cdot V_{Rd2}}, o espaçamento máximo entre os ramos vale:

\mathrm{0,6 \cdot d = 0,6 \cdot 36 = 21,6}

Como a largura total de nossa viga é 14 cm, temos a certeza que o espaçamento entre os dois ramos de um estribo simples é inferior aos 21,6 cm.

Já que estamos utilizando estribo com dois ramos, iremos o par bitola e espaçamento que resulte em uma área de aço igual ou superior a \mathrm{\dfrac{2,1}{2} = 1,05 \; cm^2 / m}:

Sendo assim, utilizaremos barras de 5 mm a cada 17,5 cm para resistir ao esforço cortante.

Resolução pelo modelo II

Caso prefira, você pode acompanhar a resolução pelo modelo II através do vídeo abaixo.

Resolvendo a mesma viga agora para o modelo II, podemos variar a inclinação da biela de 30º a 45º. Nesse exemplo, consideraremos uma biela inclinada 30º em relação a longitudinal.

Verificando inicialmente a diagonal comprimida:

\mathrm{V_{Rd2} = 0,54 \cdot \alpha_v \cdot f_{cd} \cdots}

\mathrm{\cdot cotg \theta \cdot sen ^2 \theta \cdot b_w \cdot d}

\mathrm{V_{Rd2} = 0,54 \cdot \left(1-\dfrac{20}{250}\right) \cdot \dfrac{2}{1,4} \cdots}

\mathrm{\cdot cotg \dfrac{\pi}{6} \cdot sen ^2 \dfrac{\pi}{6} \cdot 14 \cdot 36}

\mathrm{V_{Rd2} = 154,9 \; kN}

\mathrm{V_{Sd} \leq V_{Rd2}}, logo a diagonal comprimida está verificada

Obtendo a parcela de esforço resistida por mecanismo complementares a treliça:

Como o esforço cortante  de cálculo é superior a \mathrm{V_{c0}} (vide resolução pelo modelo I) e inferior \mathrm{V_{Rd2}} é necessário interpolar para obter o valor de \mathrm{V_c}:

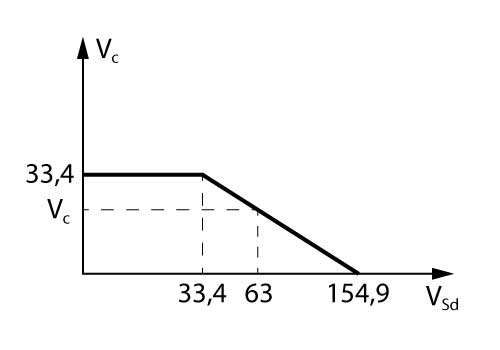
\mathrm{V_c = 33,4 - \dfrac{63 - 33,4}{154,9-33,4} \cdot 33,4}

\mathrm{V_c = 25,3 kN}

Por fim, vamos calcular a área de aço necessária para cisalhamento:

\mathrm{A_{sw} = \dfrac{111 \cdot (V_{Sd} - V_c)}{d \cdot cotg \theta \cdot f_{yd}}}

\mathrm{A_{sw} = \dfrac{111 \cdot (63 - 25,3)}{36 \cdot cotg \dfrac{\pi}{6} \cdot 43,5}}

\mathrm{A_{sw} = 1,54 \; cm^2}

Utilizando a mesma tabela de área de aço por metro e procurando o valor de \mathrm{\dfrac{1,54}{2} = 0,77 \; cm^2 / m}, podemos utilizar barras de 5 mm a cada 20 cm, estando limitado pelo espaçamento máximo entre estribos.

E ai, conseguiu entender bem como dimensionar e verificar cisalhamento em vigas de concreto? Deixa ai nos comentários suas dúvidas e sugestões para posts futuros.

José de Moura

Gostaria de ter acesso a um curso sobre modelagem de alvenaria estrutural no Revit?

Aproveite enquanto está com um preço especial.

carnotengenharia.com.br/