Dimensionamento de vigas: cálculo da armação

Uma vez que você já conhece as hipóteses de calculo por trás do dimensionamento de seções submetidas à flexão, podemos avançar para a obtenção das equações em si. Nessa publicação você aprenderá como obter as equações para o cálculo da posição da linha neutra e da armação de flexão a ser adicionada à seção a fim de resistir ao momento solicitante.

Equacionamento para cálculo da área de aço

Antes de mais nada, nas deduções a seguir vamos considerar apenas o caso de concretos de até 50 MPa. Caso queira, lembrar as diferenças para os concretos com a resistência característica acima de 50 MPa basta conferir a publicação sobre hipóteses de cálculo.

Equilíbrio da seção para o dimensionamento

Primeiramente, vamos garantir o equilíbrio da seção transversal. A fim de alcançarmos isso, iremos igualar os momentos fletores e esforços normais externos aos momentos e forças internos à seção.

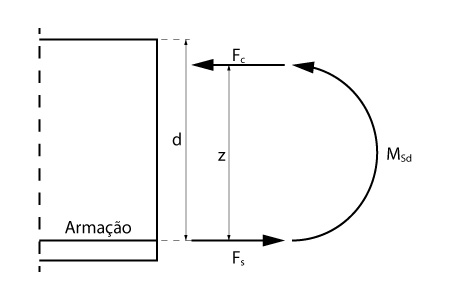
Vamos considerar uma seção submetida à flexão simples, ou seja, sem a presença de forças normais externas. Assim sendo, a força de compressão atuante no concreto deve ser igual a força de tração atuante na armação.

\mathrm{\sum N = 0 \rightarrow F_c = F_s}

Similarmente, o momento solicitante de cálculo \mathrm{M_{Sd}} deve ser igual ao momento gerado pelo binário força no concreto e força na armação.

\mathrm{\sum M = M_{Sd} \rightarrow M_{Sd} = F_c \cdot z}

Cálculo da linha neutra

Conforme apontado nas hipóteses de dimensionamento, apesar da distribuição de tensões de compressão no concreto ser no formato parábola-retângulo, iremos considerar um diagrama retangular com a tensão constate de \mathrm{0,85 \cdot f_{cd}}, distribuído até uma altura de \mathrm{0,8 \cdot x}.

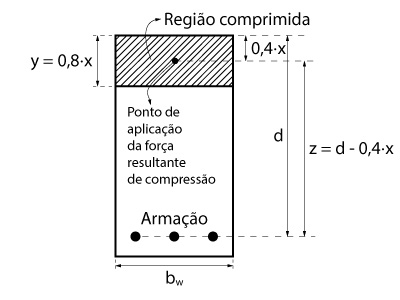
Dessa forma, a área de concreto comprimida vale \mathrm{b_w \cdot 0,8 \cdot x} e para calcular a força de compressão basta multiplicar essa área pela tensão, agora uniforme, de \mathrm{0,85 \cdot f_{cd}}.

\mathrm{F_c = b_w \cdot 0,8 \cdot x \cdot 0,85 \cdot f_{cd}}

\mathrm{F_c = 0,68 \cdot b_w \cdot x \cdot f_{cd}}

Visto que a tensão de compressão é considerada agora como uniforme, o ponto de aplicação da força de resultante recém calculada será aplicada no ponto médio do bloco de tensões (distante \mathrm{0,4 \cdot x} da borda comprimida). Sendo assim, o braço de alavanca \mathrm{z} pode ser calculado por \mathrm{z = d- 0,4 \cdot x}.

Ao retornarmos ao equilíbrio dos momentos, teremos:

\mathrm{M_{Sd} = F_c \cdot z}

\mathrm{M_{Sd} = 0,68 \cdot b_w \cdot x \cdot f_{cd} \cdot (d- 0,4 \cdot x)}

Logo após, podemos rearranjar a equação acima da seguinte forma:

\mathrm{\dfrac{M_{Sd}}{b_w \cdot f_{cd}}  = -0,272 \cdot x^2 + 0,68 \cdot d \cdot x}

É possível organizar a equação acima em um formato conhecido de equação do segundo grau \mathrm{a \cdot x^2 + b \cdot x + c = 0}.

\mathrm{0,272 \cdot x^2 - 0,68 \cdot d \cdot x + \dfrac{M_{Sd}}{b_w \cdot f_{cd}} = 0}

Com o propósito de simplificar, podemos fazer \mathrm{k=\dfrac{M_{Sd}}{b_w \cdot f_{cd}}} e resolver essa equação do segundo grau em função de \mathrm{x}, a fim de obtermos a posição da linha neutra:

\mathrm{x = \dfrac{0,68 \cdot d \pm \sqrt{(-0,68 \cdot d)^2 - 4 \cdot 0,272 \cdot k}}{2 \cdot 0,272}}

\mathrm{x = \dfrac{0,68 \cdot d \pm \sqrt{0,4624 \cdot d^2 - 1,088 \cdot k}}{0,544}}

Cálculo da área de aço

Em segundo lugar, após o cálculo da altura da linha neutra, podemos calcular o valor do braço de alavanca \mathrm{z = d - 0,4 \cdot x}. Já que \mathrm{F_c = F_s}, temos:

\mathrm{M_{Sd} = F_s \cdot z}

Em seguida, podemos substituir a força na armadura pelo produto da área de aço pela tensão:

\mathrm{M_{Sd} = (A_s \cdot f_s) \cdot z}

\mathrm{A_s =\dfrac{M_{Sd}}{z \cdot f_s}}

Caso ainda tenha dúvidas sobre os domínios de dimensionamento, separei um vídeo para você que explica passo a passo a utilização dos domínios de deformação no cálculo de vigas de concreto:

Para os domínios 2 e 3, em que a deformação do aço é superior a deformação de escoamento, a tensão no aço é igual a tensão de escoamento do mesmo. Dessa forma:

\mathrm{f_s = f_{yd}}

\mathrm{A_s =\dfrac{M_{Sd}}{z \cdot f_{yd}}}

Exemplo aplicado sobre dimensionamento de vigas

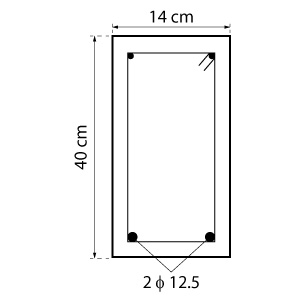
A fim de aplicarmos o que aprendemos até então, vamos resolver uma viga de 14 cm de largura por 40 cm de altura submetida a um momento fletor característico positivo (traciona a borda inferior da viga) \mathrm{M_{Sk} = 20 \; kN \cdot m}. Será considerado um concreto de 20 MPa, aço CA50 (\mathrm{f_{yk} = 500 \; MPa}) e um cobrimento de 2,5 cm.

Caso prefira, você pode acompanhar também a resolução das questões através do vídeo abaixo!

Primeiramente, vamos obter o momento fletor de cálculo para essa viga:

\mathrm{M_{Sd}=\gamma_f \cdot M_{Sk}}

\mathrm{M_{Sd}=1,4 \cdot 20 = 28 \; kN \cdot m}

Com o propósito de calcularmos a altura útil para a viga, vamos considerar barras de 12,5 mm para a armadura longitudinal e estribos de 5,0 mm:

\mathrm{d = h - c - \phi_t - \dfrac{\phi}{2}}

\mathrm{d = 40 - 2,5 - 0,5 - \dfrac{1,25}{2} = 36,4 \; cm}

Cálculo da posição linha neutra

Em seguida, através da equação apresentada anteriormente, podemos calcular agora a posição da linha neutra:

\mathrm{k=\dfrac{M_{Sd}}{b_w \cdot f_{cd}} =\dfrac{2800}{14 \cdot \dfrac{2}{1,4}} = 140 \; cm^2}

\mathrm{x = \dfrac{0,68 \cdot d \pm \sqrt{0,4624 \cdot d^2 - 1,088 \cdot k}}{0,544}}

\mathrm{\dfrac{24,75 \pm \sqrt{0,4624 \cdot (36,4)^2 - 152,3}}{0,544}}

\mathrm { x = \left\{ \begin{array}{ll} 84,9 \; cm \\ 6,1 \; cm \end{array} \right. }

Visto que o exemplo se trata de uma viga submetida à flexão simples (sem presença de esforços normais), não seria possível uma linha neutra que não cortasse a seção. Assim sendo, o resultado \mathrm{x = 84,9} \; cm pode ser descartado.

Uma vez que o limite da linha neutra do domínio 2 vale \mathrm{x_2 = 0,259 \cdot d = 9,4 \; cm} e a linha neutra encontrada (\mathrm{x = 6,1 \; cm}) foi inferior a esse valor, a ruptura no Estado Limite Último é dada no domínio 2.

Cálculo da área de aço

Já que conhecemos agora a profundidade da linha neutra, é possível então determinar o valor do braço de alavanca:

\mathrm{z = d - 0,4 \cdot x}

\mathrm{z = 36,4 - 0,4 \cdot 6,1 = 33,9 \; cm}

Visto que a seção encontra-se no domínio 2, a tensão atuante na armação é igual a tensão de escoamento da mesma. No caso, como estamos utilizando aço CA50, a tensão de escoamento característica e de cálculo valem:

\mathrm{f_{yk} = 500 \; MPa = 50 \; kN/cm^2}

\mathrm{f_{yd} = \dfrac{f_{yk}}{\gamma_s} = \dfrac{50}{1,15} = 43,5 \; kN/cm^2}

Em seguida, em posse do valor do braço de alavanca e da tensão atuante na armação (que no caso é igual a tensão de escoamento) podemos calcular a área de aço necessária:

\mathrm{A_s =\dfrac{M_{Sd}}{z \cdot f_{yd}}}

\mathrm{A_s =\dfrac{2800}{33,9 \cdot 43,5} = 1,9 \; cm^2}

Nós podemos confirmar o resultado encontrado utilizando a nossa Calculadora de Vigas:

[formulario-calculadora-flexao]

Por fim, após o dimensionamento da área de aço necessária, o próximo passo será desenvolver o detalhamento da seção transversal para a viga em questão.

Recado final sobre dimensionamento de vigas

Se você se interessou por esse conteúdo, quero convidar você para conferir o curso Essencial em Concreto Armado do professor Rangel Lage em que você irá aprender a utilizar o software TQS (na minha opinião, o melhor software do mercado) passando por TODAS as etapas (desde a concepção estrutural até elaboração das pranchas) necessárias para o desenvolvimento de um projeto completo.

Nessa publicação você aprendeu como realizar o dimensionamento de uma viga de concreto armado submetida à flexão simples.

---

Fonte:

ARAÚJO, J. M. Curso de Concreto Armado. Rio Grande: Editora Dunas, 2014. v. 1

ASSOCIAÇÃO BRASILEIRA DE NORMAS TÉCNICAS. NBR 6118: Projeto de estruturas de concreto – Procedimento. Rio de Janeiro, 2014.

CARVALHO, R. C.; FIGUEIREDO FILHO, J. R. Cálculo e Detalhamento de Estruturas Usuais de Concreto Armado Segundo a NBR 6118:2014. São Carlos: EdUFSCar, 2014.