Para começarmos, superelevação nada mais é do que a inclinação da seção transversal de uma pista de rolamento (em relação ao eixo da estrada), geralmente expressa em % ou m/m.
Mas para que serve essa inclinação?
Bom, como já vimos nos posts anteriores sobre curva simples e curva com transição, quando um veículo entra em um trajetória curva, ele passa a sentir os efeitos da força centrífuga, que age no sentido de dentro para fora da curva, dificultando a realização do percurso.
Dessa forma, utilizamos a superelevação para contrabalancear a força centrífuga e os esforços laterais, de modo a auxiliar o veículo a realizar a curva de maneira mais confortável e segura.
Pois bem engenheiros, neste post, iremos aprender a calcular a superelevação de uma estrada para os dois tipos de curva horizontal.
Então, antes de mais nada, recomendo que dê uma rápida olhada nos nossos posts de curva horizontal.
Agora, vamos lá?
Quando dispensar a superelevação
Acabamos de descobrir que a superelevação é usada em curvas horizontais para melhorar as condições de movimento do veículo.
No entanto, para curvas com raio muito grande em relação à velocidade diretriz de projeto, os efeitos da força centrífuga são tão pequenos que podem dispensar a necessidade da superelevação.
Para esta situação, então, é admitido apenas o abaulamento normal da pista para evitar possíveis acúmulos de água.
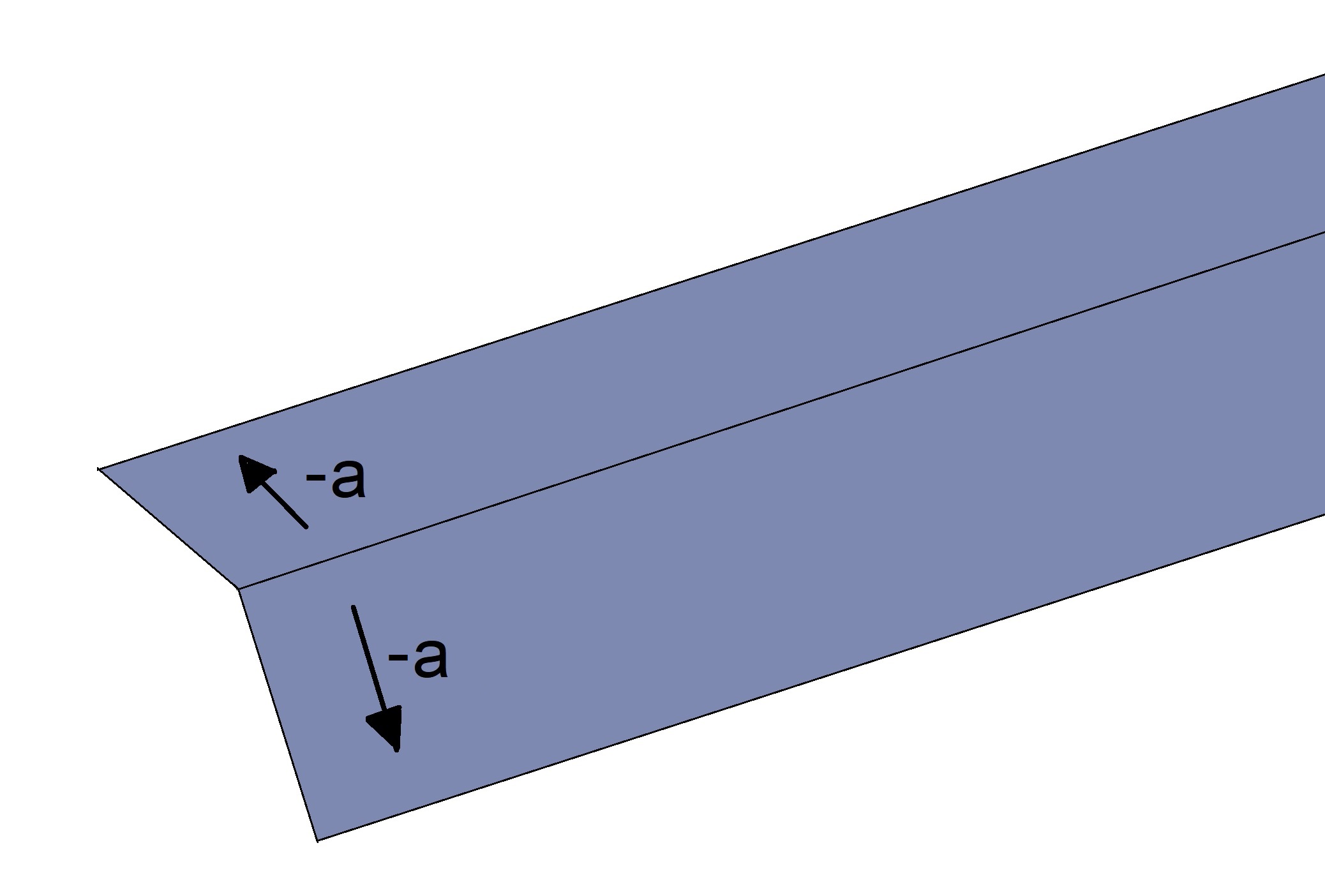
Para esse abaulamento (a) são recomendados alguns valores, que dependem do tipo de revestimento da estrada. São eles:
- Revestimentos betuminosos com granulometria aberta: 2,5 % a 3,0 %;
- Revestimentos betuminosos de alta qualidade (CBUQ): 2,0 %
- Pavimento de concreto de cimento: 1,5 %.
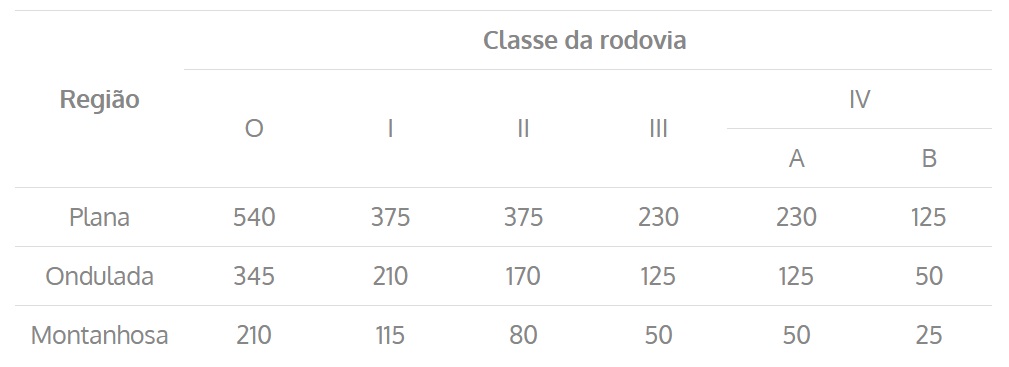
Resumidamente, os valores de raio mínimo para que seja necessário superelevação são expressos na tabela abaixo:
Tabela 1 – Raios que dispensam superelevação
Cálculo da superelevação
Supondo que o raio da curva que você deseja projetar seja inferior ao valor da tabela 1, necessitaremos, neste caso, aprender a calcular a sua superelevação.
Para tanto, faremos uma pequena demonstração de como é calculada a superelevação a partir das forças atuantes sobre o veículo em curva.
Para isso, considere a situação da figura abaixo.
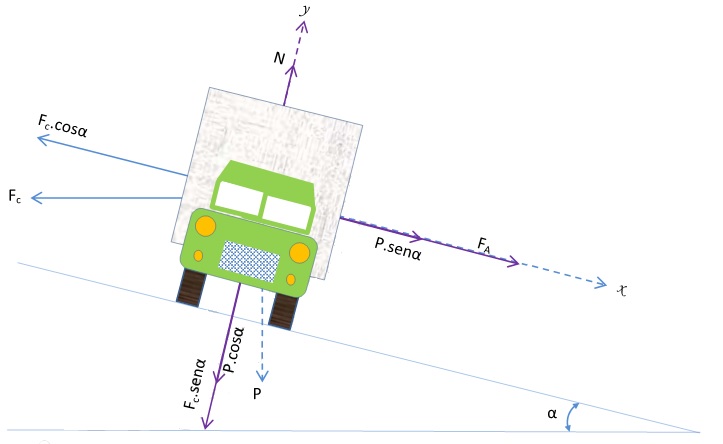
A superelevação nada mais do que a tangente da inclinação da pista, conforme abaixo:
\mathrm{e=100.tg(α)}
No entanto, o mais provável é que essa inclinação α não seja conhecida. Nesse caso, a superelevação também pode ser calculada a partir da velocidade diretriz e do raio da curva.
Através da imagem acima podemos constatar que:
\mathrm{F_c.cos(α)=P.sen(α)+F_a}
Desenvolvendo a formulação acima, podemos chegar à equação a seguir:
\mathrm{e=100\cdot\left(\dfrac{V^2}{127.R}-f\right)}
Onde:
- e é a superelevação (%);
- V é velocidade diretriz (km/h);
- R é raio de curvatura (m);
- f é o coeficiente de atrito transversal entre pneu e o pavimento, tabela 2.
Tabela 2 – Valores máximos admissíveis para os coeficientes de atrito transversal f
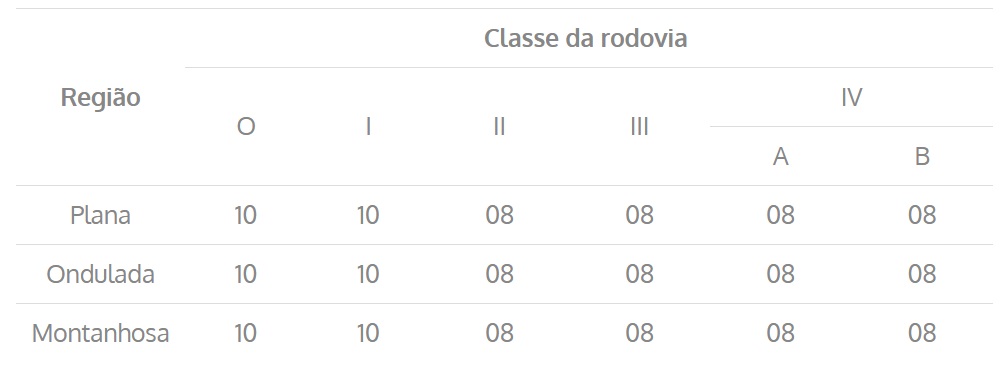
Vale ressaltar que os valores máximos admissíveis de f apresentados na tabela acima só são utilizados para condições limites, ou seja, para curvas horizontais de raios mínimos (tabela 3) e com as superelevações máximas (tabela 4).
Tabela 3 – Raio mínimo (m) para uma superelevação máxima
Superelevação mínima
A superelevação mínima para uma curva equivale (em módulo) ao valor do abaulamento nos trecho retilíneos da estrada.
Superelevação máxima
Já a superelevação máxima é calculada de acordo com a formulação a baixo:
\mathrm{e_{máx}=100\cdot\left(\dfrac{V^2}{127.R_{mín}}-f_{máx}\right)}
Onde:
- emáx é a superelevação máxima (%);
- V é velocidade diretriz (km/h);
- Rmín é raio de curvatura mínimo (m), tabela 3;
- fmáx é o coeficiente de atrito transversal máximo, tabela 2.
Para facilitar, a superelevação máxima também pode ser obtida através da tabela abaixo, dependendo das características da região e da classe da rodovia.
Tabela 4 – Superelevação máxima (%)
Superelevação recomendada
Por sua vez, a superelevação recomendada, ou seja, a que de fato será utilizada no projeto, se dá em função da máxima e do raio da curva, conforme a expressão abaixo:
\mathrm{e_R=e_{máx}\cdot\left(\dfrac{2.R_{mín}}{R}-\dfrac{R_{mín}^2}{R^2}\right)}
Onde:
- eR é a superelevação recomendada (%);
- emáx é a superelevação máxima (%), tabela 4;
- R é raio de curvatura (m);
- Rmín é raio de curvatura mínimo (m), tabela 3.
Distribuição da superelevação da curva
Agora que já aprendemos como calcular a superelevação recomendada para o seu projeto, o próximo passo é saber como distribuí-la ao longo da curva horizontal, seja ela simples ou com transição.
Curva horizontal simples
Para começarmos a distribuição da superelevação na curva simples, precisamos separá-la em alguns trechos.
Para isso, iremos arbitrar P como sendo a estaca de início da superelevação da curva horizontal simples e P’, a estaca de fim. Arbitraremos também os pontos A e B como sendo as estaca de início e fim da superelevação máxima recomendada, respectivamente.
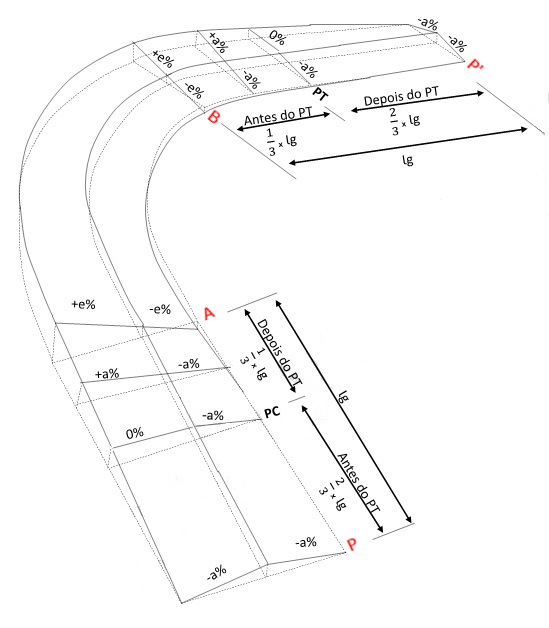
Primeiro trecho: Estaca P a PC (tangente)
O primeiro trecho começa na estaca P e vai até a estaca PC, ou seja, até o início da curva simples e mede o equivalente a \mathrm{\dfrac{2.lg}{3}}, sendo lg o comprimento do trecho do giro da plataforma e pode ser calculado por:
\mathrm{lg=\left(\dfrac{a}{g}+\dfrac{e}{2.g}\right)\cdot{L}}
Onde:
- lg é o comprimento do trecho do giro da plataforma (m);
- a é o abaulamento do trecho em tangente (%);
- eR é a superelevação máxima recomendada (%);
- g é a declividade longitudinal da borda externa (%), tabela 5;
- L é a largura da pista de rolamento (m).
Tabela 5 – Declividade longitudinal da borda da pista no trecho do giro
Desse modo, a estaca P que arbitramos pode ser encontrada através da equação:
\mathrm{P=PC-\dfrac{2.lg}{3}}
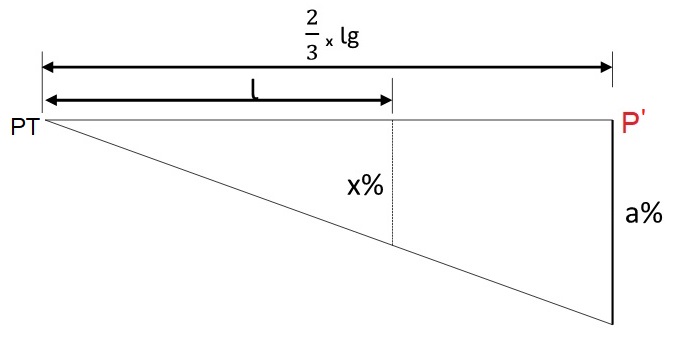
Encontrados as estacas de início e fim do primeiro trecho, podemos distribuir a superelevação, lembrando a inclinação das faixas da estrada se comportam da seguinte forma:
a) Na faixa de rolamento interna da curva, a superelevação se mantém igual ao abaulamento em tangente (a)
b) Na faixa de rolamento externa da curva, a superelevação vai de a (abaulamento em tangente) até zero ao longo do comprimento, de acordo com a equação abaixo:
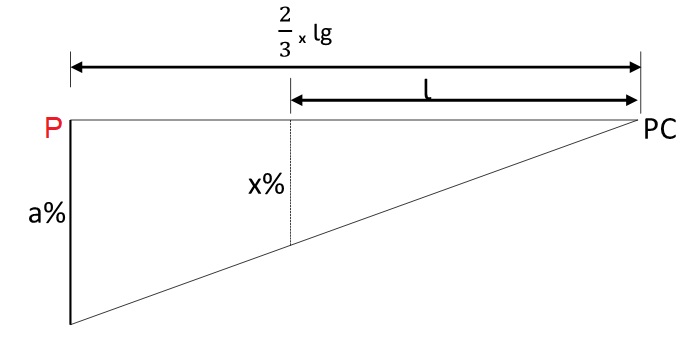
\mathrm{x=\dfrac{a}{(2/3).lg}\cdot{l}}
Onde:
- x é a superelevação em qualquer ponto do trecho (%);
- a é o abaulamento em tangente (%);
- lg é o comprimento do trecho do giro da plataforma (m);
- l é a distância de um ponto em relação ao PC (m).
Segundo trecho: Estaca PC a A (borda da curva)
O segundo trecho começa na estaca PC e vai até a estaca A e mede o equivalente a \mathrm{\dfrac{lg}{3}}.
Desse modo, a estaca A que arbitramos pode ser encontrada através da equação:
\mathrm{A=PC+\dfrac{lg}{3}}
Encontrados as estacas de início e fim do segundo trecho, podemos distribuir a superelevação, lembrando a inclinação das faixas da estrada se comportam da seguinte forma:
a) Na faixa de rolamento interna da curva, a superelevação se mantém igual ao abaulamento em tangente (a) até que o valor absoluto da declividade da faixa externa ultrapasse o da interna e, então, as declividades transversais das faixas terão a mesma valor absoluto e sinais contrários
b) Na faixa de rolamento externa da curva, a superelevação vai de zero até eR (superelevação máxima recomendada) ao longo do comprimento, de acordo com a equação abaixo:
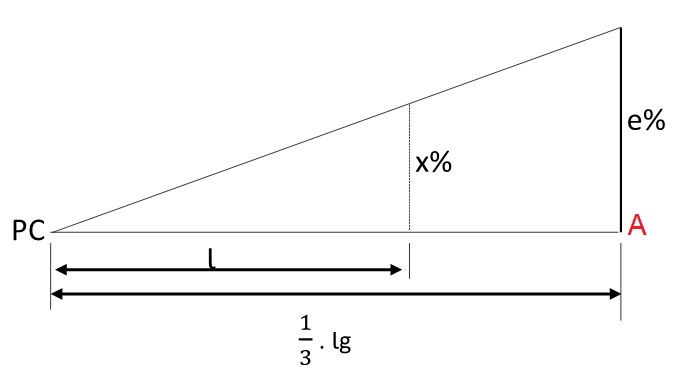
\mathrm{x=\dfrac{e}{(1/3).lg}\cdot{l}}
Onde:
- x é a superelevação em qualquer ponto do trecho (%);
- eR é a superelevação máxima recomendada (%);
- lg é o comprimento do trecho do giro da plataforma (m);
- l é a distância de um ponto em relação ao PC (m).
Terceiro trecho A a B (meio do curva)
No meio da curva circular, ou seja, entre as estacas A e B, a declividade da pista é constante.
Como já conhecemos a estaca de início do trecho (A), basta agora calcularmos a estaca final, que se dá pela equação abaixo:
\mathrm{B=TC-\dfrac{2.lg}{3}}
Agora, vejamos como se comporta a inclinação das faixas no meio da curva simples:
a) Na faixa de rolamento interna da curva, a declividade equivale à superelevação máxima (-e);
b) Na faixa de rolamento externa da curva, a declividade equivale à superelevação máxima (+e).

Quarto trecho: estaca B a PT (borda da curva)
Para o quarto trecho a situação é similar ao segundo trecho, só que de maneira inversa.
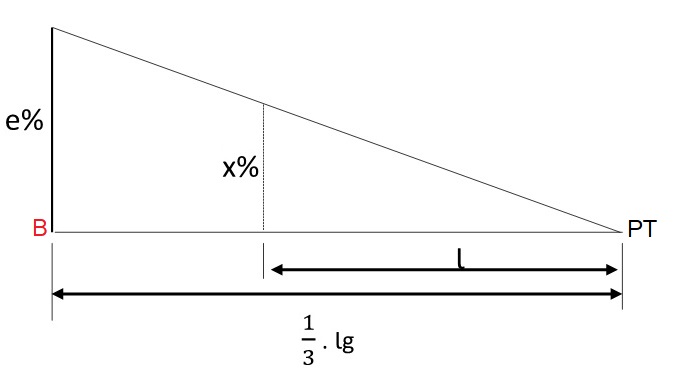
Quinto trecho: estaca PT a P’ (tangente)
Por fim, para o trecho final da distribuição, a situação é similar ao primeiro trecho, mas de maneira inversa.
Curva horizontal com transição
Para começarmos a distribuição da superelevação na curva com transição, precisamos também separá-la em alguns trechos.
Para isso, assim como na curva simples, iremos arbitrar P como sendo a estaca de início da superelevação da curva horizontal com transição e P’, a estaca de fim.
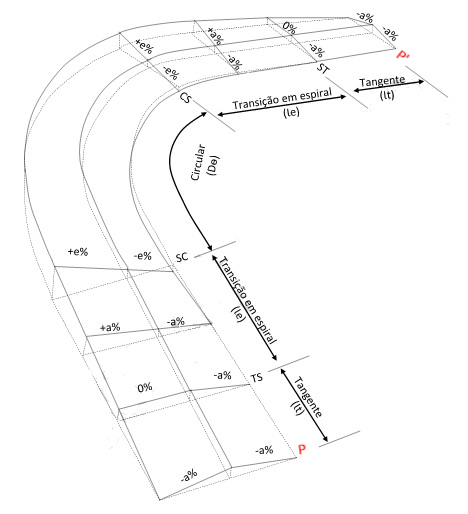
Primeiro trecho: estaca P a TS (tangente)
Chamaremos de P a estaca onde a superelevação se inicia e é calculada por:
\mathrm{P=TS-lt}
Para isso precisamos encontrar o valor de lt, que é o trecho reto em que a inclinação transversal no lado externo da curva varia de a até zero e no lado interno se mantém, e é calculado por:
\mathrm{lt=\dfrac{L.a}{g}}
Onde:
- lt é o comprimento em tangente (m);
- L é a largura da faixa de rolamento (m);
- a é o abaulamento em tangente (%);
- g é a declividade longitudinal da borda externa (%), tabela 5.
Encontrados as estacas de início e fim do primeiro trecho, podemos distribuir a superelevação, lembrando a inclinação das faixas da estrada se comportam da seguinte forma:
a) Na faixa de rolamento interna da curva, a superelevação se mantém igual ao abaulamento em tangente (a)
b) Na faixa de rolamento externa da curva, a superelevação vai de a (abaulamento em tangente) até zero ao longo do comprimento, de acordo com a equação abaixo:
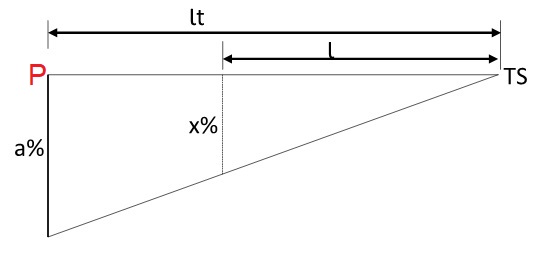
\mathrm{x=\dfrac{a}{lt}\cdot{l}}
Onde:
- x é a superelevação em qualquer ponto do trecho (%);
- a é o abaulamento em tangente (%);
- lt é o comprimento em tangente (m);
- l é a distância de um ponto em relação ao TS (m).
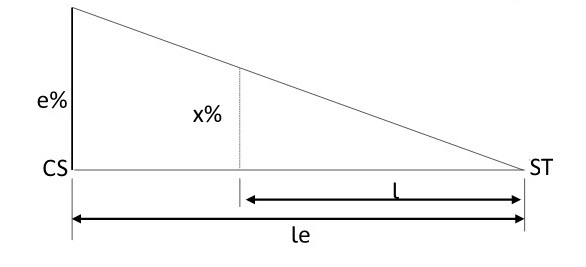
Segundo trecho: estaca TS a SC (espiral)
O segundo trecho da distribuição é o primeiro ramo da espiral de transição, que vai da estaca TS a SC e mede le.
Dessa forma, a distribuição da superelevação obedece ao seguinte critério:
a) Na faixa de rolamento interna da curva, a superelevação se mantém igual ao abaulamento em tangente (a) até que o valor absoluto da inclinação da faixa externa a ultrapasse e, então, a inclinação das duas faixas seguirão iguais em valor e com sinais opostos.
b) Na faixa de rolamento externa da curva, a superelevação vai de zero a eR (superelevação máxima recomendada) ao longo do comprimento, de acordo com a equação abaixo:
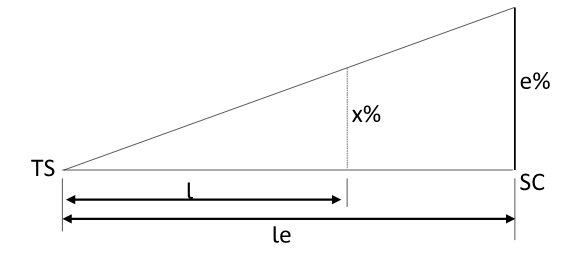
\mathrm{x=\dfrac{e}{le}\cdot{l}}
Onde:
- x é a superelevação em qualquer ponto do trecho (%);
- eR é a superelevação máxima recomendada (%);
- le é o comprimento do trecho em espiral (m);
- l é a distância de um ponto em relação ao TS (m).
Terceiro trecho: estaca CS a CS (curva circular)
Para esse trecho não é necessário calcular a inclinação, pois ela se mantém constante e igual à superelevação máxima recomendada (eR), para as duas faixas.
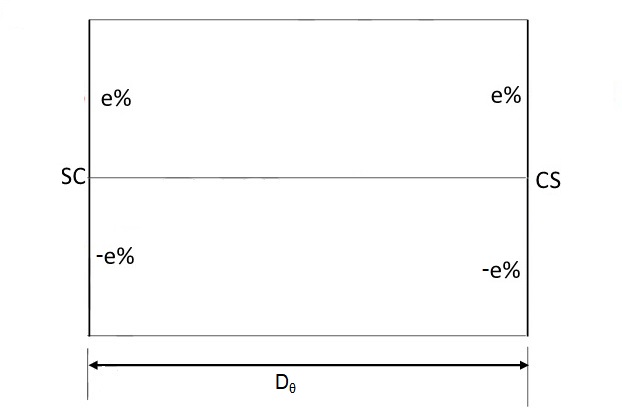
Quarto trecho: estaca CS a ST (espiral)
Para esse trecho, o raciocínio é semelhante ao segundo trecho, mas de maneira inversa.
Isso quer dizer que a superelevação externa em cada uma das estacas desse trecho diminui até chegar a zero, enquanto a inclinação interna seguirá igual à externa, em módulo, até chegar ao valor do abaulamento e, então, se manterá.
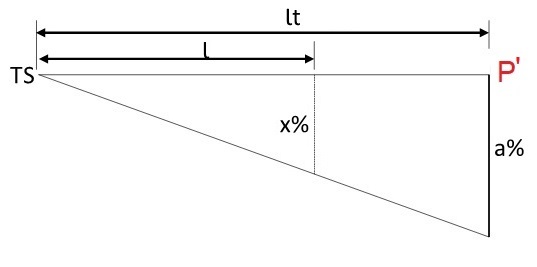
Quinto trecho: estaca ST a P’ (tangente)
Por fim, esse trecho também é semelhante ao primeiro trecho, mas de maneira inversa.
Isso quer dizer que a superelevação externa em cada uma das estacas desse trecho diminui até chegar a ao valor do abaulamento em tangente (a), enquanto o abaulamento interno seguirá constante em todo o trecho.
Pois bem pessoal, essas foram algumas considerações a respeito da superelevação para curvas horizontais e se você quiser exercitar tudo o que a prendeu nesse post, é só clicar aqui.
Ou, se preferir, confira o super e-Book GRATUITO sobre Projeto Rodoviário que preparamos pra você.
[ebook-projetos-rodoviarios]É claro, no entanto, que esse universo é muito mais amplo do que conseguimos abordar em um e-Book.
Então, se você quiser se aprofundar mais nessa área, sugiro que conheça o curso online Formação em Estradas de um dos nosso parceiros, o Grupo HCT, que é um centro de aperfeiçoamento profissional atuante na área tecnológica desde 1997.
Dito isso, ficamos por aqui e se gostou, não deixa de seguir a gente no Instagram e também no Youtube para receber todas as novidades.
Fonte:
ALBUQUERQUE, Marcos. Superelevação. Teresina: UFPI, 2017.
MACEDO, Edivaldo Lins. Noções de Topografia Para Projetos Rodoviarios. 2008. Disponível em: <http://www.topografiageral.com/>. Acesso em: 12 set 2019.

Engenheira Civil pela Universidade Federal do Piauí, engenheira de obra, perita judicial e pós-graduanda em Avaliação, Auditoria e Perícias de Engenharia.