Todo mundo gosta de uma estrada retinha, não é mesmo? Você consegue viajar bem mais rápido, gasta menos combustível, economiza, além de que consegue percorrer uma distância menor.
Seria ótimo se todas as estradas fossem perfeitamente retas e planas, mas a realidade é bem diferente. Isso porque há varias limitações para isso, sejam os obstáculos da natureza, sejam as obras existentes no meio do percurso ou, até mesmo, as limitações de custo de regularização do terreno.
É aí que as curvas entram para facilitar a construção das estradas e garantir a sua continuidade quando, por exemplo, há obstáculos intransponíveis ao seu traçado ou, até mesmo, para evitar custos excessivos durante a sua execução.
É por isso mesmo que, nesse post, estudaremos as curvas horizontais do tipo simples e ainda aprenderemos como realizar o estaqueamento de um trecho curvo de um projeto rodoviário.
Mas antes de começarmos nossa aventura aqui, recomendamos que dê uma rápida olhada no nosso post sobre projetos rodoviário e seus elementos, clicando aqui.
Ah, e antes que eu esqueça, temos videoaula sobre curva simples também, se quiser assistir é só dar play.
Agora vamos lá?
Curva horizontal simples
Dizemos que uma curva é simples quando o seu raio é constante, ou seja, quando se utiliza apenas uma curva circular para realizar a transição entre os trecho retilíneos de estrada.
Além do mais, é um tipo de curva muito empregado em razão da sua simplicidade para projeto e locação, como veremos nesse post.
Elementos
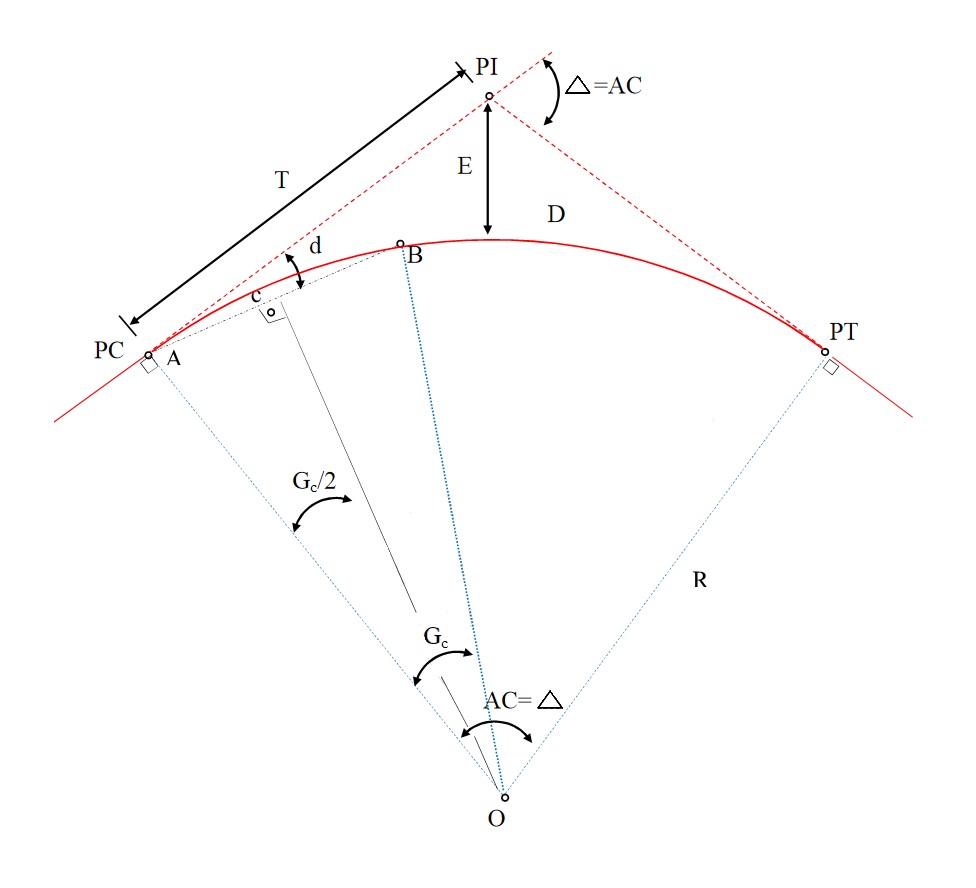
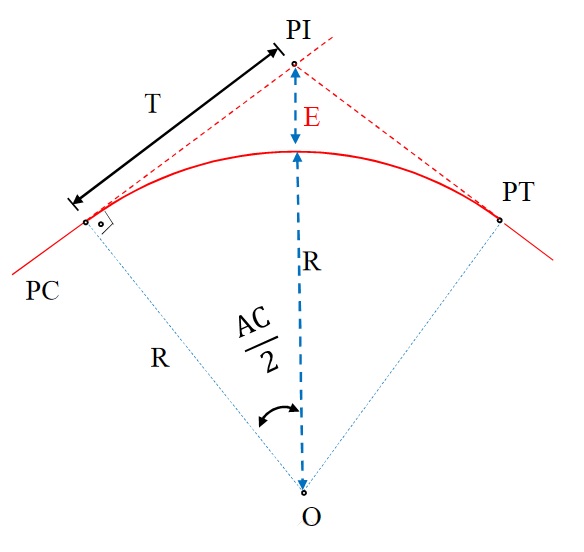
Para começarmos a entender o projeto de curvatura de uma estrada, iremos agora conhecer os elementos componentes da curva horizontal simples.
Onde:
- PC é o ponto de curvatura;
- T é a tangente externa;
- PI é o ponto de interseção das tangentes;
- Δ é o ângulo de deflexão;
- AC é o ângulo central da curva;
- E é o afastamento da curva;
- c é a corda;
- d é a deflexão sobre as tangentes;
- D é o desenvolvimento da curva;
- PT é o ponto de tangência;
- Gc é o grau da curva;
- AC é o ângulo central da curva;
- R é o raio da curva circular;
- O é o centro da curva.
Agora que já fomos apresentados aos elementos da curva simples, iremos agora estudá-los individualmente.
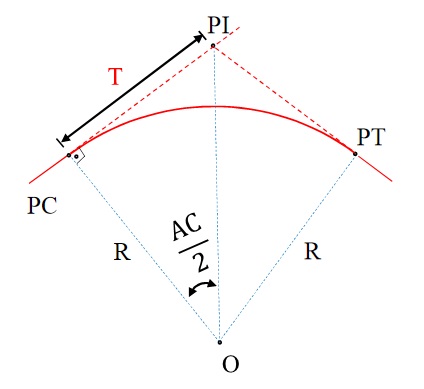
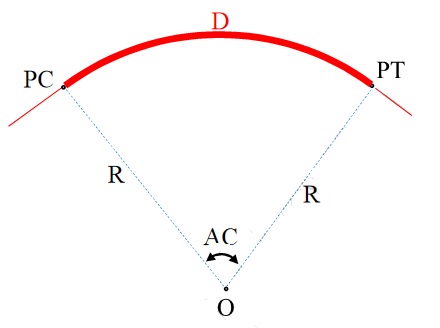
Ângulo central da curva
O ângulo central (AC) nada mais é do que o ângulo formado entre os pontos PC e PT da curva.
Ângulo de deflexão
O ângulo de deflexão (Δ) é o desvio no sentido horário entre as duas tangentes externas e é, numericamente, igual ao ângulo central (AC).
Raio da curva circular
O que é um raio de uma curva (R) nós já sabemos. Neste caso, o que precisamos saber sobre ele é que, para uma obra rodoviária, o raio da curva é selecionado de acordo com as características técnicas da estrada e da topografia da região.
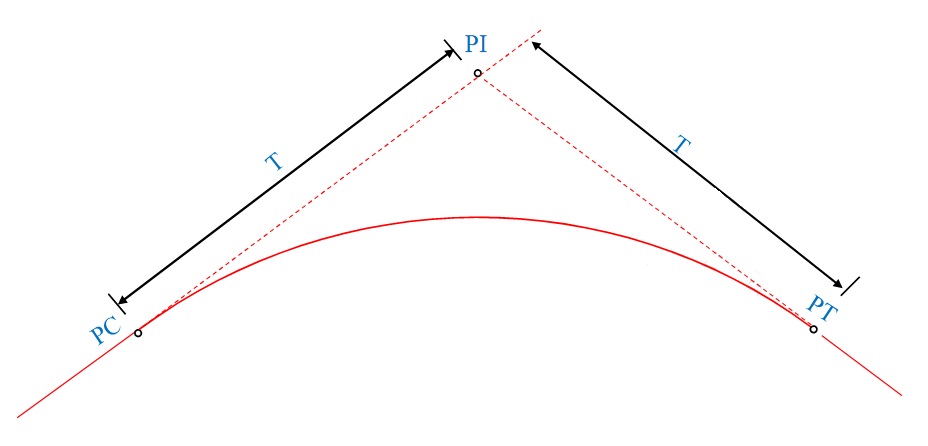
Ponto de interseção das tangentes
Como o próprio nome já diz, o ponto de interseção (PI) nada mais é do que o único ponto de cruzamento entre as as tangentes que tocam os pontos PC e PT.
Ponto de curvatura
O ponto de curvatura (PC), por sua vez, é o ponto de início da curva, ou seja, é exatamente onde o trecho retilíneo da estrada termina e é calculado pela expressão abaixo.
\mathrm{PC=PI-T}
Onde:
- PC é o ponto de curvatura (m);
- PI é o ponto de interseção das tangentes (m);
- T é a tangente externa (m);
Ponto de tangência
Já o ponto de tangência (PT) é o ponto final da curva, ou seja, é onde o trecho retilíneo volta a se iniciar e é calculado pela expressão abaixo.
\mathrm{PT=PC+D}
Onde:
- PT é o ponto de tangência (m);
- PC é o ponto de curvatura (m);
- D é o desenvolvimento da curva (m).
Tangente externa
Tangente externa (T), neste caso, representa os segmentos de reta que vão do PC ao PI ou do PI ao PT. T é, então, calculado por:
\mathrm{T=R.tg\left(\dfrac{AC}{2}\right)}
Onde:
- T é a tangente externa (m);
- R é o raio da curva circular (m);
- AC é o ângulo central da curva (graus).
Desenvolvimento da curva
Desenvolvimento da curva (D), neste caso, representa o comprimento do arco que vai desde o PC ao PT e é obtido pela seguinte expressão:
\mathrm{D=\dfrac{R.AC.π}{180º}}
Onde:
- D é o desenvolvimento da curva (m);
- AC é o ângulo central da curva (graus);
- R é o raio da curva circular (m);
- π é uma constante ≅ 3,1416.
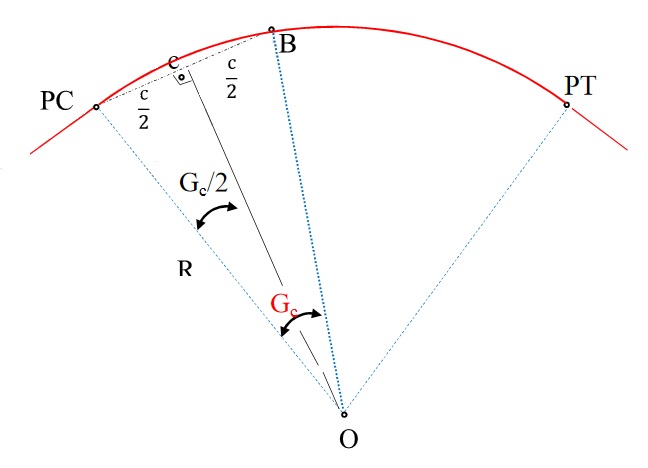
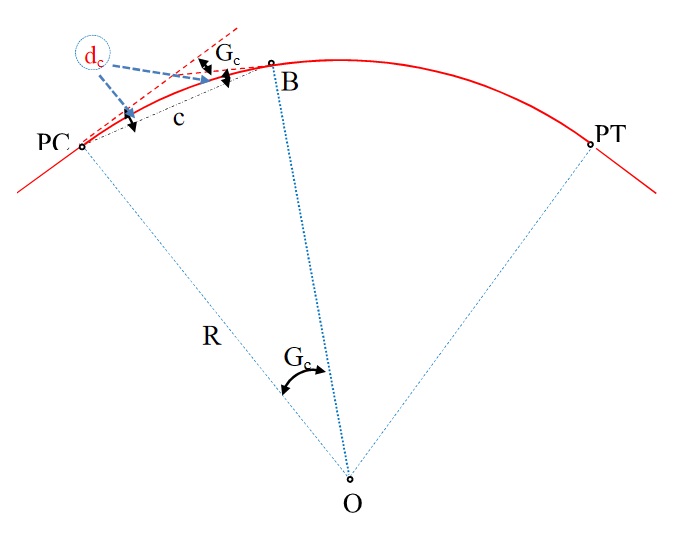
Grau da curva
Grau da curva (Gc) refere-se ao ângulo central que compreende uma corda de um dado comprimento e é calculado por:
\mathrm{Gc=2.arcsen\left(\dfrac{c}{2.R}\right)}
Onde:
- Gc é o grau da curva (rad);
- c é a corda (m);
- R é o raio da curva circular (m).
Corda
A corda da curva (c) nada mais é que o segmento de reta que liga duas estacas pertencentes à curva e seu comprimento é selecionado de acordo com o seguinte critério.
Tabela 1 – Comprimento da corda em função do raio
| Raio (m) | Corda máxima (m) |
| R<150 | 5 |
| 150≤R<300 | 10 |
| R≥300 | 20 |
Deflexão sobre as tangentes
A deflexão sobre as tangentes (d) é o ângulo formado entre a linha que liga PC a um ponto e a tangente que passa por PC e é calculada por:
\mathrm{d=\dfrac{Gc}{2}}
Onde:
- d é a deflexão sobre as tangentes (rad);
- Gc é o grau da curva (rad).
Deflexão por metro
A deflexão por metro (dm) é apenas a deflexão por unidade de comprimento e é extremamente importante para o estaqueamento da curva, pois é possível determinar a deflexão de qualquer ponto no interior da curva apenas multiplicando sua distância (em relaçaõ a PC) por dm.
\mathrm{d_m=\dfrac{d}{c}}
Onde:
- dm é a deflexão sobre as tangentes por metro (rad/m);
- d é a deflexão sobre as tangentes (rad);
- c é a corda (m).
E é o afastamento da curva
O afastamento da curva (E) é simplesmente a menor distância entre o PI e a curva e pode ser calculado de duas formas:
\mathrm{E=R\left[\dfrac{1}{cos(AC/2)}-1\right]=T.tg\left(\dfrac{AC}{4}\right)}
Onde:
- E é o afastamento da curva (m);
- R é o raio da curva circular (m);
- AC é o ângulo central da curva (rad);
- T é a tangente externa (m).
Locação da curva horizontal simples
Agora que já entendemos todos os elementos da curva simples, já podemos aprender os procedimentos básicos para a locação da curva horizontal de uma estrada. Para isso, observe os passos que serão apresentados no exemplo a seguir.
Exemplo prático
Você é responsável por um projeto rodoviário e necessita determinar os elementos de uma curva de concordância horizontal simples, sabendo que o estaqueamento da estrada é feito a cada 20 m, o ponto de interseção está localizado na estaca 100+7,40 m, o ângulo central é 30° 20’ 00” e o seu raio de curvatura mede 295 m.
RESOLUÇÃO:
Passo 01: Determinar o comprimento da corda da curva
De acordo com a tabela 1, a corda máxima para um raio de 295 m é 10 m, logo:
\mathrm{c=10\:m}
Passo 02: Calcular a tangente externa
Para o cálculo da tangente externa faremos uso apenas do raio e do ângulo central pela fórmula abaixo:
\mathrm{T=R.tg\left(\dfrac{AC}{2}\right)}
\mathrm{T=295.tg\left(\dfrac{30°\:20’\:00”}{2}\right)=79,96\:m}
Passo 03: Calcular o desenvolvimento da curva
Para o cálculo do desenvolvimento da curva também faremos uso apenas do raio e do ângulo central pela fórmula abaixo:
\mathrm{D=\dfrac{R.AC.π}{180º}}
\mathrm{D=\dfrac{295.(30°\:20’\:00”).π}{180º}=156,18\:m}
Passo 04: Calcular o afastamento da curva
Para o cálculo do afastamento da curva faremos uso apenas do ângulo central e da tangente, calculada no passo 02, pela fórmula abaixo:
\mathrm{E=T.tg\left(\dfrac{AC}{4}\right)}
\mathrm{E=79,96.tg\left(\dfrac{30°\:20’\:00”}{4}\right)=10,64\:m}
Passo 05: Calcular o grau da curva
Para o cálculo do grau da curva faremos uso apenas do raio e da corda, determinada no passo 01, pela fórmula abaixo:
\mathrm{Gc=2.arcsen\left(\dfrac{c}{2.R}\right)}
\mathrm{G10=2.arcsen\left(\dfrac{10}{2.295}\right)=1º\:56'\:32,4"}
Passo 06: Calcular a deflexão por metro
Devemos calcular a deflexão por metro, e não somente a deflexão, para que possamos encontrar a estaca de um ponto, qualquer que seja sua distância em relação ao ponto de curvatura.
\mathrm{d_m=\dfrac{d}{c}}
\mathrm{d_m=\dfrac{Gc}{2.c}}
\mathrm{d_m=\dfrac{1º\:56'\:32,4"}{2.10}=0º\:05'\:49,6"/m}
Passo 07: Locar a estaca PC
Para essa etapa, é importante lembrarmos que a distância entre duas estacas inteiras pertencentes à estrada é 20 m.
No entanto, de acordo com a corda que determinamos no passo 01, no interior da curva o estaqueamento deverá ser feito a cada 10 m, ou seja, deverá haver sempre uma estaca intermediária entre duas estacas inteiras.
Então, para realizarmos o estaqueamento da curva, começaremos pelo ponto inicial, o PC.
\mathrm{PC=PI-T}
\mathrm{PC=100+7,40\:m-79,96\:m=100-72,56\:m}
\mathrm{PC=96+80\:m-72,56\:m=96+7,44\:m}
Passo 08: Locar a estaca PT
\mathrm{PT=PC+D}
\mathrm{PT=96+7,44\:m+156,18\:m=96+163,62\:m}
\mathrm{PT=96+8+3,62\:m=104+3,62\:m}
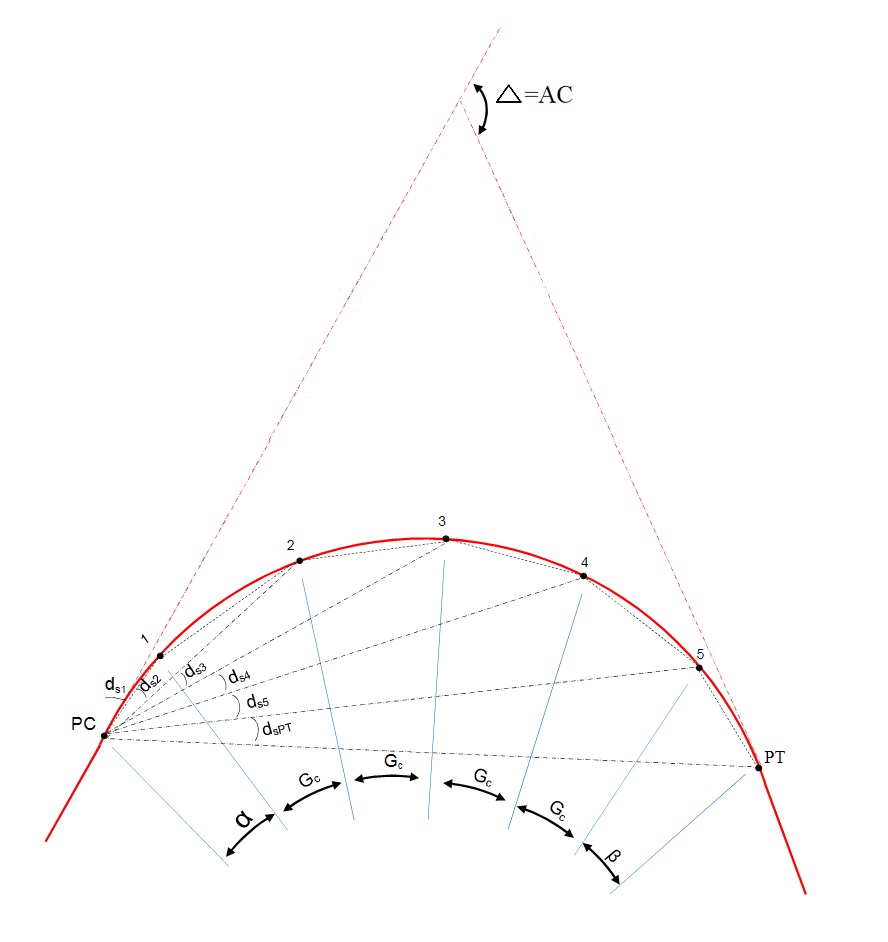
Passo 09: Calcular as deflexões parciais
Para esse passo, precisamos encontrar a deflexão parcial para 3 cordas importantes: a corda de 10 m entre as estacas intermediárias da curva, a corda de 2,56 m (10-7,44) entre PC e a primeira estaca e a corda de 3,62 m entre a última estaca e PT.
- Deflexão parcial para a corda de 10m
\mathrm{d=d_m.c}
\mathrm{d_{10}=(0º\:05'\:49,6"/m).10=0º\:58'\:16"}
- Deflexão parcial para a corda de 2,56m
\mathrm{d=d_m.c}
\mathrm{d_{2,56}=(0º\:05'\:49,6"/m).2,56=0º\:14'\:55"}
- Deflexão parcial para a corda final de 3,62m
\mathrm{d_{3,62}=(0º\:05'\:49,6"/m).3,62=0º\:21'\:5,55"}
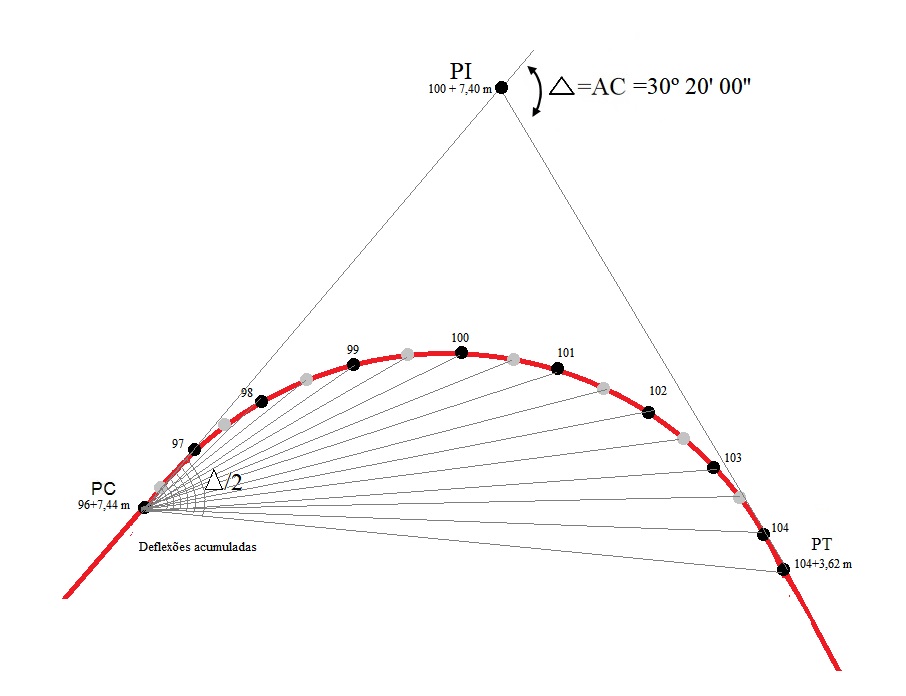
Após o cálculo da deflexão parcial, seguiremos para o preenchimento da caderneta de anotação e locação das demasi estacas, conforme abaixo.
Passo 10: Locar as demais estacas
Neste caso, faremos o estaqueamento da estrada com base na soma das deflexões parciais em relação ao ponto PC, ou seja, as deflexões serão acumuladas.
Isso que dizer que a deflexão da estaca 2 será a deflexão parcial da estaca 1 (em relação a PC) mais a deflexão entre as estacas 1 e 2 e assim sucessivamente.
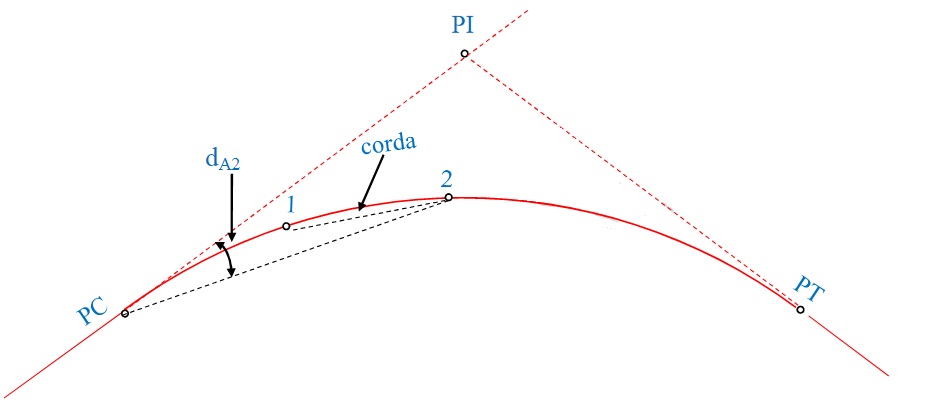
Tabela 2 – Caderneta de Locação
| Estaca | Deflexão | ||
| Inteira | Fracionária | Parcial | Acumulada |
| PC – 96 | 7,44 m | 00º 00′ 00″ | 00º 00′ 00″ |
| 96 | 10,00 m | 00º 14′ 55″ | 00º 14′ 55″ |
| 97 | 00º 58′ 16″ | 01º 13′ 11″ | |
| 97 | 10,00 m | 00º 58′ 16″ | 02º 11′ 27″ |
| 98 | 00º 58′ 16″ | 03º 09′ 43″ | |
| 98 | 10,00 m | 00º 58′ 16″ | 04º 07′ 59″ |
| 99 | 00º 58′ 16″ | 05º 06′ 15″ | |
| 99 | 10,00 m | 00º 58′ 16″ | 06º 04′ 31″ |
| 100 | 00º 58′ 16″ | 07º 02′ 47″ | |
| 100 | 10,00 m | 00º 58′ 16″ | 08º 01′ 03″ |
| 101 | 00º 58′ 16″ | 08º 59′ 19″ | |
| 101 | 10,00 m | 00º 58′ 16″ | 09º 57′ 35″ |
| 102 | 00º 58′ 16″ | 10º 55′ 51″ | |
| 102 | 10,00 m | 00º 58′ 16″ | 11º 54′ 07″ |
| 103 | 00º 58′ 16″ | 12º 52′ 23″ | |
| 103 | 10,00 m | 00º 58′ 16″ | 13º 50′ 39″ |
| 104 | 00º 58′ 16″ | 14º 48′ 55″ | |
| PT – 104 | 3,62 m | 00º 21′ 5,55″ | 15º 10′ 0,55″ |
Lembrando que a deflexão acumulada entre PC no PT equivale à metade do ângulo de deflexão (Δ), que é igual ao ângulo central (AC). No nosso resultado houve apenas uma pequena diferença de 1,1″ em virtude das aproximações.
Desse modo, o resultado final do nosso estaqueamento é o seguinte:
Pois bem pessoal, essas foram algumas considerações a respeito das curvas horizontais simples, espero muito que esse post tenha sido útil pra você e se quiser saber também sobre as curvas compostas, é só clicar aqui.
Ah, e não deixe de acompanhar o e-Book gratuito sobre Projeto Rodoviário que nós preparamos pra você!!!
[ebook-projetos-rodoviarios]É claro, no entanto, que esse universo é muito mais amplo do que conseguimos abordar em um e-Book.
Então, se você quiser se especializar nessa área, sugiro que conheça o curso online Formação em Estradas de um dos nosso parceiros, o Grupo HCT, que é um centro de aperfeiçoamento profissional atuante na área tecnológica desde 1997.
Dito isso, ficamos por aqui e se gostou, não deixa de seguir a gente no Instagram e também no Youtube para receber todas as novidades.
Fonte:
ALBUQUERQUE, Marcos. Curva Horizontal Simples. Teresina: UFPI, 2017.

Engenheira Civil pela Universidade Federal do Piauí, engenheira de obra, perita judicial e pós-graduanda em Avaliação, Auditoria e Perícias de Engenharia.