Se você segue nosso blog, sabe que já tratamos sobre diversas formas de determinação da tensão admissível do solo. Abordamos o ensaio de placa, o método teórico de Terzaghi e alguns métodos semi-empíricos bastante utilizados nacionalmente.
Também já fizemos a aplicação prática do método teórico e semi-empírico através da resolução de um problema prático!
Porém, você pode se perguntar: quando há presença de solos estratificados, caso eu tenha uma camada de solo menos resistente abaixo da cota de assentamento da minha fundação? Como devo considerar a influência dessa camada no cálculo da tensão admissível?
Calma, não se desespere! Nesse post responderemos suas dúvidas de maneira sucinta e prática! Vamos lá?
Solos estratificados e bulbo de tensões
Antes de tratarmos especificamente sobre o cálculo da tensão admissível para solos estratificados, julgo importante falarmos um pouco sobre o bulbo de tensões.
Caso você se interesse pelo tema, temos um post completo com vídeo no nosso blog. Aqui faremos um pequeno resumo para que você entenda a importância dele nesse tema.
Então, bulbo de tensões é o conjunto de várias curvas de isovalores de tensões verticais no solo induzidas por um carregamento externo.
Esse conceito pode parecer difícil e confuso, mas sua aplicação é relativamente simples!
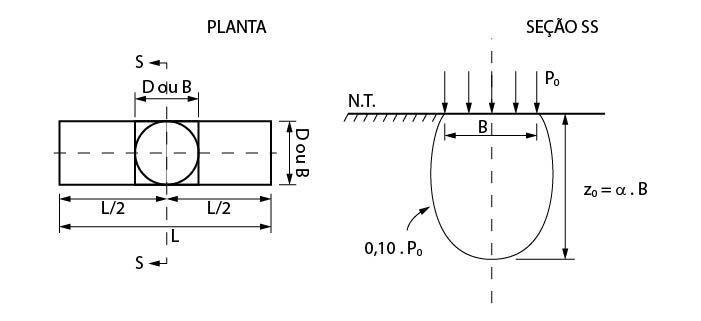
O bulbo de tensões nos dá até que profundidade uma carga externa influencia consideravelmente as tensões no solo. Essa profundidade varia basicamente de acordo com o formato da fundação, como mostrado na tabela abaixo.
| Forma da fundação | \mathrm{\alpha} | |
| Circular ou quadrada | 2,0 | |
| Retangular
(\mathrm{L\cdot B}) |
1,5 | 2,5 |
| 2,0 | 3,0 | |
| 3,0 | 3,5 | |
| 4,0 | 4,0 | |
| Infinitamente longa | 6,5 | |
Então, podemos dizer por exemplo, que para uma sapata quadrada, a tensão transmitida no solo por ela, só terá efeitos consideráveis até uma profundidade de duas vezes a largura de sua base.
Ou seja, vamos resumir: se minha sapata tem dimensões de base de 1,0 m x 1,0 m e a camada com resistência menor se encontra a mais de 2,0 metros de profundidade da cota de assentamento, podemos ignorar essa camada e calcular a tensão admissível apenas para a cota de assentamento, visto que na profundidade da camada de baixa resistência, as tensões provocadas pela sapata terão efeitos desconsideráveis, segundo a teoria do bulbo de tensões.
Entendeu? Ficou claro pra você?
Apenas para ser mais enfático, vamos apresentar abaixo uma figura. Uma com uma sapata de menor dimensão, onde o bulbo de tensões não chega até a camada de menor resistência e outra onde o bulbo chega a essa camada.
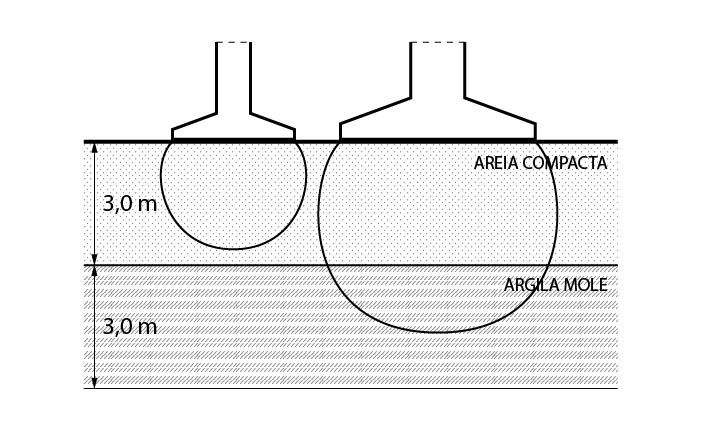
Para a sapata da esquerda nós podemos ignorar a camada de argila mole na determinação da tensão admissível do solo na cota de assentamento.
Mas para a sapata à direita, como seu bulbo de tensões chega até a camada de menor resistência, nós precisamos determinar a influência dessa camada na tensão admissível da cota de assentamento da fundação.
E aí você pergunta: como faremos isso?
Então, agora que você sabe quando deve considerar a influência de uma camada menos resistente na tensão admissível do solo, vamos partir para quantificar essa influência.
Determinação da tensão admissível
Então, para melhor entendimento do cálculo da tensão admissível para solos estratificados, vamos considerar a figura abaixo.
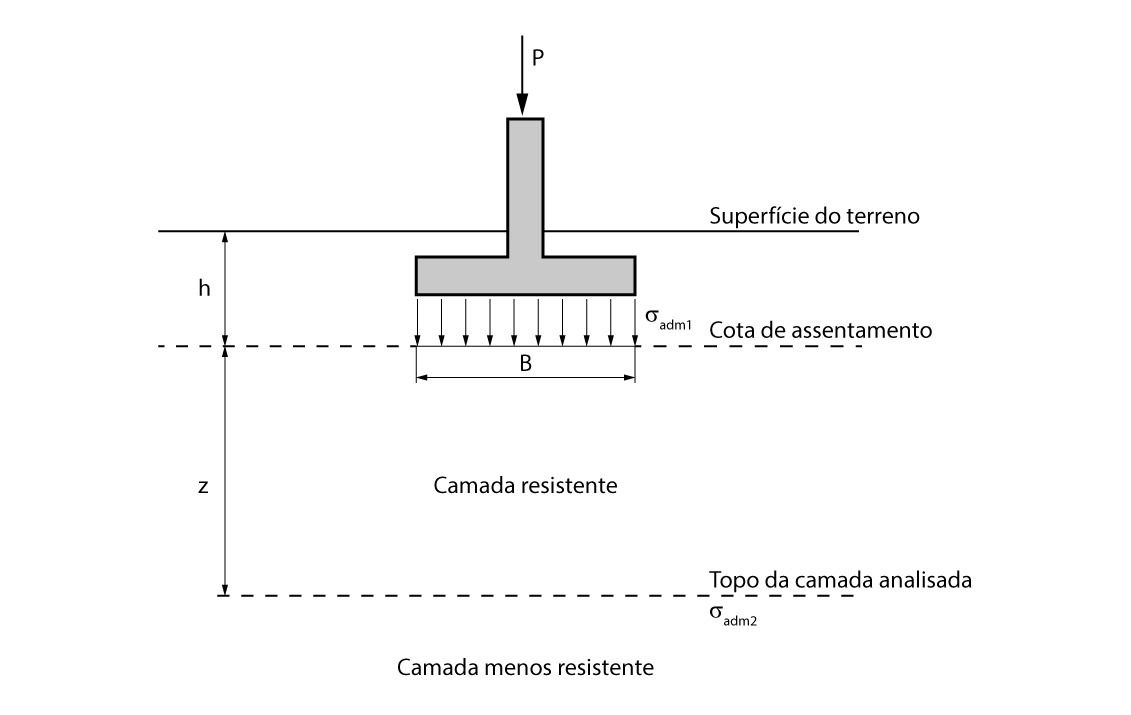
Nela, temos a apresentação das seguintes variáveis:
- \mathrm{\sigma_{adm1}}: tensão admissível na cota de assentamento da sapata;
- z: distância entre a cota de assentamento da sapata e a camada menos resistente;
- B: largura da sapata;
- \mathrm{\sigma_{adm2}}: tensão admissível no topo da camada menos resistente.
Então, o que precisamos fazer agora é relativamente simples: basta compararmos a tensão provocada pela sapata na camada menos resistente com a própria tensão admissível dessa camada!
Como assim, Filipe? Não entendi.
Calma, é simples! Como já dissemos anteriormente no conceito de bulbo, a tensão provocada na sapata vai chegar até a camada de menor resistência, mas nessa camada o valor dessa tensão será menor, por a carga vai se espraiando no solo.
Uma maneira fácil de supor esse espraiamento é pela razão 1:2, como mostrado na figura abaixo.

Temos então que, a tensão provocada pela sapata no topo da camada menos resistente, chamaremos de \mathrm{\Delta\sigma}.
E como calculamos \mathrm{\Delta\sigma}?
Perceba que a carga que atua na sapata é a mesma que irá atuar na camada mais profunda e como a carga é um produto da tensão pela sua área de atuação, temos, considerando a sapata quadrada de lado B e que a sapata foi dimensionada para a tensão admissível na sua cota de assentamento:
\mathrm{\Delta\sigma \cdot (B+L)^{2}= \sigma_{adm1} \cdot (B)^{2}}
\mathrm{\Delta\sigma = \dfrac{\sigma_{adm1} \cdot (B)^{2}}{(B+L)^{2}}}
E agora?
O que precisamos fazer nada mais é do que comparar \mathrm{\Delta\sigma} e \mathrm{\sigma_{adm2}}, chegando então a duas proposições possíveis:
- \mathrm{\Delta\sigma \leq \sigma_{adm2}}: Isso significa dizer que a tensão adicional na camada ocasionada pela sapata é menor do que a tensão admissível do solo. Nesse caso, não precisamos fazer nenhuma minoração na tensão admissível da cota de assentamento (\mathrm{\sigma_{adm1}}). Logo, para essa primeira situação:
\mathrm{\sigma_{adm1}' = \sigma_{adm1}}
Onde:
\mathrm{\sigma_{adm1}'} : tensão admissível final da cota de assentamento.- \mathrm{\Delta\sigma > \sigma_{adm2}}: Isso significa dizer que a tensão adicional na camada ocasionada pela sapata é maior do que a tensão admissível do solo. Nesse caso, ocorreria uma possível ruptura na camada menos resistente, logo precisamos minorar a tensão admissível na cota de assentamento. Teremos então que:
\mathrm{\sigma_{adm1}' = \sigma_{adm1}\cdot\dfrac{\sigma_{adm2}}{\Delta\sigma}}
Pronto! Nesse post fizemos uma pequena recordação de bulbo de tensões e a partir desses conceitos, conseguimos determinar a tensão admissível em solos estratificados!
Espero que não tenham ficado dúvidas, mas aso você ainda tenha alguma ou tenha sugestões para temas futuros, deixa nos comentários que a gente responde!
Não deixe de seguir nosso blog, assinar nossa newsletter, além de acompanhar nosso canal no Youtube e ficar por dentro das novidades!
Até a próxima!
Engenheiro Civil, Especialista em Estruturas e Fundações. Ex-goleiro, Pseudosommelier de Cervejas e Poeta Freelancer Fajuto.

Parabéns pelo post. Estou começando a seguir seu blog e canal no YouTube. Formo em Engenharia Civil no final deste ano
Muito obrigado pelo elogio, Alexandre! Qualquer dúvida ou sugestão de post que você tiver, só mandar por aqui que a gente responde!