Bulbo de tensões: Conceito e aplicações

É comum, ao se analisar um relatório de sondagem, se deparar com solos compostos por várias camadas, cada uma com características e resistência própria. Então, você pode ficar na dúvida de qual dessas camadas é responsável por resistir os esforços induzidos pelas fundações da sua obra. Essa dúvida pode ser respondida através do conceito de bulbo de tensões. Nesse post iremos discutir seu significado e importância na elaboração de projeto de fundações.

Caso você prefira, você pode acompanhar também todo o conteúdo do post através do vídeo abaixo!

Agora, vamos aprender!

Bulbo de Tensões

Como visto no post sobre tensões induzidas, quanto maior a profundidade de um ponto do solo analisado, menor a influência da carga da fundação sobre o mesmo.

Agora que relembramos disso, considere o carregamento de uma fundação e sua influência sobre a massa de solo abaixo dela, como pode ser visto na figura abaixo.

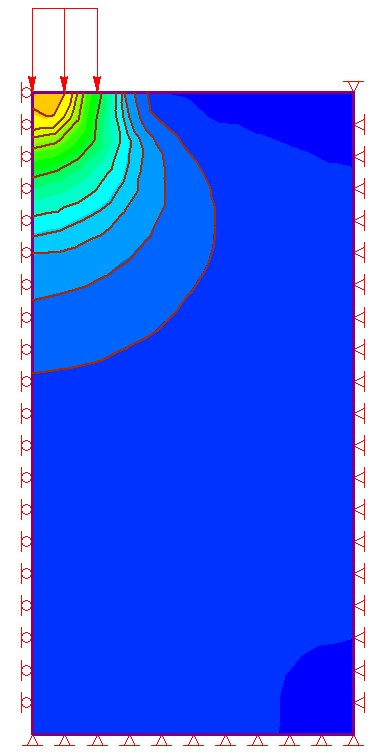
Como era esperado, as maiores tensões (representadas por tons de laranja) encontram-se próximas do ponto de aplicação da carga.

Outra característica que podemos observar é que os locais de solo que apresentam tensões de valores próximos, ou seja, de mesma cor, apresentam formato semelhante a um bulbo.

Mas afinal, o que é um bulbo de tensões?

Bulbo de tensões ou bulbo de pressões é o conjunto de várias curvas de isovalores de tensões verticais no solo induzidas por um carregamento externo.

Podemos representar a magnitude das tensões induzidas por uma fundação, bem como seus pontos de alcance, através do bulbo de tensões, como ilustrado na figura abaixo.

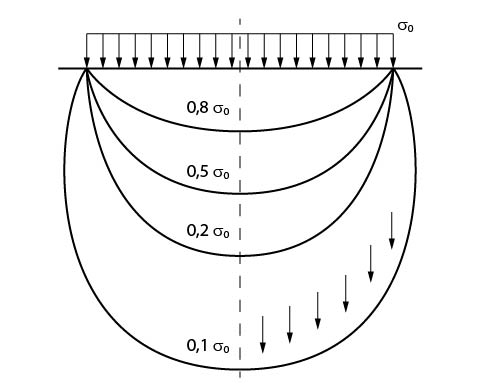
Podemos dizer que a tensão em qualquer ponto no interior da massa de solo limitada por uma curva do bulbo de tensões é superior ao valor de tensão dessa curva.

Ou seja, qualquer ponto no interior do bulbo delimitado pela curva de 0,2\mathrm{\cdot\sigma_0} tem tensão igual ou superior a 0,2\mathrm{\cdot\sigma_0}.

Agora que já entendemos o conceito de bulbo de tensões, vamos às aplicações desse conceito.

Importância do bulbo de tensões

Como comentamos anteriormente, é comum nos depararmos com estudos de sondagem que apontam para solos com várias camadas. Dentre essas camadas, é possível que a camada de maior resistência esteja na superfície.

Logo, é preciso determinar qual o alcance do bulbo de tensões da fundação para saber se a mesma terá efeito sobre a camada de menor resistência.

Inicialmente, precisamos entender que, na prática, para valores de tensão menores que 0,1\mathrm{\cdot\sigma_0}, podemos desconsiderar os efeitos de deformação do solo de fundação.

Então, podemos definir que o bulbo de tensões é delimitado pela curva de isovalor de 0,1\mathrm{\cdot\sigma_0}. Logo, para definirmos qual o alcance do bulbo de uma fundação, basta sabermos a profundidade desse bulbo.

Pelos resultados obtidos de experimentos e simulações computacionais, percebeu-se que quanto maior for a dimensão da fundação, maior a massa de solo afetada pelo bulbo de tensões, logo, maior será sua profundidade.

Chegou-se à conclusão que a profundidade do bulbo de tensões é \mathrm{Z=\alpha\cdot B}, onde B é a menor dimensão da fundação considerada, conforme ilustrado na figura abaixo. Os valores de \mathrm{\alpha} são apresentados na tabela.

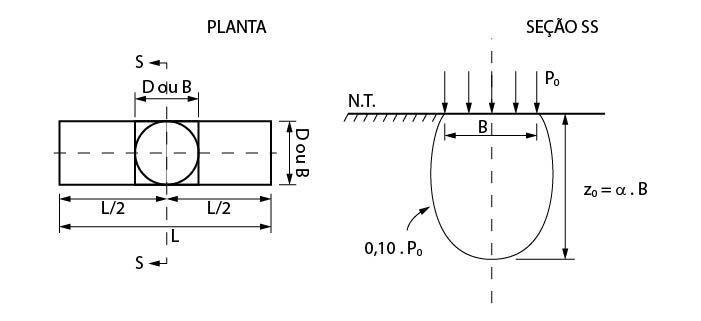
Forma da fundação		\mathrm{\alpha}
Circular ou quadrada		2,0
Retangular (\mathrm{L\cdot B})	1,5	2,5
	2,0	3,0
	3,0	3,5
	4,0	4,0
Infinitamente longa		6,5

Os valores de \mathrm{\alpha} foram obtidos através da teoria da elasticidade e devem ser acrescidos em 20% dos valores da tabela para solos arenosos.

Agora, vamos resolver um exemplo simples para entender a aplicação do bulbo de tensões na prática.

Exemplo prático

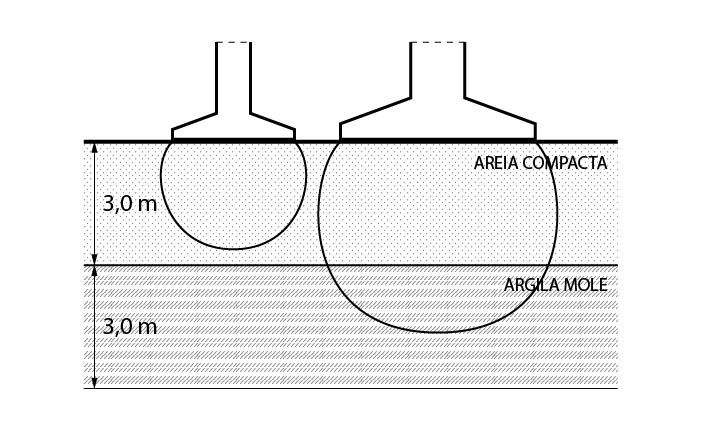
Vamos considerar o perfil de solo ilustrado na figura abaixo.

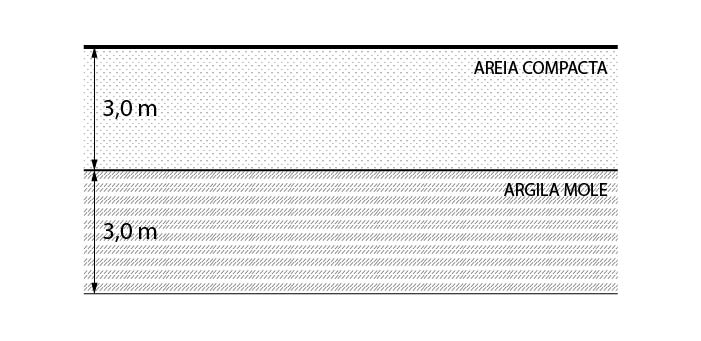
Agora vamos considerar 2 sapatas distintas. A sapata S1 possui dimensões de 1,2m x 1,2m e a sapata S2 possui dimensões de 2,0m x 2,0m.

Podemos perceber, que ao considerar o bulbo de tensões da S1, temos:

\mathrm{Z=\alpha\cdot B=2.0\cdot1.2=2.4 m}

Ou seja, todo o bulbo de tensões da sapata está contido na camada de areia compacta, logo, essa camada é responsável por resistir toda a tensão induzida pela sapata S1.

Já para a sapata S2, temos:

\mathrm{Z=\alpha\cdot B=2.0\cdot2.0=4,0 m}

Logo, para a S2, parte do bulbo de tensões está contido na camada de argila mole. Ou seja, uma parcela das tensões serão resistidas por essa camada, então, será necessária a verificação de resistência à compressão da camada de argila mole, e não somente da camada de areia compacta, como ocorre na sapata S1.

Em outro post nos aprofundaremos mais em como determinar a capacidade de carga de cada camada.

Ficou claro pelo exemplo a importância do conhecimento do conceito do bulbo de tensões?

Agora vamos citar outra situação em que esse conceito é importante, que é no recalque por superposição de pressões.

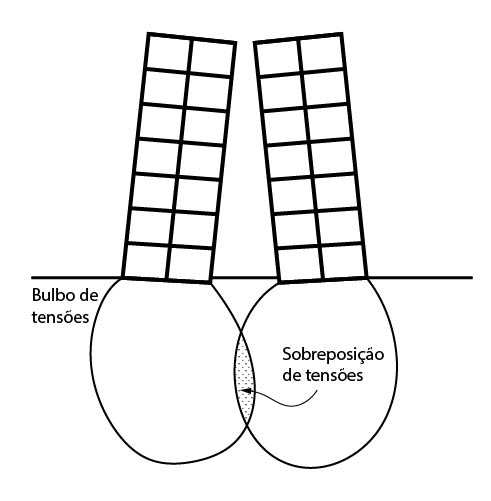
Recalque por superposição de pressão

Quando são construídas edificações de grande carga, ou seja, com grande área de influência do bulbo de tensões, próximas a outras construções de fundações diretas superficiais é comum ocorrer uma sobreposição dos bulbos das edificações.

Caso ocorra essa superposição, ocorrerão recalques nas edificações, principalmente na mais antiga.

Tal recalque pode acarretar o aparecimento de fissuras e trincas nos elementos da construção, podendo afetar sua utilização, e dependendo da magnitude das manifestações patológicas, até mesmo sua segurança.

Conseguiu entender bem o conceito do bulbo de tensões e suas aplicações?

Esperamos que esse post tenha ajudado você a aprimorar seus conhecimentos e sanar suas dúvidas a respeito do tema!

Se você tem interesse pela área de engenharia geotécnica e quer aprender ainda mais, indico os livros Curso Básico de Mecânica dos Solos e Mecânica dos Solos e suas Aplicações. Ambos os livros são de autores nacionais bem conceituados, possuem amplo conteúdo, leitura simples e que podem agregar bastante na sua formação. Além disso, não deixe de seguir nosso blog!

Se ainda ficou com alguma dúvida, deixe nos comentários abaixo!

Até a próxima, pessoal! =)

---

Fonte:

GERSCOVICH, D. M. S. Tensões em solos. Notas de aula. Rio de Janeiro, 2008.

CAPUTO, Homero Pinto. Mecânica dos solos e suas aplicações. Volume 1. 7ª edição. Rio de Janeiro, LTC, 2015.