Para iniciarmos, perda de carga, em Hidráulica, refere-se à perda de energia que um fluido, em uma tubulação sob pressão, sofre em razão de vários fatores como o atrito deste com uma camada estacionária aderida à parede interna do tubo ou em razão da turbulência devido às mudanças de direção do traçado.
A figura abaixo exemplifica a perda de carga em uma tubulação, representada por ΔH.

Existem dois tipos de perdas de carga: as distribuídas e as localizadas. Nesse post, veremos quais as características de cada uma e as principais diferenças entre elas.
Faça bom proveito!
Ah, se preferir assistir uma videoaula sobre o assunto, confira nosso vídeo abaixo. Se não, prossiga com a leitura.
Perda de carga distribuída
Esse tipo de perda de carga ocorre em trechos de tubulação retilíneos e de diâmetro constante.
Ela se dá porque a parede dos dutos retilíneos causa uma perda de pressão distribuída ao longo de seu comprimento que faz com que a pressão total vá diminuindo gradativamente, daí o nome perda de carga distribuída.
A seguir, aprenderemos como calcular essa perda de carga em uma tubulação.
Cálculo da perda de carga distribuída
Abaixo, algumas fórmulas usadas para o cálculo da perda de carga distribuída em uma tubulação para vários tipos de escoamento.
Expressão usando a fórmula universal
\mathrm{Δh=f.(L/D).(v^{ 2 }/2g)}
Onde:
- Δh é a perda de carga distribuída (m);
- f é o fator de atrito (adimensional);
- L é o comprimento da tubulação (m);
- D é o diâmetro da tubulação (m);
- v é a velocidade média do escoamento (m/s);
- g é a aceleração da gravidade (m²/s).
Expressão para o fator de atrito
No caso do escoamento laminar (Re < 2000), o fator de atrito é calculado por:
\mathrm{f=64/Re}
Onde:
- Re é o número de Reynolds (adimensional).
Já se o escoamento for turbulento (Re > 4000), o fator de atrito é calculador por interação da seguinte forma:
\mathrm{\dfrac{1}{\sqrt{f}}=-2.log\left[\dfrac{ε/D}{3,7}+\dfrac{2,51}{Re\sqrt{f}}\right]}
Onde:
- f é o fator de atrito (adimensional);
- ε/D é a rugosidade relativa (adimensional);
- Re é o número de Reynolds (adimensional).
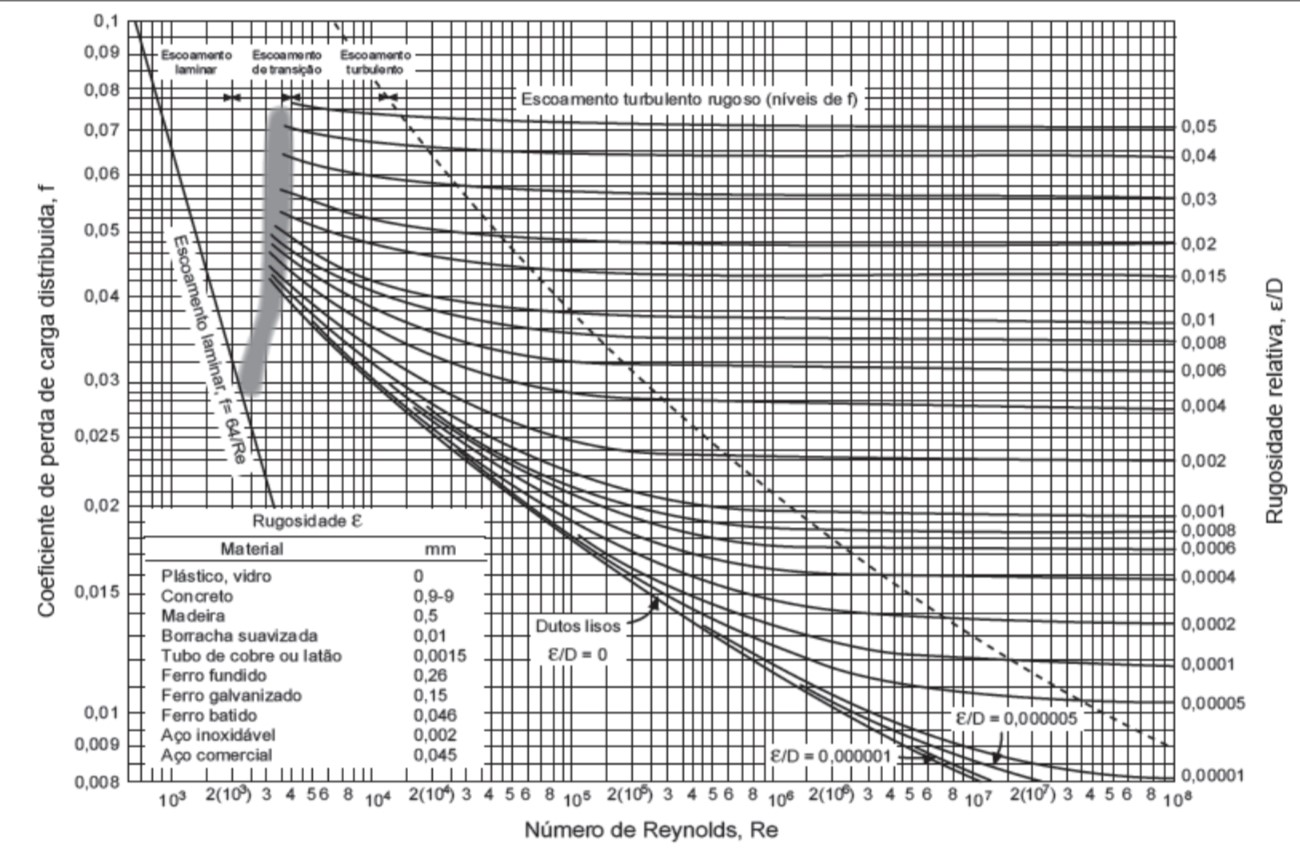
Para facilitar, o gráfico abaixo permite determinar o fator de atrito em função do número de Reynolds e da rugosidade relativa para tubulações comerciais que transportam qualquer líquido.
Expressão usando a fórmula de Chézy
\mathrm{v=C\sqrt{R_{ H }.J}}
Onde:
- v é a velocidade média do escoamento (m/s);
- C é o coeficiente de Chézy (adimensional);
- RH é o reio hidráulico (m);
- J é a perda de carga unitária e é igual a J=Δh/L (m/m).
Fórmula de Chézy com coeficiente de Manning
\mathrm{(nQ/\sqrt{J})= A.(R_H)^{2/3}}
Onde:
- n é o número de Manning (adimensional), tabela 1;
- Q é a vazão do fluido (m³/s);
- J é a perda de carga unitária e é igual a J=Δh/L (m/m);
- L é o comprimento da tubulação (m);
- A é a área molhada (m²);
- RH é o reio hidráulico (m).
Reescrevendo a fórmula acima, temos:
\mathrm{Δh=\left(\dfrac{n.Q}{A.{R_H}^{2/3}}\right)^2L}
Tabela 1 – Número de Manning.
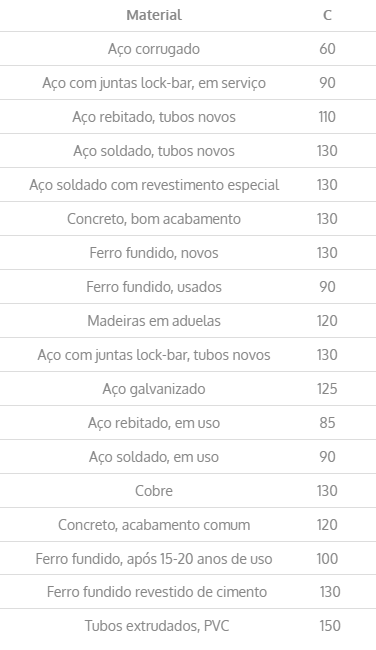
Expressão usando a fórmula de Hazen-Williams
\mathrm{Δh = 10,643 .Q^{1,85}.C^{-1,85}.D^{-4,87}.L}
Onde:
- Δh é a perda de carga distribuída (m);
- Q é a vazão do fluido (m³/s);
- C é o coeficiente de rugosidade (m0,367/s), tabela 2;
- D é o diâmetro da tubulação (m);
- L é o comprimento da tubulação (m).
Tabela 2 – Valores para o coeficiente de rugosidade C.
Perda de carga localizada
A perda de carga localizada ocorre em trechos da tubulação onde há presença de acessórios, sejam eles: válvulas, curvas, derivações, registros ou conexões, bombas, turbinas e outros.
A presença desses acessórios contribui para a alteração de módulo ou direção da velocidade média do escoamento e, consequentemente, de pressão no local, ou seja, age alterando a uniformidade do escoamento.
Dessa forma, há contribuição para o aumento da turbulência no fluido e essa turbulência provoca a perda de carga. Neste caso, a perda de carga é provocada pelos acessórios na tubulação e recebe o nome de perda de carga localizada.
Um fato curioso sobre a perda de carga localizada é que sua influência sobre a linha de energia ocorre tanto a montante como a jusante da localização do acessório presente na tubulação.
A seguir, veremos como calcular essa perda de carga em diversas situações.
Cálculo da perda de carga localizada utilizando a expressão geral
Abaixo, as fórmulas usadas para o cálculo da perda de carga localizada em uma tubulação (para vários acessórios), utilizando a expressão geral da perda de carga localizada, que é a seguinte:
\mathrm{Δh = K.(V^2/2g)}
Onde:
- K é um coeficiente (adimensional) e será estudado em várias situações, a seguir;
- V é uma velocidade de referência (m/s);
- g é a aceleração da gravidade (m²/s).
Expressão da perda de carga localizada para alargamentos e estreitamentos
Alargamento brusco
A mudança de diâmetro de uma tubulação pode ser gradual ou de maneira abrupta.
Quando essa mudança ocorre na forma de um alargamento brusco, a perda localizada se dá pela desaceleração do fluido no trecho. Um exemplo disso é a passagem em aresta viva de uma canalização para um reservatório de grandes proporções.
A equação abaixo é usada para a perda de carga localizada para alargamentos bruscos.
\mathrm{\Delta h}\ =\frac{\left(V1-V2\right)^2}{2g}=\left[1-\left(\frac{A1}{A2}\right)\right]^2\left(\frac{V1^2}{2g}\right)
Onde:
- \mathrm{[1-(A1/A2)^2]=K};
- V1 é a velocidade na seção de menor diâmetro (m/s);
- A1 é a área na seção de menor diâmetro (m²);
- A2 é a área na seção de maior diâmetro (m²).
Estreitamento brusco
Já na contração brusca, o fluido se afasta da fronteira sólida na forma de uma contração do jato e, então se expande para preencher totalmente a seção de menor diâmetro a jusante.
A equação abaixo é usada para a perda de carga localizada para alargamentos bruscos.
\mathrm{Δh = (1/Cc-1)^2.(V2^2/2g)}
Onde:
- \mathrm{(1/Cc-1)^2=K};
- V1 é a velocidade na seção de maior diâmetro (m/s);
- Cc = A0/A2, sendo A0 é área na seção contraída e A2 a área na seção a montante.
A tabela abaixo expressa o valor do fator K em função da relação entre a área de montante e a área de jusante A2/A1:
Tabela 3 – Valor de K para reduções bruscas.
Alargamento ou estreitamento gradual
O coeficiente K, neste caso, depende do ângulo de abertura ou fechamento e da relação de áreas ou diâmetros das seções extremas. Na tabela abaixo, r é o raio de curvatura da redução e D, o seu diâmetro.
Tabela 4 – Valor de K para contração gradual.
Expressão da perda de carga localizada para cotovelos e curvas
Cotovelos e curvas são acessórios que produzem perda de carga localizada devido à mudança de direção no escoamento. Isso ocorre porque os filetes, que tendem a conservar seu movimento retilíneo, são impedidos pela fronteira sólida da conexão, sendo obrigados a mudar de direção.

Dessa forma, essa mudança de direção provoca uma modificação substancial na velocidade e na distribuição da pressão. A parte interna da curva então sofre aumento de pressão e a parte externa, diminuição.
Para a curva circular de raio r e ângulo α, o coeficiente K é dado por:
\mathrm{K =[0,13+0,16(r/D)^{-3,5} ].\sqrt{α/180}}
Onde:
- r é o raio de curvatura médio (m);
- D é o diâmetro (m);
- α é o ângulo de curvatura (graus).
Já para o cotovelo de ângulo α, K é:
\mathrm{K = 67,6.10^{-6}.(α)^{2,17}}
Onde:
- α é o ângulo de desvio (graus).
Valores diversos de K para registro de gaveta
Para o caso de registro de gaveta, cujo processo de fechamento se dá através de uma lâmina vertical, a tabela abaixo apresenta os valores de K em função do grau de fechamento da válvula (a) e seu diâmetro (D), onde a velocidade considerada é a velocidade média do escoamento na seção plena da tubulação.

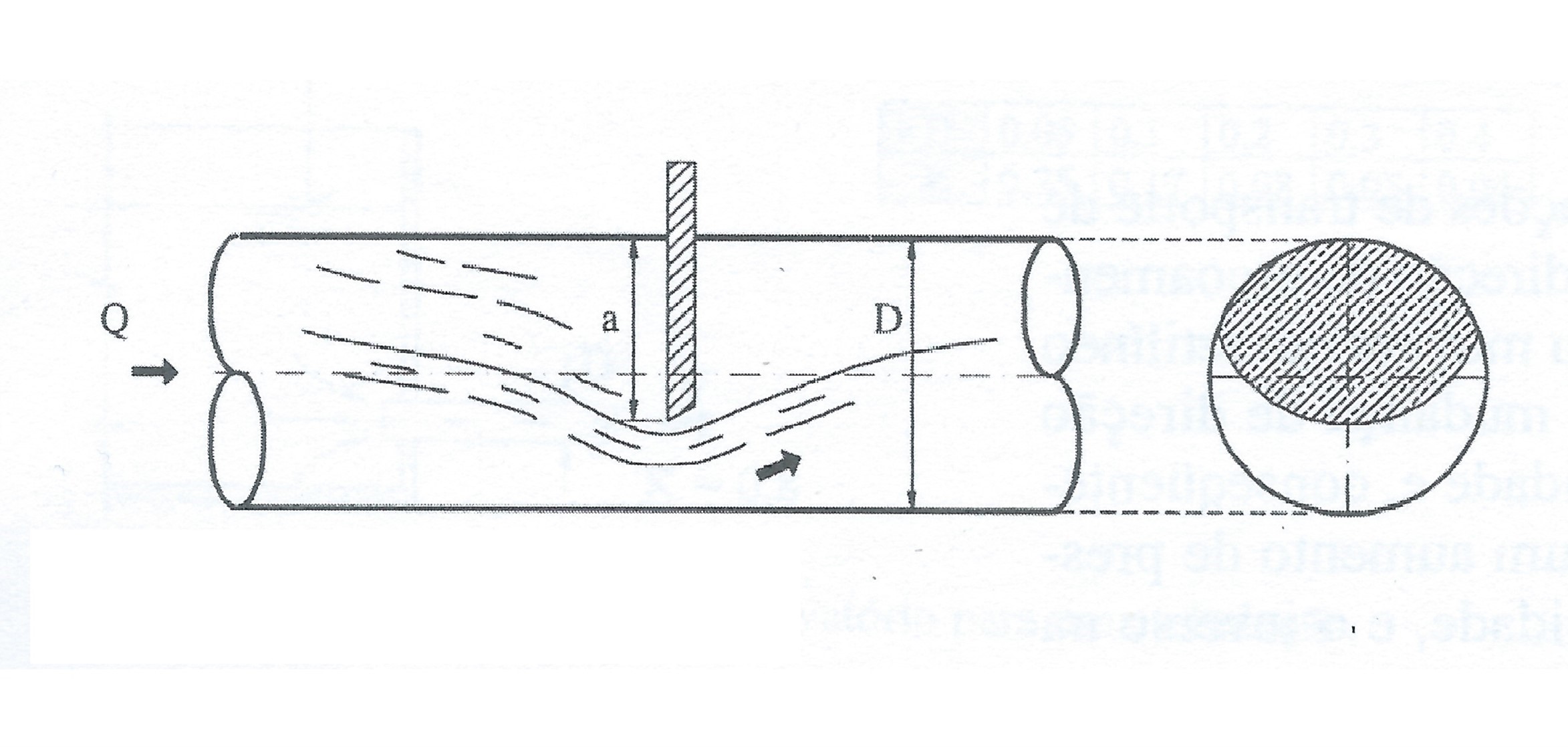
Tabela 5 – Valores de K para registro de gaveta parcialmente fechado.
Valores diversos de K para válvula de borboleta
As válvulas de borboleta são acessórios que fazem o controle da vazão por meio de fixação de um ângulo de abertura.

A tabela abaixo apresenta os valores de K em função do ângulo (α) de abertura da válvula.
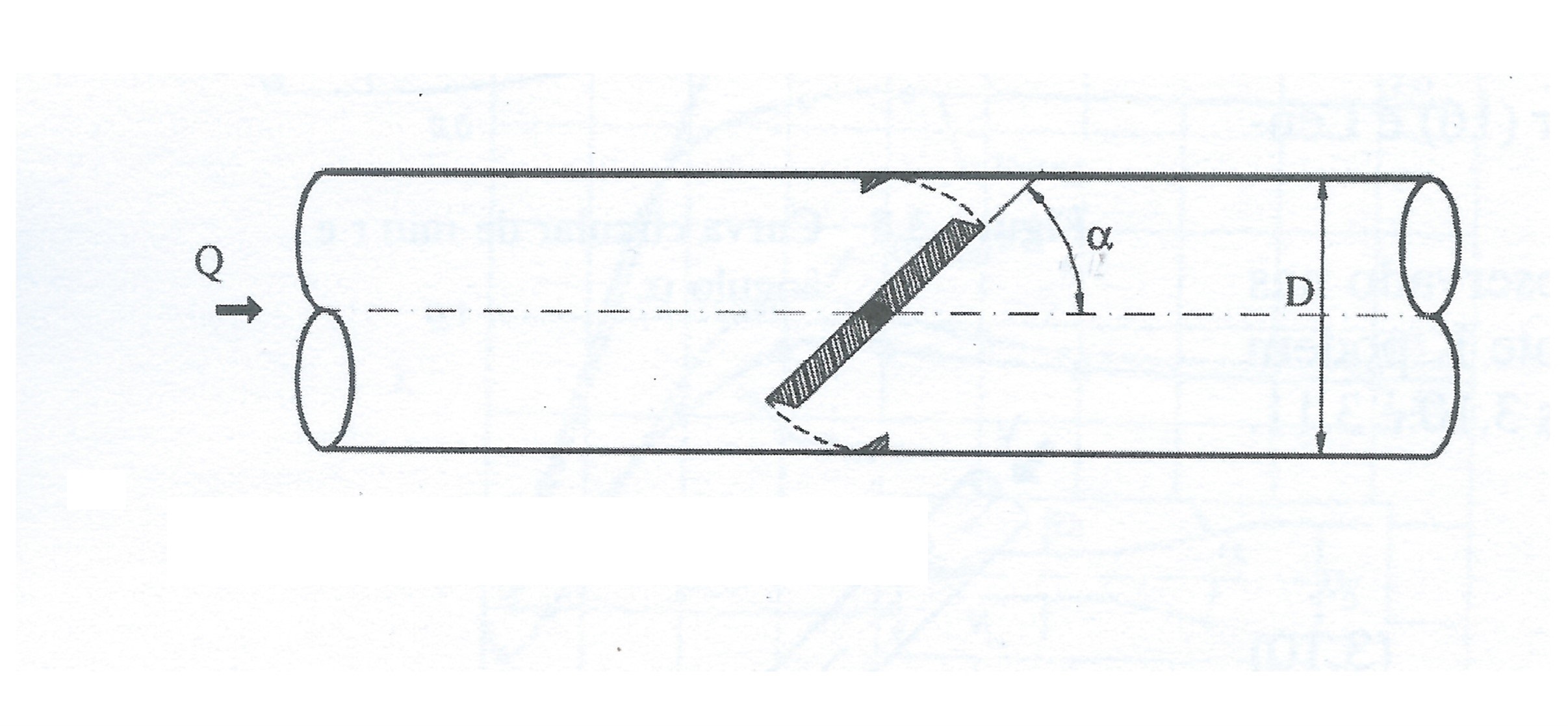
Tabela 6 – Valores de K para válvula de borboleta em função do ângulo de abertura.
Valores diversos de K
A tabela abaixo mostra alguns valores do coeficiente K em outras situações não contempladas acima.
Tabela 7 – Valores do coeficiente K para diversos acessórios.
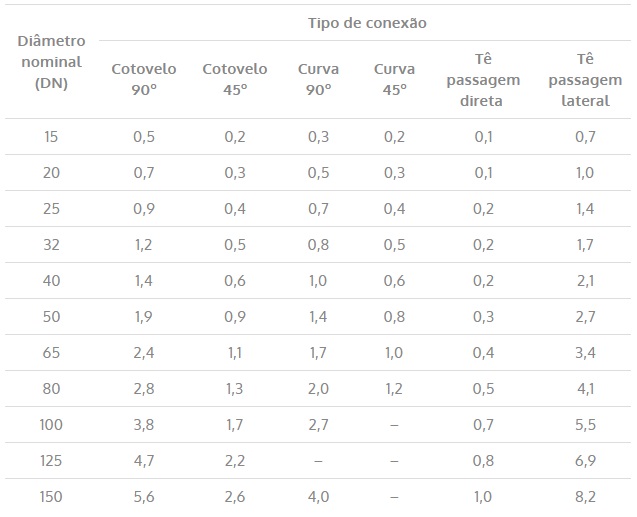
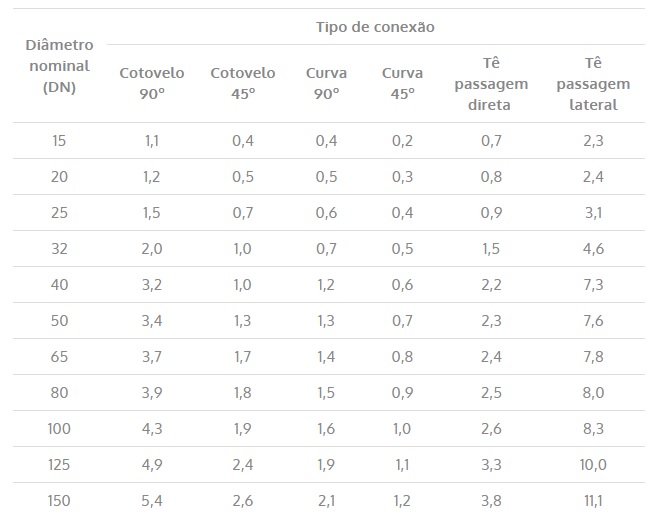
Cálculo da perda de carga localizada pelo comprimento equivalente
Esse segundo método tem o objetivo de facilitar o cálculo da perda de carga localizada simplesmente substituindo os acessórios da instalação (que provocam a perda localizada) por um comprimento de tudo retílineo, de mesmo diâmetro.
Ou seja, esse método transforma virtualmente um valor de perda de carga localizada em distribuída através do uso do comprimento equivalente, sem alterar o valor final da perda de carga total.
Desse modo, o comprimento equivalente pode ser obtido através das tabelas abaixo, retiradas da ABNT NBR 5626:1998, e por fim, podem ser substituídos em qualquer umas das equações de perda de carga distribuída.
Tabela 8 – Comprimento equivalente para tubo rugoso (tubo de aço-carbono,
galvanizado ou não)
Tabela 9 – Comprimento equivalente para tubo liso (tubo de plástico, cobre
ou liga de cobre)
Diferenças entre perda de carga distribuída e localizada
Conforme prometido, agora você já deve saber o que é perda de carga e seus tipos, agora vamos solidificar o que aprendemos nesse post.
A principal diferença entre a perda de carga distribuída e a perda de carga localizada é que a primeira ocorre em trechos retilíneos de uma tubulação, enquanto a segunda, em elementos individuais, ou seja, nos acessórios presentes nela.
Outra diferença importante é que a perda de carda distribuída geralmente é mais sutil que a localizada. Por exemplo, em edificações a perda distribuída tende a ser bem menor que a localizada em virtude do comprimeto das tubulações, já nas tubulações de abastecimento de água ou coleta de esgoto tende a ser maior pelo mesmo motivo.
Desse modo, tanto a perda de carga distribuída como a localizada são somadas e, juntas, contribuem para diminuir a energia de um fluido sob pressão em duto fechado.
Esse post baseou-se, entre outras fontes, nos livros Hidráulica Básica de Rodrigo Melo Porto e Manual de Hidráulica de Azevedo Netto, indicamos para você que tem interesse em se aprofundar mais no assunto.
Temos um post com exercícios, se quiser exercitar o que aprendeu, clique aqui.
Espero que tenhamos lhe ajudado. Se gostou, não deixe de seguir nosso blog para receber mais posts como este!
E se ainda ficou com alguma dúvida, deixe nos comentários abaixo. Estamos à disposição para responder.

Engenheira Civil pela Universidade Federal do Piauí, engenheira de obra, perita judicial e pós-graduanda em Avaliação, Auditoria e Perícias de Engenharia.







Ola bom dia
Tenho algumas perguntas
A perda de carga influência na vazão?
Tipo se a perda de carga foi alta, e a energia disponivel for bem baixa, a vazão será diferente?
E se a energia disponivel for alta, a vazao será diferente?
E se nao influencia, supondo, porque calculamos a perda de carga??
Muito boa as suas perguntas, Luis. Então, eu creio que seja o contrário: a vazão que influencia na perda de carga e esta, por sua vez, influencia a pressão do fluido, que é tão importante quanto a vazão, pois existem limites máximos e mínimos de pressões que podem levar à ruptura de peças ou ao mau funcionamento das instalações.
A perda de carga influencia na vazão, porque a perda de carga e a vazão são grandezas inversamente proporcionais, ou seja, quanto maior a perda de carga, menor a vazão. Quanto menor a perda de carga, maior a vazão. Isso porque a vazão é função da pressão. O exemplo disso, são os bocais. No bocal, a vazão está diretamente ligada à pressão disponível. Se, por exemplo, possuirmos um tanque, com lâmina d’água “x” e um bocal, quando a água sair por esse bocal, a vazão será a maior possível, quando “x” estiver no máximo. Na medida que a água vai saindo, a carga líquida diminuindo e, a vazão, também.
Muito agradecida, Dárcio.