O número de Reynolds, sem dúvidas, é um dos assuntos mais marcantes na engenharia, quando estudamos o comportamento dos fluidos. Contudo, tamanha importância costuma vir seguida de muita confusão e dúvidas. Afinal, há MUITAS maneiras de se classificar os tipos de regime de escoamento.
Além disso, a depender de sua grandeza, inúmeras equações da hidráulica poderão ou não ser aplicadas. Afinal, de nada adianta usar toda a teoria aplicada a um regime viscoso se o fluido possuir comportamento turbilhonar. Concorda?
Pois bem, o meu intuito hoje é te fazer popular naquela rodinha de amigos que se forma 30 minutos antes da prova de Mecânica dos Fluidos ou de Hidráulica!
Nos próximos parágrafos, abordarei o que considero de mais importante sobre o trabalho de Reynods e pertinentes para o momento. Hoje, minha intenção é trazer um artigo completíssimo para você. Então, bora lá?!
Precedentes históricos
A teoria de um número adimensional que prediz o fluxo da massa líquida foi inicialmente introduzida por Sir Stoke. Ele também levou adiante os estudos de Louis Navier, derivando a equação do movimento e adicionando um termo viscoso. Assim, em 1851, foi revelada a equação de Navier-Stokes.
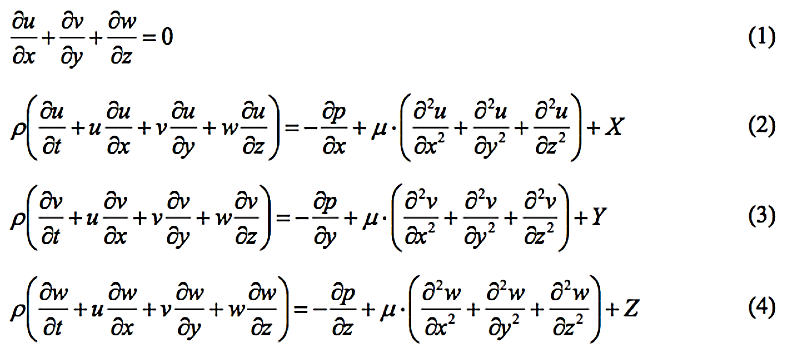
Embora as equações de Navier-Stokes analisassem minunciosamente o fluxo de fluidos, era muito difícil aplicá-las para fluxos arbitrários. Diferentemente, o número de Reynolds poderia prever facilmente o movimento do fluido, dentro do mesmo cenário.
Outros nomes a darem destaque, independentemente, ao estudo do movimento das partículas quanto sua trajetória foram Poiseuille e Hagen. Em 1839, eles observaram, em tubos de pequeno diâmetro, que a pressão era proporcional aos pequenos valores de velocidade.
Assim, para baixas velocidades, a pressão diminuía linearmente ao longo do tubo. Além disso, concluíram que isso deixava de ser verdade para velocidades moderadamente maiores. Neste caso, entrava em cena a influência de um novo fator: a temperatura!

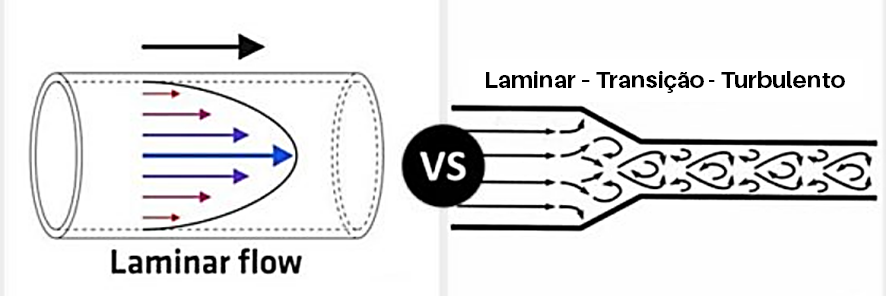
Restou a Osborne Reynolds explicar o que de fato ocorria em tubos de pequeno diâmetro. Definindo, então, a existência de dois regimes de escoamento: laminar (viscoso ou de Poiseuille) e turbulento (ou turbilhonar ou hidráulico).
No regime laminar, os filetes líquidos guardam a sua individualidade e as partículas líquidas que o constituem são as mesmas. Portanto, quando colocados lado a lado – formando a corrente líquida -, esses filetes não permitam partículas entre si.
Enquanto isso, no regime turbulento, a agitação das partículas cria componentes transversais à corrente principal, havendo permuta entre as camadas.
O experimento de Reynolds
Reynolds, por meio do seu trabalho “An experimental investigation of the circumstances which determine whether the motion of water shall be direct or sinuous, and of the law of resistance in parallel channels”, descobriu o número adimensional que prediz o fluxo do fluido com base nas propriedades estáticas e dinâmicas, como velocidade, densidade, viscosidade dinâmica e características do fluido.
Conforme o artigo, o adimensional descoberto por Reynolds era adequado para prever o fluxo de escoamento. A aplicabilidade desse parâmetro varia desde a água em tubulações hidráulicas até o fluxo de ar sobre um aerofólio.
Ele conduziu estudos experimentais para examinar a relação entre a velocidade e o comportamento do fluxo de fluidos. Em seu projeto, Reynolds injetou na corrente líquida transparente um filete de líquido colorido e de mesma densidade.
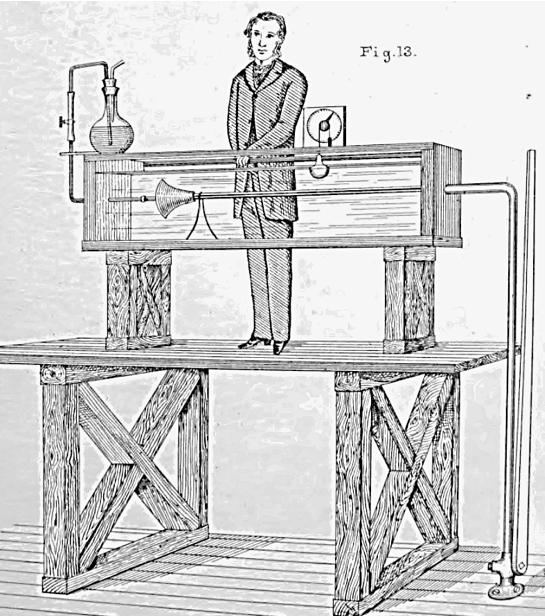
Assim, no regime laminar, o filete manteve a sua individualidade e pôde ser visualizado como se fosse um filete sólido. Cada camada da massa líquida desliza suavemente sobre uma camada adjacente.
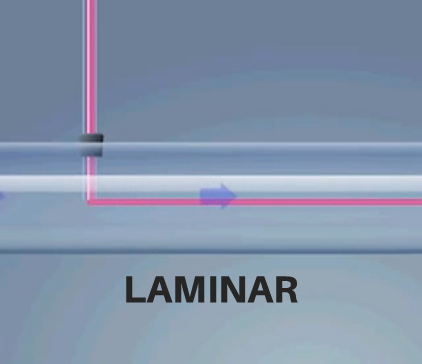
Por outro lado, no regime turbulento ocorreu um fenômeno diverso. O filete colorido se misturou completamente com o líquido transparente, dando a ele uma coloração uniforme e homogênea.
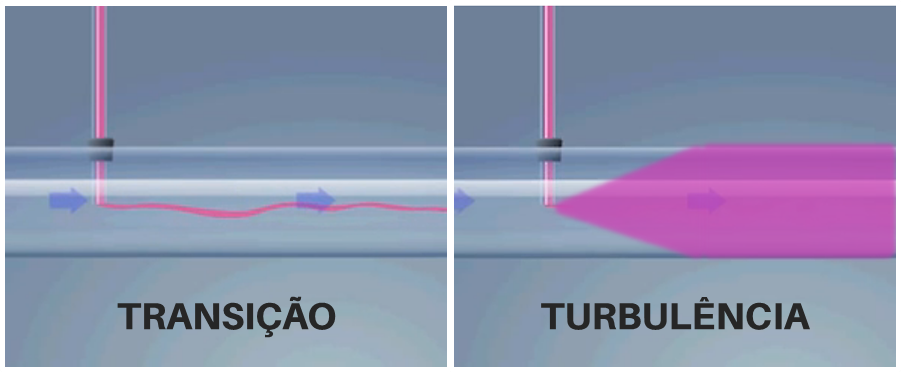
É de se notar, ainda, que o mesmo pode ocorrer no alargamento/estreitamento da seção de uma tubulação. Sendo a área transversal inversamente proporcional à velocidade, é notável o seguinte caso abaixo.
O número de Reynolds
Foi em 1883 que Reynolds demonstrou que a transição de regimes – do laminar para o turbulento – dependia de parâmetros definidos. Tais como velocidade média V da corrente líquida, da viscosidade do líquido ν e do diâmetro D do tudo.
Esta relação, mais tarde, ficou conhecida mundialmente pelo adimensional referido como “número de Reynolds” em sua homenagem (Re).
O número de Reynolds é a razão entre forças inerciais e forças viscosas. Também pode ser visto como uma razão de forças de cisalhamento turbulentas e forças de cisalhamento viscoso. Um número “crítico” de Reynolds distingue entre regimes de fluxo, como fluxo laminar ou turbulento em tubulações, na camada limite ou em torno de objetos imersos. O valor particular depende da situação.
\mathrm{Re = \dfrac{\textbf{Resistência inercial}}{\textbf{Resistência viscosa}}}
Resistência inercial, como o nome indica é a força devido ao momento do fluido. Isso geralmente é expresso na equação do momento pelo termo (ρv)v. Então, quanto mais denso é o fluido, e quanto maior sua velocidade, mais momentum (inércia) ele tem. Forças de inércia tendem a afastar as partículas da camada em que se movimentam.
Como na mecânica clássica, uma força capaz contrabalançar essa força inercial é a força de atrito (tensão de cisalhamento), interna. No caso do fluxo de fluido, isso é representado pela lei de Newton:
\mathrm{\tau_x = \mu \dfrac{dv}{dy}}
Ou
\mathrm{\tau_x = \mu \dfrac{v_x}{D}}
Assim, isso depende apenas da viscosidade e gradiente de velocidade. Já as forças inerciais são o que dá origem à pressão dinâmica. Essa resistência viscosa tende a manter as camadas movendo-se suavemente uma sobre a outra. Como o Número Reynolds é pela razão entre essa pressão dinâmica e a tensão de cisalhamento, expressa-se:
\mathrm{Re = \dfrac{{\rho}vD}{\mu}}
Então, Re = ρvD / μ, é uma medida de qual força predomina para uma condição de fluxo particular. Portanto, as forças inerciais são o que dá origem à pressão dinâmica. Outra maneira de olhar para o Número Reynolds é pela razão:
\mathrm{Re =\dfrac{vD}{\nu}}
OBS: Caso o tubo seja cilíndrico, o diâmetro hidráulico D é aceito como o diâmetro real da tubulação. Além disso, a forma de um tubo ou canal pode variar (por exemplo, quadrado, retangular, etc.). Nesses casos, o diâmetro hidráulico é determinado com base no raio hidráulico, tal que: \mathrm{\mathbf{D_H=\frac{4Am}{Pm}=4R_H}}
Resultados relacionados ao número de Reynolds
Em números muito altos de Reynolds, o movimento do fluido faz com que os redemoinhos se formem e causem fenômenos de turbulência. Quando as forças viscosas são suficientemente altas para que qualquer distúrbio seja suavizado, o fluxo laminar prevalece nos tubos. Quando a velocidade aumenta, as forças de inércia aumentam e as partículas são empurradas para cima a partir do caminho mais suave.
Enquanto o número de Reynolds for inferior a 2.300, o FLUXO LAMINAR prevalece nos tubos. O fator de atrito no fluxo também é encontrado para ser uma função do número de Reynolds (no fluxo laminar, f = 64 / Re). Já para casos em que o número de Reynolds supera 2.400, o fluxo será dado como TURBULENTO. E, portanto, a faixa de valores entre esses parâmetros será considerada de TRANSIÇÃO.
A camada limite em fluxos externos
Em 1914, o cientista alemão Ludwig Prandtl descobriu a camada limite, que é parcialmente função do número de Reynolds, cobrindo a superfície através de regimes laminares, turbulentos e de transição.
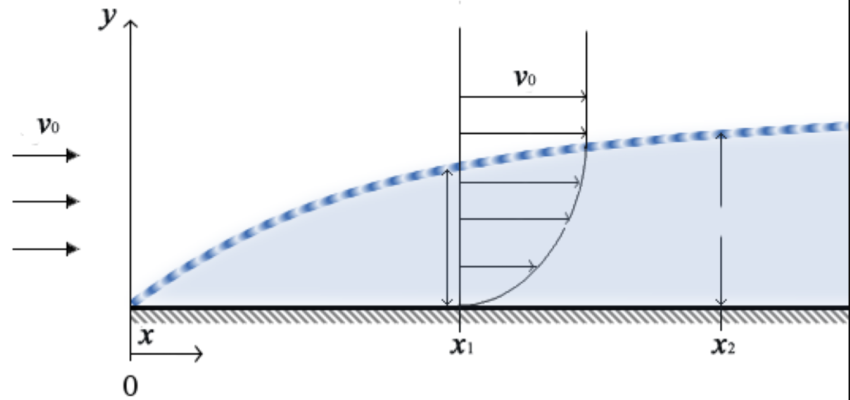
Considere um fluido escoando por uma superfície livre, tal como uma placa de pequena espessura. Em razão do princípio da aderência, a velocidade junto à superfície da placa tende a ser zero. Assim, considerando que haja inicialmente um fluxo uniforme V0 no início desse escoamento, logo ele sofrerá os efeitos dessa aderência.
Portanto, passa-se a existir um gradiente de velocidades ao longo da transversal. Assim, as camadas com velocidade V0 se distanciarão da superfície de contato.
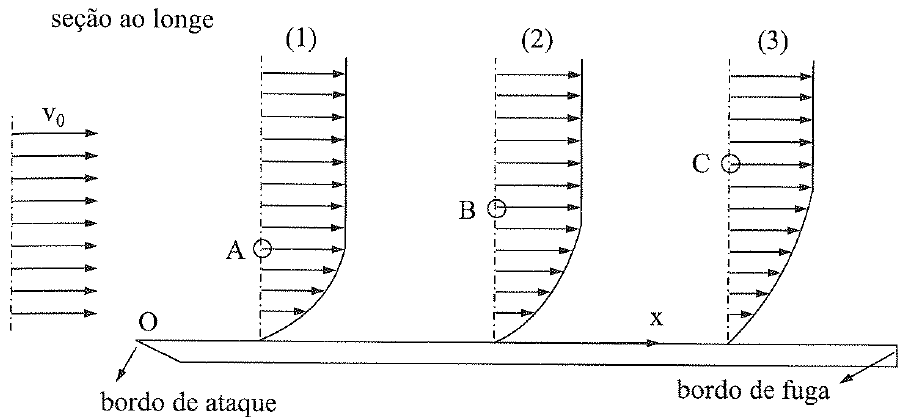
Surge, então, uma zona que não sofrerá qualquer influência da aderência e outra cujas velocidades serão menores que a inicial. É essa região que chamaremos de “camada limite”.
Logo, é a região em que forças de atrito retardam o fluido de sua velocidade externa para um completo repouso. Já a zona acima é chamada de “fluido livre”
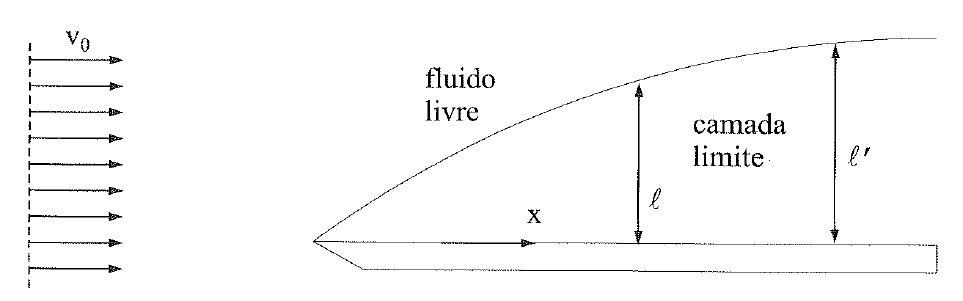
Conforme Franco Brunetti, quando Re>5\times 10^5 o escoamento na camada limite passa de laminar para turbulento.
O fluxo sobre uma superfície plana é mostrado na figura abaixo com regimes em que xc é o comprimento crítico para a transição, L é o comprimento total da placa e u é a velocidade do fluxo da corrente livre.
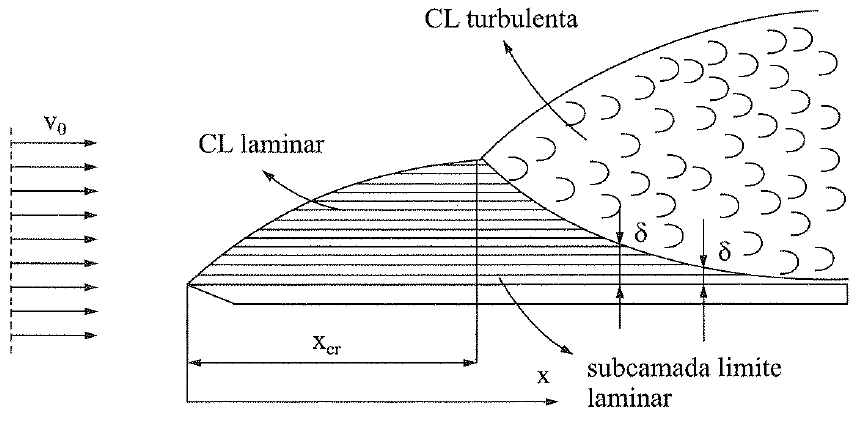
A camada limite em condutos forçados
O raciocínio aqui não muda, a única diferença é que agora o princípio da aderência se manifestará em mais pontos. Assim, como estamos tratando de um conduto forçado, a superfície ficará mais delimitada pelo princípio da aderência.
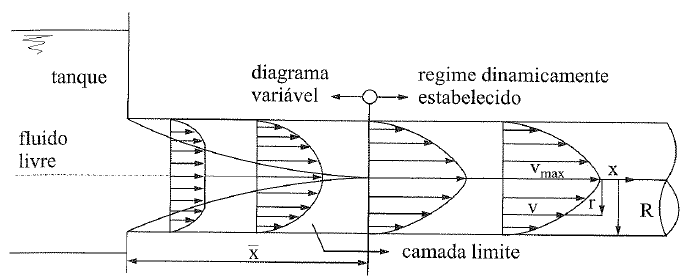
A camada limite cresce até preencher o conduto, deixando-o sem superfície livre ao longo de seu comprimento. Se o preenchimento do conduto ocorre enquanto a camada limite for laminar, então todo o escoamento será laminar. Pois as demais velocidades sempre serão menores que a inicial. Estando a velocidade máxima dentro do valor laminar, todas as demais estarão garantidas dentro desse escoamento. Assim, seu valor será dado por:
\mathrm{V=V_\mathrm{máx}[1-(\dfrac{r}{R})^{2}]}
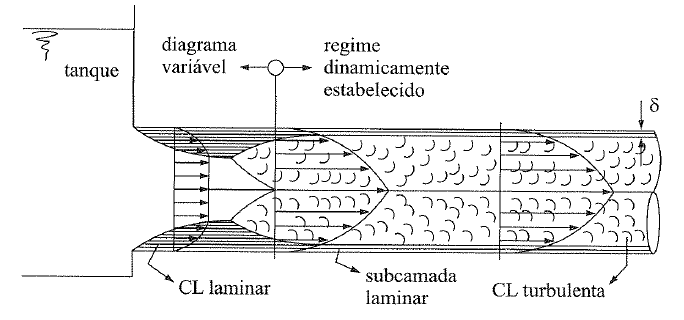
Caso seja turbulento (mais comum), sua velocidade será:
\mathrm{V=V_\mathrm{máx}[1-(\dfrac{r}{R})]^{1/7}}
Grande e pequeno número de Reynolds
Enquanto Re → ∞, os efeitos viscosos são supostamente desprezíveis quando os termos viscosos nas equações de Navier-Stokes são descartados. A forma simplificada das equações de Navier-Stokes – chamadas de equações de Euler – pode ser especificada da seguinte maneira:
\mathrm{\dfrac{D\rho}{Dt}=-\rho\bigtriangledown \times v}
\mathrm{\dfrac{Dv}{Dt}=-\dfrac{\bigtriangledown p}{\rho}+g}
\mathrm{\dfrac{De}{Dt}=-\dfrac{p}{\rho}\bigtriangledown +v}
Onde ρ é densidade, v é velocidade, p é pressão, g é aceleração gravitacional e e é a energia interna específica. Embora os efeitos viscosos sejam relativamente importantes para os fluidos, o modelo de fluxo invíscido fornece um modelo matemático confiável para prever um processo real para alguns casos específicos.
Por exemplo, o fluxo externo de alta velocidade sobre corpos é uma aproximação amplamente usada onde a abordagem invíscida se encaixa de maneira razoável.
Enquanto Re≪1, os efeitos inerciais são considerados desprezíveis e os termos relacionados nas equações de Navier-Stokes podem ser descartados. A forma simplificada das equações de Navier-Stokes é chamada de fluxo Stokes (creeping flow):
\mathrm{\mu\bigtriangledown^{2} -\bigtriangledown p + f = 0}
\mathrm{\bigtriangledown \times v = 0}
Onde v é a velocidade do fluido, \bigtriangledown p é o gradiente de pressão, μ é a viscosidade dinâmica e f é a força do corpo aplicada. Tendo efeitos viscosos tangíveis, o fluxo de Stokes é uma abordagem adequada que pode ser usada para investigar, por exemplo, o fluxo de lava, o nado de micro-organismos, fluxo de polímeros, lubrificação, etc.
Palavras finais
Ufa! Chega, né?! Bem, espero que este artigo sirva de base para seus estudos e trabalhos acadêmico, bem como para a sua vida. (Por que não?)
Busquei extrair o MÁXIMO de informações possíveis que nem sempre é abordado em uma única bibliografia. Assim, se tiver alguma sugestão ou dúvida, só me chamar.
Abraços do João!

Engenheiro Civil, ex-Griffon (MWSU), SunDevils (ASU), judoca e pseudo-nadador. Pós-graduando em Gerenciamento de Obras e Tecnologia da Construção.
Gostei; parabéns!!!
Forte abraço!
me ajudou muito, top
Show de bola, Alexandre! Feliz em saber.
Muito bom me ajudou muito