Você saberia como proceder caso estivesse dimensionando uma viga de concreto e a mesma apresentasse uma profundidade de linha neutra superior aos limites estabelecidos por norma? Uma possível solução seria aumentar a altura da viga. Contudo, e se essa alternativa, devido a limites arquitetônicos, não for viável? Nesse post você irá aprender uma solução para a situação apresentada: calcular a viga com a utilização de armadura dupla, ou seja, uma armadura adicional na região comprimida da viga.
Conceito de armadura dupla
Primeiramente, vamos entender o que é armadura dupla e sua base teórica.
Imagine uma situação em que o momento solicitante em uma seção é suficiente para atingir uma profundidade de linha neutra igual ao limite de norma (\mathrm{0,45 \cdot d} para concretos até 50 MPa e sem redistribuição de momentos).
O momento gerado pelo binário força de tração no aço e de compressão no concreto é igual ao momento solicitante. Além disso, uma vez que não temos esforços axiais, as forças de compressão no concreto e tração no aço tem a mesma intensidade.
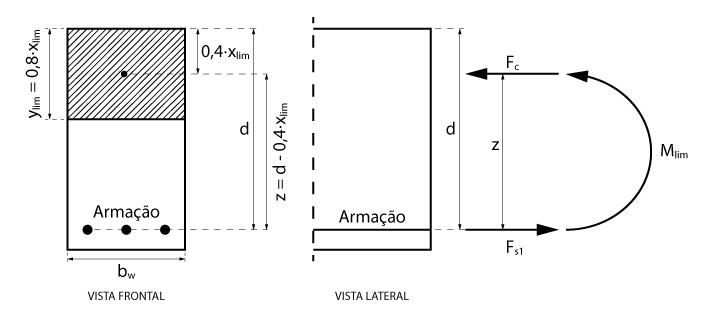
Você sabe o que aconteceria caso fosse adicionado mais momento à seção?
A fim de equilibrar o novo momento, seria necessário que o binário também se eleve para que o equilíbrio entre esforços externos e internos seja mantido, correto?
Com intuito de elevar a força de tração, basta adicionar mais área de aço na região tracionada da viga e para elevar a força de compressão, o processo natural seria a linha neutra descer, dessa forma apresentando mais concreto comprimido. Mas lembre-se que a linha neutra não pode baixar, uma vez que a mesma já atingiu os limites estabelecidos por norma.
Sabendo que a linha neutra já está no seu limite, a solução, denominada de armadura dupla, é adicionar área de aço na região comprimida. Assim sendo, a necessidade de elevação da força de compressão é aplicada no aço e não no concreto, não sendo necessário que a linha neutra abaixe.
Equacionamento
A imagem abaixo resume o exposto nos parágrafos anteriores, em que, um momento que levaria a uma linha neutra fora dos limites é dividido é duas parcelas.
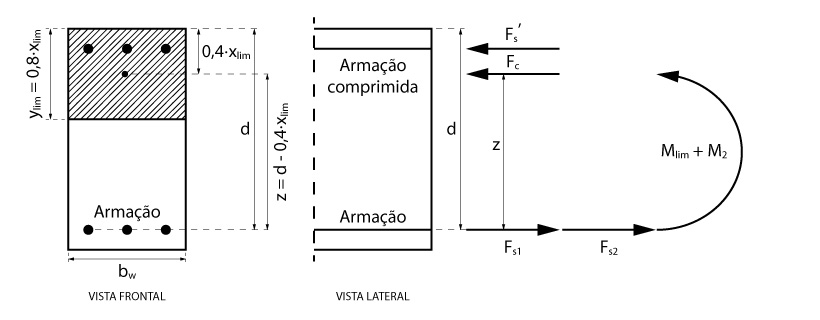
Momento limite para armadura simples
Em primeiro lugar, vamos calcular o \mathrm{M_{lim}} resistido para o caso da seção estar trabalhando no limite da linha neutra (\mathrm{0,45 \cdot d} para concretos até 50 MPa e sem redistribuição de momentos)
Em seguida, calcula-se a armadura necessária para resisti-lo (\mathrm{A_{s1}}) e o momento restante (\mathrm{M_2 = M_{Sd} - M_{lim}}).
Com intuito de deixarmos o desenvolvimento para situações mais usuais, vamos considerar o limite para concretos de até 50 MPa. Uma vez que a posição da linha neutra já é conhecida, é imediato o cálculo da força atuante no concreto:
\mathrm{F_c = 0,85 \cdot f_{cd} \cdot b_w \cdot 0,8 \cdot x_{lim}}
\mathrm{F_c = 0,85 \cdot f_{cd} \cdot b_w \cdot 0,8 \cdot 0,45 \cdot d}
Vamos agora simplificar a equação acima:
\mathrm{F_c = 0,306 \cdot f_{cd} \cdot b_w \cdot d}
O momento limite é calculado simplesmente multiplicando essa força no concreto pelo braço de alavanca entre o mesmo e a armadura:
\mathrm{M_{lim} = F_c \cdot z}
\mathrm{M_{lim} = F_c \cdot (d - 0,4 \cdot x_{lim})}
Vamos agora substituir o valor da linha neutra limite:
\mathrm{M_{lim} = F_c \cdot (d - 0,4 \cdot 0,45 \cdot d)}
\mathrm{M_{lim} = F_c \cdot (d - 0,18 \cdot d)}
Por fim, chegamos na equação que iremos utilizar para obtenção do momento limite para utilização da armadura simples:
\mathrm{M_{lim} = F_c \cdot 0,82 \cdot d}
\mathrm{M_{lim} = 0,251 \cdot b_w \cdot d^2 \cdot f_{cd}}
Em seguida, podemos calcular a área de aço necessária para resistir ao momento limite de armadura simples:
\mathrm{A_{s1} = \dfrac{M_{lim}}{z_{lim} \cdot f_{yd}}}
\mathrm{A_{s1} = \dfrac{M_{lim}}{0,82 \cdot d \cdot f_{yd}}}
Momento restante para armadura dupla
O momento restante será resistido pelo segundo binário \mathrm{F_{s2}} e \mathrm{F_s '} e vale:
\mathrm{M_2 = M_{Sd} - M_{lim}}
O braço de alavanca do segundo binário e a área de aço a ser adicionada na região inferior valem:
\mathrm{z_2 = d - d'}
\mathrm{M_2 = F_{s2} \cdot z_2}
Uma vez que, a armação inferior está escoando, temos a relação entre a força atuante no aço e a área de aço:
\mathrm{F_{s2} = A_{s2} \cdot f_{yd}}
Em seguida, podemos combinar as equações apresentadas acima:
\mathrm{A_{s2} = \dfrac{M_2}{z_2 \cdot f_{yd}}}
\mathrm{A_{s2} = \dfrac{M_2}{(d - d') \cdot f_{yd}}}
Repare que, para calcularmos os valores de \mathrm{A_{s1}} e \mathrm{A_{s2}} consideramos \mathrm{f_s = f_{yd}}. Se está familiarizado com os domínios de deformação, se lembrará que essa profundidade de linha neutra limite ocorre no domínio 3, garantindo assim que a armação inferior tenha escoado.
Em contrapartida, para armadura que será adicionada na zona comprimida não existe essa garantia de escoamento. Sabendo que o para o domínio 3 o encurtamento no concreto vale 3,5 ‰, é possível calcularmos a deformação na armadura comprimida.
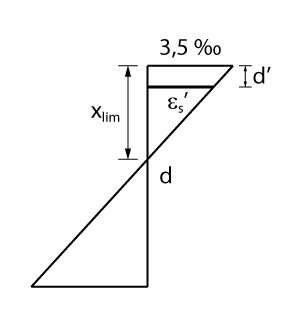
\mathrm{\epsilon_s ' = \dfrac{0,0035 \cdot (x_{lim} - d')}{x_{lim}}}
\mathrm{\epsilon_s ' = \dfrac{0,0035 \cdot (0,45 \cdot d - d')}{0,45 \cdot d}}
Em seguida, com a deformação calculada, o próximo passo é obter a tensão atuante da armadura:
\mathrm { f_s ' = \left\{ \begin{array}{ll} 21.000 \; \dfrac{kN}{cm^2} \cdot \epsilon_s ' \text{; se } \epsilon_s ' < \epsilon_{yd} \\ f_{yd} \text{; se } \epsilon_s ' \geq \epsilon_{yd} \end{array} \right. }
Por fim, a armação adicionada na região superior será:
\mathrm{A_s ' = \dfrac{M_2}{(d - d') \cdot f_s '}}
Exemplo aplicado
A fim de aplicarmos a teoria sobre armadura dupla, vamos dimensionar uma viga já resolvida anteriormente de 14 cm de largura por 40 cm de altura submetida agora a um momento fletor acima do anterior, valendo \mathrm{M_{Sk} = 65 \; kN \cdot m}. Será considerado um concreto de 20 MPa, aço CA50 (\mathrm{f_{yk} = 500 \; MPa}) e um cobrimento de 2,5 cm.
Caso você prefira aprender através de videoaulas, você pode acompanhar a resolução da questão pelo vídeo abaixo:
Primeiramente, vamos calcular o momento fletor de cálculo:
\mathrm{M_{Sd}=\gamma_f \cdot M_{Sk}}
\mathrm{M_{Sd}=1,4 \cdot 65 = 91 \; kN \cdot m}
Vamos considera barras de 25 mm com armadura longitudinal (a favor da segurança) e estribos de 5,0 mm para calcularmos a altura útil da seção:
\mathrm{d = h - c - \phi_t - \dfrac{\phi}{2}}
\mathrm{d = 40 - 2,5 - 0,5 - \dfrac{2,5}{2} = 35,75 \; cm}
Obtenção da posição linha neutra
Antes que passemos para os cálculos expostos nessa publicação, vamos verificar primeiro a profundidade da linha neutra:
\mathrm{k=\dfrac{M_{Sd}}{b_w \cdot f_{cd}}}
\mathrm{k=\dfrac{9100}{14 \cdot \dfrac{2}{1,4}} = 455 \; cm^2}
O valor de \mathrm{k} é uma simplificação explicada na publicação sobre aplicações da formulações de vigas submetidas à flexão.
\mathrm{x = \dfrac{0,68 \cdot d \pm \sqrt{0,4624 \cdot d^2 - 1,088 \cdot k}}{0,544}}
\mathrm{\dfrac{24,31 \pm \sqrt{0,4624 \cdot (35,75)^2 - 495,04}}{0,544}}
Enfim chegamos nas duas soluções dessa equação do segundo grau:
\mathrm { x = \left\{ \begin{array}{ll} 62,69 \; cm \\ 26,68 \; cm \end{array} \right. }
Visto que o exemplo trata de uma viga submetida à flexão simples (sem presença de esforços normais), não seria possível uma linha neutra fora da seção. Assim sendo, o resultado \mathrm{x = 62,69} \; cm pode ser descartado.
A linha neutra de 26,68 cm (\mathrm{\dfrac{x}{d} = \dfrac{26,68}{35,75} = 0,75}) supera o limite estabelecido na norma para garantir a ductilidade da peça. Dessa forma, teríamos duas soluções imediatas: a primeira, aumentar a altura da viga, caso possível; a segunda, dimensionar a viga com armadura dupla.
Supondo a existência de limitações arquitetônicas, vamos partir para a segunda solução.
Cálculo da armação e do momento limite
Uma vez que decidimos pela utilização de armadura dupla, vamos calcular o momento limite resistido por essa seção sem a utilização de armadura de compressão, ou seja, com armadura simples:
\mathrm{M_{lim} = 0,251 \cdot b_w \cdot d^2 \cdot f_{cd}}
\mathrm{3,51 \cdot (35,75)^2 \cdot \dfrac{2}{1,4} = 6415,87 \; kN \cdot cm}
Assim sendo, fica clara a necessidade de utilizar armadura de compressão, uma vez que, o momento limite de 6415,87 kN.cm é inferior ao momento solicitante de 9100 kN.cm.
Vamos agora calcular a área de aço tracionada responsável por resistir ao momento limite:
\mathrm{A_{s1} = \dfrac{M_{lim}}{0,82 \cdot d \cdot f_{yd}}}
\mathrm{A_{s1} = \dfrac{6415,87}{0,82 \cdot 35,75 \cdot \dfrac{50}{1,15}} = 5,03 \; cm^2}
Cálculo da armadura dupla (armadura tracionada)
Em primeiro lugar, vamos calcular o momento que ainda falta ser resistido:
\mathrm{M_2 = M_{Sd} - M_{lim}}
\mathrm{9100 - 6415,87 = 2684,13 \; kN \cdot cm}
Em seguida, obtemos o braço de alavanca para a armadura dupla inferior:
\mathrm{z_2 = d - d'}
\mathrm{z_2 = 35,75 - 4,25 = 31,5 \; cm}
Por fim, chegamos na área de aço que deverá ser adicionada a \mathrm{A_{s1}}:
\mathrm{A_{s2} = \dfrac{M_2}{z_2 \cdot f_{yd}}}
\mathrm{\dfrac{2684,13}{31,5 \cdot \dfrac{50}{1,15}} = 1,96 \; cm^2}
Dessa forma, a área de aço na região inferior vale:
\mathrm{A_s = A_{s1} + A_{s2} = 6,99 \; cm^2}
Cálculo da armadura dupla (armadura comprimida)
Por fim, só nos falta calcular a armadura dupla que será adicionada na região comprimida. Para isso, em primeiro lugar, iremos verificar a deformação e tensão para a armadura comprimida:
\mathrm{\epsilon_s ' = \dfrac{0,0035 \cdot (0,45 \cdot d - d')}{0,45 \cdot d}}
\mathrm{\dfrac{0,0035 \cdot (16,09 - 4,25)}{16,09} = 0,00258}
Visto que a deformação do aço comprimido é superior a deformação de escoamento (\mathrm{\epsilon_{yd} = 0,00207}), a tensão atuante no mesmo é igual a tensão de escoamento. Portanto, a área de aço comprimida vale:
\mathrm{A_s ' = \dfrac{M_2}{(d - d') \cdot f_s '} = \dfrac{M_2}{(d - d') \cdot f_{yd}}}
\mathrm{A_s ' = \dfrac{2684,13}{(31,5) \cdot \dfrac{50}{1,15}} = 1,96 \; cm^2}
Esse resultado já era esperado, uma vez que as forças no binário adicional são iguais (\mathrm{F_{s2} = F_s '}) e as duas estão submetidas à tensão de escoamento, as áreas \mathrm{A_{s2}} e \mathrm{A_s '} também serão iguais.
Apenas para conferir o resultado encontrado, vamos resolver o mesmo exemplo utilizando nossa Calculadora de Vigas aqui do blog:
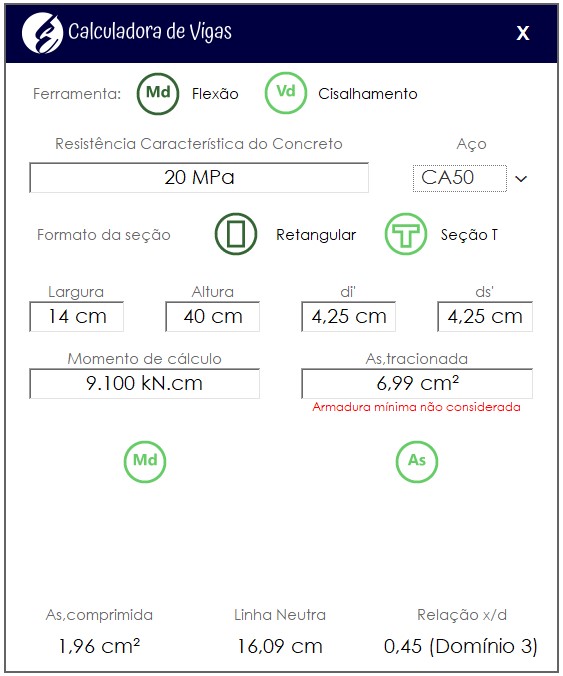
Caso queira baixar sua Calculadora gratuitamente, basta solicitar através do formulário abaixo:
[formulario-calculadora-flexao]Assim sendo, poderemos por fim detalhar a seção transversal da viga em questão:
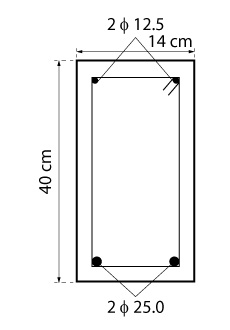
Dimensionamento através de softwares
Ao utilizar softwares comerciais esses dimensionamentos de armaduras duplas, assim como demais verificações, tornam-se automáticos.
Softwares comerciais aumentam a produtividade do engenheiro calculista ao realizar essas verificações automáticas, desde que configurados corretamente. Essa é uma das principais diferenças dos profissionais que se destacam no mercado.
Se você tem interesse em ganhar mercado na área de cálculo estrutural, recomendo bastante o curso Essencial em Concreto Armado do professor Rangel Lage em que você irá aprender a utilizar o software TQS (na minha opinião, o melhor software do mercado) passando por TODAS as etapas (desde a concepção estrutural até elaboração das pranchas) necessárias para o desenvolvimento de um projeto completo.
Considerações finais
Nesse post você aprendeu a dimensionar seções de concreto armado submetidas flexão simples utilizando também uma armadura de compressão. Se você gostou desse texto sobre armadura dupla, não esqueça de compartilhar com seus amigos!
Fonte:
ARAÚJO, J. M. Curso de Concreto Armado. Rio Grande: Editora Dunas, 2014. v. 1
ASSOCIAÇÃO BRASILEIRA DE NORMAS TÉCNICAS. NBR 6118: Projeto de estruturas de concreto – Procedimento. Rio de Janeiro, 2014.
CARVALHO, R. C.; FIGUEIREDO FILHO, J. R. Cálculo e Detalhamento de Estruturas Usuais de Concreto Armado Segundo a NBR 6118:2014. São Carlos: EdUFSCar, 2014.
Gostaria de ter acesso a um curso sobre modelagem de alvenaria estrutural no Revit?
Aproveite enquanto está com um preço especial.

Boa noite, como obter o formulario-calculadora-flexao??!,
Olá, Roner,
Procura em materiais gratuitos no menu.
Abraço!
o que não aprendi na faculdade aprendi neste post parabenes
Luiz, bom dia!
Excelente tutorial. Pude rememorar as aulas do curso de engenharia civil em 1975.
Grato pelo apoio.
como obtenho a planilha para o cálculo de armadura dupla?
abraço.
Olá, Alberto,
A calculadora de flexão está temporariamente inativa. Assim que voltar colocarei nos materiais para download.