Entender os processos para o dimensionamento de seções submetidas à flexão pode ser bem desafiador. A boa notícia é que se você continuar nesse post irá aprender realmente o sentido das fórmulas que utiliza!
Nesse post você aprenderá as hipóteses de cálculo utilizada nas formulações de dimensionamento de seções submetidas à flexão.
Hipóteses básicas para o dimensionamento à flexão
Antes de passarmos para a dedução das formulações de dimensionamento, é necessário entendermos algumas hipóteses, presentes na ABNT/NBR: 6118 (2014), que são assumidas para essas deduções.
Seções planas
Admite-se que as seções que originalmente são planas permanecem planas após as deformações. Dessa forma, a deformação em cada ponto é proporcional a sua distância para a linha neutra.
Aderência entre concreto e aço
No dimensionamento à flexão é assumida uma total aderência entre o concreto e o aço. Logo, não é considerado nenhum escorregamento da armadura no concreto.
Assim, a deformação em qualquer ponto é obtida a partir da hipótese anterior, não importando se corresponder ao aço ou ao concreto.
Concreto tracionado
As tensões de tração no concreto, normais à seção transversal, não são consideradas no Estado Limite Último. Sendo assim, todo o esforço de tração é resistido unicamente pelas armaduras.
Considerações dos materiais para o dimensionamento
Diagrama tensão-deformação do concreto
O diagrama tensão-deformação idealizado para o concreto em compressão é fornecido na norma brasileira. Esse diagrama apresenta um patamar a partir da tensão \mathrm{0,85 \cdot f_{cd}}.
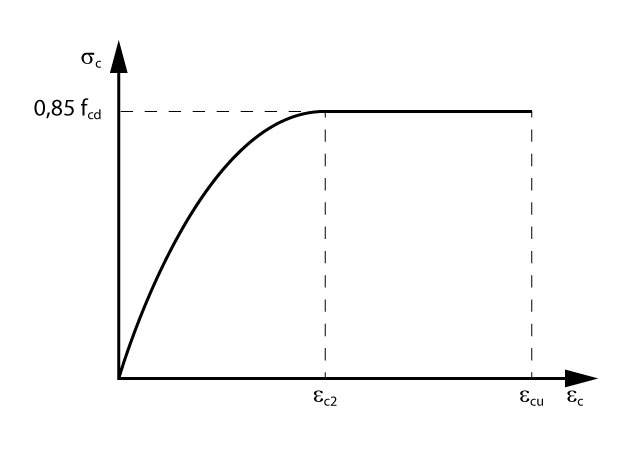
A região inicial curva é descrita pela equação abaixo:
\mathrm{\sigma_c=0,85 \cdot f_{cd} \cdot \left[ 1- \left(1- \dfrac{\epsilon_c}{\epsilon_{c2}} \right) ^n \right]}
O valor de \mathrm{n} irá variar com a classe do concreto utilizada. Para concretos de até 50 MPa, considera-se \mathrm{n=2}. Enquanto o valor de \mathrm{n} para concreto com resistência característica superior a 50 MPa vale:
\mathrm{n = 1,4+23,4 \cdot \left( \dfrac{90 - f_{ck}}{100} \right) ^4}
Para concretos até 50 MPa assume-se \mathrm{\epsilon_{c2} = 2,0 \; ‰} e \mathrm{\epsilon_{cu} = 3,5 \; ‰}. Enquanto para concretos de classes C55 até C90:
\mathrm{\epsilon_{c2} = 2,0 \; ‰ + 0,085 \; ‰ \cdot (f_{ck}-50) ^{0,53}}
\mathrm{\epsilon_{cu} = 2,6 \; ‰ + 35 \; ‰ \cdot \left( \dfrac{90 - f_{ck}}{100} \right) ^4}
Diagrama tensão-deformação do aço
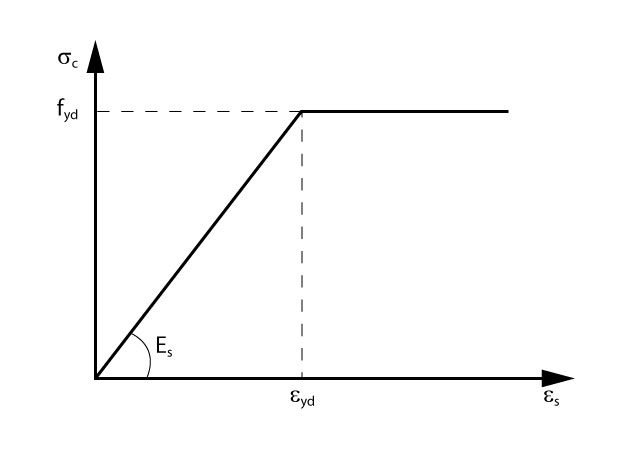
A norma ABNT/NBR: 6118 (2014) utiliza um diagrama tensão-deformacão simplificado para os aços de armadura passiva.
Distribuição de tensões na seção
As distribuições de tensões no concreto é realizada conforme a equação apresentada para o diagrama tensão-deformação, em que a tensão de compressão máxima vale \mathrm{0,85 \cdot f_{cd}}. Lembrando que, ao seguir essa equação, teremos uma parábola para deformações até \mathrm{\epsilon_{c2}} e um trecho reto a partir desta deformação até \mathrm{\epsilon_{cu}}.
A norma permite que, ao invés de utilizar um diagrama parábola-retângulo, consideremos um diagrama retangular simplificado. Este bloco retangular de tensões terá altura \mathrm{y=\lambda \cdot x}.
Onde \mathrm{x} indica a posição da linha neutra medida a partir da borda comprimida.
O valor de \mathrm{\lambda} irá variar com a classe do concreto utilizada. Para concretos de até 50 MPa, considera-se \mathrm{\lambda=0,8}. O valor de \mathrm{\lambda} para concreto com resistência característica superior a 50 MPa vale:
\mathrm{\lambda = 0,8 - \dfrac{f_{ck} - 50}{400}}
As tensões do bloco retangular valem \mathrm{\alpha_c \cdot f_{cd}} no caso da largura da seção, medida paralelamente à linha neutra, não diminuir a partir desta para a borda comprimida. Em contrapartida, caso a largura da seção diminua em direção a borda tracionada, as tensões valerão \mathrm{0,9 \cdot \alpha_c \cdot f_{cd}}.
O valor de \mathrm{\alpha_c} irá variar com a classe do concreto utilizada. Para concretos de até 50 MPa, considera-se \mathrm{\alpha_c=0,85}. O valor de \mathrm{\alpha_c} para concreto com resistência característica superior a 50 MPa vale:
\mathrm{\alpha_c = 0,85 \cdot \left( 1,0 - \dfrac{f_{ck}-50}{200} \right)}
A figura abaixo apresenta a simplificação do diagrama explicada acima. Na esquerda temos a distribuição linear das deformações, onde observa-se a posição \mathrm{x} da linha neutra e a posição em que a deformação vale \mathrm{\epsilon_{c2}}. Na figura intermediária, temos o diagrama parábola-retângulo, em que observamos o trecho reto após \mathrm{\epsilon_{c2}}. Por fim, na figura da direita, vemos a simplificação do diagrama parábola-retângulo em um diagrama retangular.

Domínios de deformação
Caso você prefira, pode acompanhar essa explicação de domínios a partir do vídeo abaixo:
A ruína de uma seção transversal é caracterizada pelo concreto ou o aço atingirem deformações específicas máximas estipuladas pela norma brasileira. Dessa forma, a ruína de uma seção pode ocorrer:
- deformação de alongamento na armadura atingir o valor de \mathrm{\epsilon_s=10,0 \; ‰};
- deformação de encurtamento no concreto em seções parcialmente comprimidas atingir a deformação \mathrm{\epsilon_{cu}} (\mathrm{\epsilon_{cu}=3,5 \; ‰} para concreto de classe até C50).
- deformação de encurtamento no concreto em seções inteiramente comprimidas atingir a deformação \mathrm{\epsilon_{c2}} (\mathrm{\epsilon_{cu}=2,0 \; ‰} para concreto de classe até C50).
Assim sendo, a norma brasileira fornece um conjunto de domínios que abarcam as possibilidades de ruptura à flexão de uma seção:
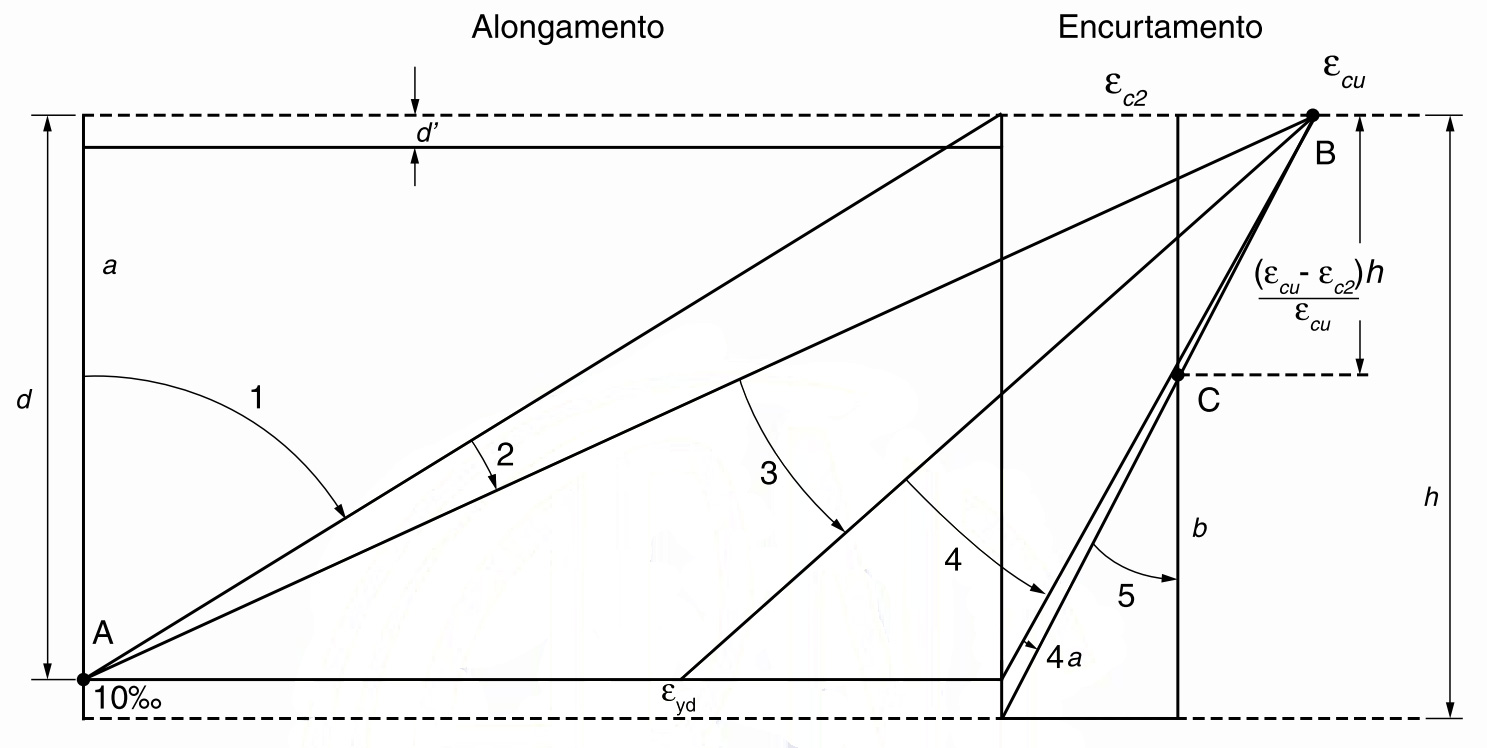
Domínio 1
- O Estado Limite Último é caracterizado pela deformação do aço \mathrm{\epsilon_s=10,0 \; ‰};
- A reta que representa a deformação gira em torno do ponto A (deformação do aço em 10,0 ‰), sendo que a deformação no concreto varia de 10,0 ‰ até 0;
- Esse domínio é caracterizado por tração simples (reta sobre o ponto A) ou tração não uniforme.
Domínio 2
- O Estado Limite Último é caracterizado pela deformação do aço \mathrm{\epsilon_s=10,0 \; ‰};
- A reta que representa a deformação continua girando em torno do ponto A (deformação do aço em 10,0 ‰), sendo que a deformação no concreto varia de 0 até \mathrm{\epsilon_{cu}=3,5 \; ‰};
- Nesse domínio a linha neutra irá variar de 0 até \mathrm{\dfrac{d \cdot \epsilon_{cu}}{0,01 + \epsilon_{cu}}};
- Esse domínio é caracterizado por flexão simples ou composta.
Domínio 3
- O Estado Limite Último é caracterizado pela deformação no concreto \mathrm{\epsilon_{cu}};
- A reta que representa a deformação agora gira em torno de \mathrm{\epsilon_{cu}}, sendo que a deformação no aço varia de 10,0 ‰ até \mathrm{\epsilon_{yd}};
- Nesse domínio a linha neutra irá variar de \mathrm{\dfrac{d \cdot \epsilon_{cu}}{0,01 + \epsilon_{cu}}} até \mathrm{\dfrac{d \cdot \epsilon_{cu}}{\epsilon_{yd} + \epsilon_{cu}}};
- Esse domínio é caracterizado por flexão simples ou composta.
Domínio 4
- No Estado Limite Último a seção rompe antes do aço escoar, de modo a ocorrer ruptura frágil;
- A reta que representa a deformação continua girando em torno de \mathrm{\epsilon_{cu}}, sendo que a deformação no aço varia de \mathrm{\epsilon_{yd}} ‰ até 0;
- Nesse domínio a linha neutra irá variar de \mathrm{\dfrac{d \cdot \epsilon_{cu}}{\epsilon_{yd} + \epsilon_{cu}}} até d;
- Esse domínio é caracterizado por flexão simples ou composta.
Domínio 4a
- No Estado Limite Último a seção rompe antes do aço escoar, de modo a ocorrer ruptura frágil;
- A reta que representa a deformação continua girando em torno de \mathrm{\epsilon_{cu}}, sendo que a deformação no aço varia de \mathrm{\epsilon_{yd}} ‰ até 0;
- Esse domínio é caracterizado por flexão composta com armaduras comprimidas.
Domínio 5
- O Estado Limite Último é caracterizado pela deformação no concreto de \mathrm{\epsilon_{cu}} para flexocompressão ou \mathrm{\epsilon_{c2}} para compressão uniforme;
- A reta que representa a deformação agora gira em torno do ponto C;
- Esse domínio é caracterizado por compressão não uniforme.
Dessa maneira, para seções submetidas à flexão simples a ruptura pode ocorrer nos domínios 2, 3 e 4, seções submetidas a flexo-tração, podem ocorrer os domínios 1, 2, 3 e 4 e seções submetidas a flexo-compressão, podem ocorrer os domínios 2, 3, 4, 4a e 5.
Limitações na posição da linha neutra
A norma brasileira limita a posição da linha neutra a fim de garantir boa condição de ductilidade.
\mathrm{x/d \leq 0,45}, para concretos até 50 MPa
\mathrm{x/d \leq 0,35}, para concretos de 50 MPa a 90 MPa
Caso seja aplicada alguma redistribuição de momento, significando assim alteração na rigidez viga-pilar, o novo limite da posição da linha neutra é dado em relação ao momento reduzido \mathrm{\delta \cdot M}:
\mathrm{x/d \leq \dfrac{\delta - 0,44}{1,25}}, para concretos até 50 MPa
\mathrm{x/d \leq \dfrac{\delta - 0,56}{1,25}}, para concretos de 50 MPa a 90 MPa
Nesse post você aprendeu a base para o dimensionamento de seções submetidas flexão. Se você gostou desse texto ou se ainda possui alguma dúvida, deixe uma mensagem nos comentários abaixo!
Fonte:
ARAÚJO, J. M. Curso de Concreto Armado. Rio Grande: Editora Dunas, 2014. v. 1
ASSOCIAÇÃO BRASILEIRA DE NORMAS TÉCNICAS. NBR 6118: Projeto de estruturas de concreto – Procedimento. Rio de Janeiro, 2014.
CARVALHO, R. C.; FIGUEIREDO FILHO, J. R. Cálculo e Detalhamento de Estruturas Usuais de Concreto Armado Segundo a NBR 6118:2014. São Carlos: EdUFSCar, 2014.
Gostaria de ter acesso a um curso sobre modelagem de alvenaria estrutural no Revit?
Aproveite enquanto está com um preço especial.
