Visto que você já sabe como calcular a área de aço longitudinal necessária para vigas de concreto submetidas a flexão simples e também a área de aço dos estribos, o próximo passo será entrarmos no detalhamento de vigas em si. Nós realizaremos aqui o detalhamento da seção transversal de uma viga de concreto armado.
Sendo assim, aqui você irá aprender os seguintes tópicos relativos ao detalhamento da seção transversal:
- Cobrimento nominal;
- Espaçamento mínimo entre barras longitudinais;
- Armadura longitudinal máxima e mínima;
- Armadura de pele;
- Porta estribos.
Cobrimento nominal
Primeiramente, vamos começar pela definição do cobrimento nominal, cuja função é garantir a durabilidade do elemento estrutural.
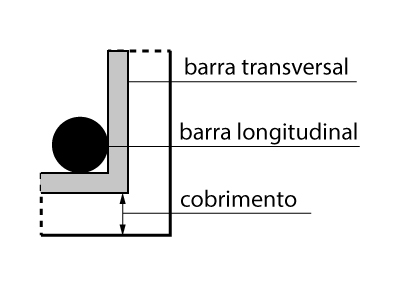
O cobrimento nominal pode ser obtido, em função da classe de agressividade ambiental (CAA) e da peça que estamos analisando. Uma vez que, esse post estamos tratando apenas do detalhamento de vigas, a tabela abaixo nos informa o cobrimento que devemos utilizar.

Espaçamento mínimo entre barras longitudinais no detalhamento
Da mesma forma, outro ponto que devemos nos atentar ao detalhar uma seção transversal de uma viga é o espaçamento mínimo entre as barras longitudinais. Na imagem abaixo, são apresentados os espaçamentos horizontais e verticais mínimos.
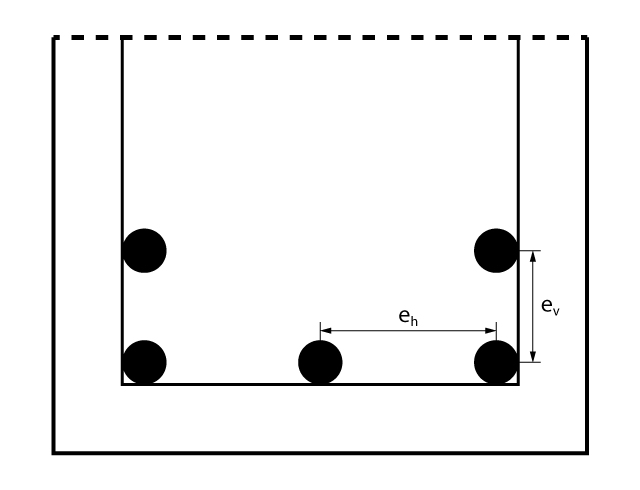
De acordo com a ABNT/NBR: 6118 (2014), o espaçamento horizontal mínimo vale:
\mathrm { e_h = \left\{ \begin{array}{ll} 20 \; mm \\ \phi_l \\ 1,2 \cdot \phi_{ag} \end{array} \right. }
Em que \mathrm {\phi_l} vale o diâmetro da barra longitudinal e \mathrm {\phi_{ag}} vale o diâmetro máximo do agregado.
Conhecendo o valor de \mathrm{e_h}, podemos calcular o espaço necessário (na região interna do estribo), para alojar uma quantidade \mathrm{n} de barras em uma camada.
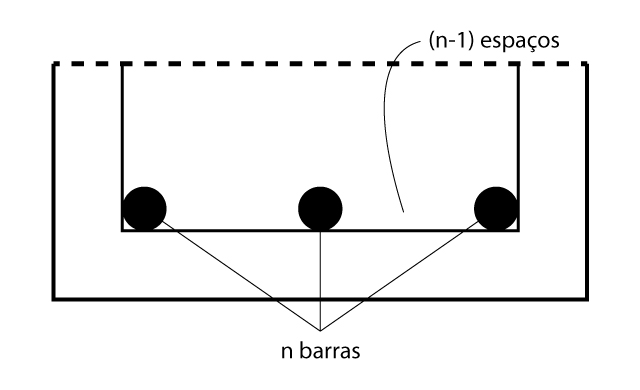
\mathrm{b_{nec} = n \cdot \phi + \left( n-1 \right) \cdot e_h}
Assim sendo, a largura necessária \mathrm{b_{nec}} deve ser superior a largura disponível \mathrm{b_{disp}}, que é obtida da dedução do cobrimento e do diâmetro do estribo na largura da viga:
\mathrm{b_{disp} = b_w - 2 \cdot \phi_t - 2 \cdot C}
Em seguida, vamos para o espaçamento vertical entre as barras:
\mathrm { e_v = \left\{ \begin{array}{ll} 20 \; mm \\ \phi_l \\ 0,5 \cdot \phi_{ag} \end{array} \right. }
Armaduras longitudinais mínimas e máximas
A armadura longitudinal mínima deve ser dada pelo dimensionamento da seção para um momento fletor mínimo, devendo-se respeitar a taxa de aço mínima de 0,15%.
\mathrm{M_{d,mín}=0,8 \cdot W_0 \cdot f_{ctk,sup}}
Onde \mathrm{W_0} é o módulo da seção de concreto, relativo à fibra mais tracionada e \mathrm{f_{ctk,sup}} é a resistência característica superior do concreto à tração.
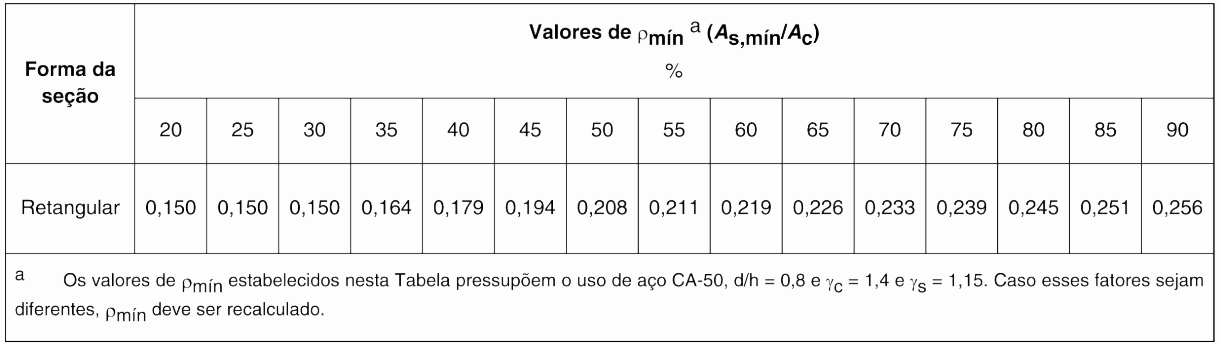
Com o intuito de encontrarmos a taxa mínima de armadura de maneira mais direta, a norma brasileira nos fornece a tabela abaixo.
Analogamente ao desenvolvido para armadura mínima, a área de aço máxima também é uma porcentagem da seção bruta de concreto. Sendo assim, o somatório da armadura tracionada com a armadura comprimida, fora da zona de emenda, deve ser no máximo de 4% da área de concreto.
Detalhamento da armadura de pele
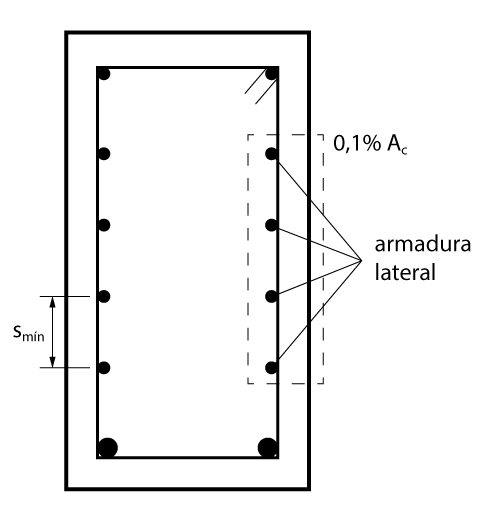
Para vigas altas, a fim de limitar as fissuras, é necessário adicionar armaduras de pele (também denominadas de armaduras laterais ou costelas) em cada face da viga. A norma brasileira demanda a utilização para vigas com altura superior a 60 cm.
A norma recomenda o valor mínimo de \mathrm{0,1 \% \cdot b_w \cdot h} por face, não sendo necessário uma armadura superior a 5 cm²/m.
Além disso, também devemos respeitar o espaçamento mínimo fornecido pela formulação abaixo.
\mathrm { s_{min} = \left\{ \begin{array}{ll} d/3 \\ 20 \; cm \\ 15 \cdot \phi \end{array} \right. }
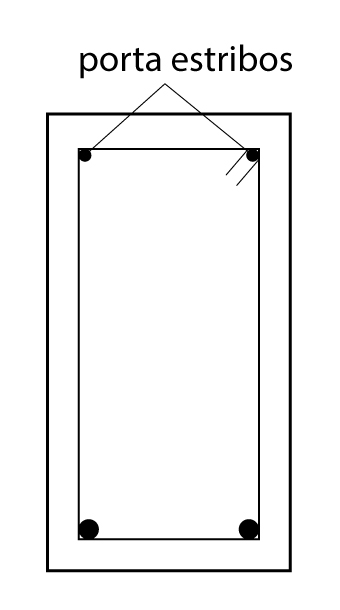
Porta estribos
No caso de não existir armadura comprimida, devem ser inseridas armaduras, denominadas de porta estribos com diâmetro pelo menos igual ao do estribo. Essas armaduras tem função apenas construtiva.
A imagem abaixo apresenta o detalhamento de uma viga com a utilização da armadura construtiva denominada de porta estribo.
Exemplo aplicado de detalhamento de vigas
A fim de aplicarmos os conceitos estudados até então, vamos detalhar a seção transversal de uma viga de dimensões 14 cm x 40 cm, com concreto classe C20, já dimensionada anteriormente para uma área de aço longitudinal de 1,9 cm².
Caso você prefira, você pode acompanhar a resolução a partir do vídeo abaixo!
Limites de armadura
Vamos primeiramente calcular os limites mínimos e máximos para a armadura. De acordo com a tabela apresentada anteriormente, para um concreto de 20 MPa, devemos considerar uma taxa de armadura mínima \mathrm{\rho_{min}=0,15 \; \%}. Logo:
\mathrm{A_{s,min}=\dfrac{0,15}{100} \cdot 14 \cdot 40 = 0,84 \; cm^2}
Em segundo lugar, vamos verificar a armadura máxima. Para isso, iremos considerar 4% da área de concreto:
\mathrm{A_{s,max}=\dfrac{4}{100} \cdot 14 \cdot 40 = 22,4 \; cm^2}
Iremos utilizar a área de aço de 1,9 cm², visto que a mesma encontra-se dentro dos limites calculado acima.
Caso eventualmente encontrarmos uma área de aço inferior a armadura mínima, devemos seguir o detalhamento utilizando a armadura mínima encontrada. Já para a situação de uma área de aço calculada superior a área de aço máxima, a recomendação inicial é aumentar a altura da viga.
Armadura de pele
Posto que, a altura da viga é inferior a 60 cm, é possível dispensar o uso de armadura lateral. Dessa forma, assim o faremos.
Espaçamento das armaduras
A princípio, vamos calcular a largura disponível para colocar as armaduras longitudinais. Lembrando que o cobrimento utilizado foi 2,5 cm e considerando uma armadura transversal de 5 mm, teremos:
\mathrm{b_{disp}=140 - 2 \cdot 25 - 2 \cdot 5=80 \; mm}
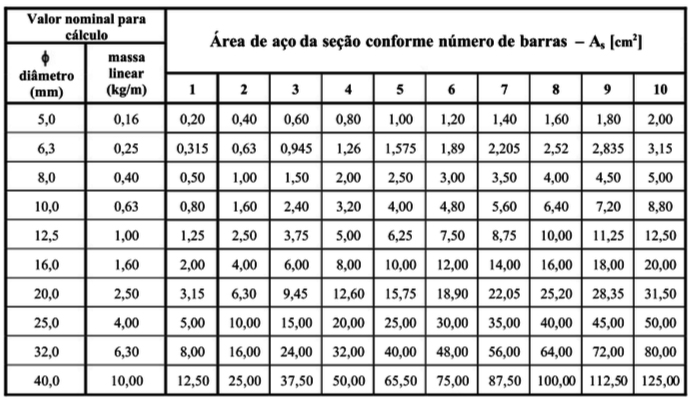
Em posse de uma tabela de área de aço por quantidade de barras, vamos considerar algumas situações de bitola:
- 12,5 mm;
- 10,0 mm;
- 8,0 mm.
Para o cálculo do espaçamento horizontal, vamos considerar uma diâmetro máximo do agregado de 19 mm. Dessa forma, independente das três bitolas escolhidas, o espaçamento será ditado pelo diâmetro máximo do agregado.
\mathrm { e_h = \left\{ \begin{array}{ll} 20 \; mm \\ \phi_l \\ 1,2 \cdot \phi_{ag} \end{array} \right. }
\mathrm { e_h = \left\{ \begin{array}{ll} 20 \; mm \\ \phi_l \\ 1,2 \cdot 19 = 22,8 \; mm \end{array} \right. }
\mathrm { e_h =22,8 \; mm}
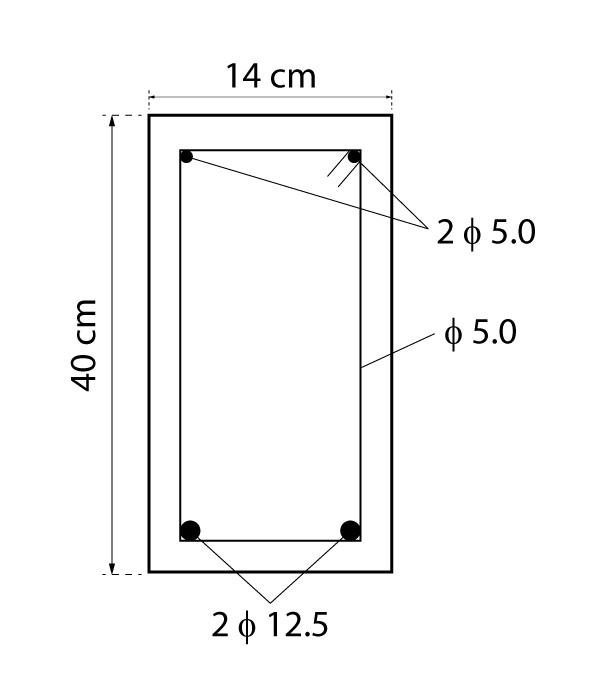
Situação 1: Bitola de 12,5 mm
De acordo com a tabela acima, serão necessárias duas barras de 12,5 mm para atendar a área de 1,9 cm². Calcula-se agora o o espaçamento necessário para alocar a armadura:
\mathrm{b_{nec} = n \cdot \phi + \left( n-1 \right) \cdot e_h}
\mathrm{b_{nec} = 2 \cdot 12,5 + \left( 2-1 \right) \cdot 22,8 = 47,8 \; mm}
Como \mathrm{b_{nec} \leq b_{disp}}, podemos utilizar apenas uma camada de armadura.
Situação 2: Bitola de 10,0 mm
Ainda de acordo com a tabela acima, serão necessárias três barras de 10,0 mm para atendar a área de 1,9 cm². É calculado então o \mathrm{b_{nec}} para alocar a armadura:
\mathrm{b_{nec} = n \cdot \phi + \left( n-1 \right) \cdot e_h}
\mathrm{b_{nec} = 3 \cdot 10,0 + \left( 3-1 \right) \cdot 22,8 = 75,6 \; mm}
Como \mathrm{b_{nec} \leq b_{disp}}, podemos utilizar apenas uma camada de armadura.
Situação 3: Bitola de 8,0 mm
Da mesma forma para barras de 8,0 mm, serão necessárias quatro barras para atendar a área de 1,9 cm². Calcula-se posteriormente o espaçamento necessário para alocar a armadura:
\mathrm{b_{nec} = n \cdot \phi + \left( n-1 \right) \cdot e_h}
\mathrm{b_{nec} = 4 \cdot 8,0 + \left( 4-1 \right) \cdot 22,8 = 100,4 \; mm}
Como \mathrm{b_{nec} > b_{disp}}, será necessário utilizar duas camadas de armadura. Podendo dispor assim, duas barras por camada.
Porta estribos
Uma vez que, estamos utilizando um estribo de 5,0 mm, vamos utilizar a mesma bitola como armadura construtiva. Dessa forma, para essa seção, utilizaremos duas barras de 5,0 mm na região superior da viga.
Detalhamento final
A figura abaixo apresenta o detalhamento final para a seção transversal utilizada no exemplo.
Recado final
Em suma, o objetivo dessa publicação é fornecer a você conhecimentos práticos sobre o detalhamento de vigas de concreto armado submetidas flexão simples, focando apenas na sua seção transversal
Se você tem interesse em ingressar na área de cálculo estrutural, recomendo bastante o curso Essencial em Concreto Armado do professor Rangel Lage em que você irá aprender a utilizar o software TQS (na minha opinião, o melhor software do mercado) passando por TODAS as etapas (desde a concepção estrutural até elaboração das pranchas) necessárias para o desenvolvimento de um projeto completo.
Fonte:
ARAÚJO, J. M. Curso de Concreto Armado. Rio Grande: Editora Dunas, 2014. v. 1
ASSOCIAÇÃO BRASILEIRA DE NORMAS TÉCNICAS. NBR 6118: Projeto de estruturas de concreto – Procedimento. Rio de Janeiro, 2014.
CARVALHO, R. C.; FIGUEIREDO FILHO, J. R. Cálculo e Detalhamento de Estruturas Usuais de Concreto Armado Segundo a NBR 6118:2014. São Carlos: EdUFSCar, 2014.
Gostaria de ter acesso a um curso sobre modelagem de alvenaria estrutural no Revit?
Aproveite enquanto está com um preço especial.

Parabéns , gostei do artigo. Sugiro você escrever sobre dimensionamento de blocos de ancoragem de tubulações (enterrados e aéreos )
Valeu pelo comentário, Ilka!
Muito obrigado pela sugestão, iremos adicionar ela na lista de posts futuros.
Até a próxima,
Abraços!
Gostei bastante do conteúdo!
Muito obrigado, July!
Parabéns …, gostei do vosso do vosso conteúdo, é excelente.
Obrigado pelo retorno, Fernando.
Abraços!
Excelente trabalho. Muito simples e didático.
Muito obrigado pelo comentário, Marco.
Fico feliz que tenha lhe sido útil.
Abraços!
Gostei, muito boa explicação.Deveria colocar mais um exemplo, de cálculo de armadura de viga mais alta, necessitando de armadura de pele.
Olá, Lacerda,
Obrigado pelo comentário.
Dá uma conferida no vídeo no YouTube que acho que no exemplo lá eu coloco.
Abraços!
excelente explicação
Obrigado, Mário!