Você quer aprender a calcular o recalque de fundações em solos arenosos? Então você está no lugar certo! Nesse post você verá o método de Schmertmann para a estimativa de recalque em areias!
Lembrando que caso você tenha caído de pára-quedas nesse post, recomendo também que você leia nossos posts anteriores sobre os conceitos iniciais de recalque e estimativa de recalque em meios elásticos homogêneos.
Além de complementar seu aprendizado, ambos os textos também servirão para um embasamento teórico maior para acompanhar esse post.
Então, vamos agora ao conteúdo!
Recalques em areia
As areias não podem ser consideradas como meios elásticos homogêneos. O que isso quer dizer?
Que, mesmo para areias com granulometria homogênea, seu módulo de deformabilidade não é constante independente da profundidade.
Ou seja, o módulo de deformabilidade do solo (\mathrm{E_s}) aumenta com o aumento da profundidade, devido ao efeito de confinamento nesse tipo de solo.
Então, como podemos estimar o recalque para solos arenosos?
Bem, o que podemos fazer é dividir o solo em várias camadas de pequenas espessuras, de forma a considerar que para tal camada, teremos um \mathrm{E_s} constante. Então, podemos resolver como um problema de multicamadas para MEH.
Com base nessa consideração, e também através da utilização da Teoria da Elasticidade, Schmertamann elaborou em 1970 um método para a estimativa de recalque em areias. Tal método foi aprimorado em 1978. A seguir, veremos cada um com mais calma!
Lembrando que, caso você queira aprender mais sobre esse conteúdo, eu indico o livro do Prof. Cintra e Prof. Albiero, Fundações Diretas. Projeto Geotécnico. É um livro que possui uma leitura simples, bem didática, mas com muito conteúdo teórico. É um ótimo livro para ingressar na área de Geotecnia!
Método de Schmertmann (1970)
Schmertmann, através da fundamentos teóricos e de modelos computacionais, estudou a deformação vertical em solos arenosos submetidos à carregamentos externos. Então, chegou à seguinte formulação:
\mathrm{\varepsilon_z=\dfrac{\sigma}{E_s}\cdot I_z}
Onde:
- \mathrm{\varepsilon_z}: deformação vertical na profundidade z;
- \mathrm{\sigma}: carregamento uniforme;
- \mathrm{I_z}: fator de influência na deformação, obtido por meio do gráfico abaixo.

Podemos perceber, por esse gráfico de \mathrm{I_z} que a máxima deformação não ocorre na superfície de contato entre a fundação e o solo, porém, a uma profundidade \mathrm{z=B/2}, em que B é a largura da fundação.
Percebemos também que, a partir dessa profundidade, as deformações vão se tornando menores, até terem valores mínimos a uma profundidade \mathrm{z=2B}.
Para complementar a formulação anterior, podemos considerar o embutimento da fundação, que vai minorar as deformações obtidas. Podemos também estimar a deformação ao longo do tempo. Para isso, vamos utilizar os coeficientes C1 e C2, respectivamente.
Embutimento da fundação
Para considerar o embutimento da fundação no cálculo de recalque por meio do Método de Schmertmann, utilizaremos o coeficiente C1, que pode ser determinado através da seguinte formulação:
\mathrm{C_1=1-0,5\cdot\dfrac{q}{\sigma^*}\geq 0,5}
Onde:
- \mathrm{q}: tensão vertical efetiva na cota de apoio da fundação;
- \mathrm{\sigma*}: tensão líquida aplicada pela fundação (\mathrm{\sigma*=\sigma-q})
Entenda que utilizamos a tensão líquida visto que a parcela de sobrecarga q, teoricamente não deve gerar recalque no solo, já que houve um alívio de tensões com esse valor decorrente da escavação do solo para execução da fundação.
Em fundações rasas, a consideração da tensão líquida não apresenta grande influência no recalque, porém, em fundações profundas, como tubulões, a utilização do coeficiente de embutimento gera valores consideráveis na redução do recalque.
Efeito do tempo
Embora estudos comprovem que em solos arenosos o recalque imediato seja responsável pela grande parcela do recalque total do solo, nós também podemos estimar o recalque ao longo do tempo, através do coeficiente de correção C2, dado na fórmula abaixo:
\mathrm{C_2=1+0,2\cdot log\left(\dfrac{t}{0,1}\right)}
Onde:
- t: tempo em anos.
Caso você queira ignorar o recalque ao longo do tempo e considerar apenas o recalque imediato, basta considerar \mathrm{C_2=1}.
Formulação
Então, para finalizar o conteúdo referente ao método de Schmertmann de 1970, vamos apresentar a formulação final, que nada mais é do que a fórmula apresentada inicialmente acrescida dos coeficientes de correção C1 e C2, conforme apresentado abaixo:
\mathrm{\displaystyle\rho_d=C_1\cdot C_2\cdot\sigma^*\cdot \sum_{i=1}^{n} \left(\dfrac{I_z}{E_s}\cdot \Delta_z \right)_i}
Onde:
- \mathrm{\displaystyle\rho_d}: recalque total;
- \mathrm{\displaystyle {I_z}}: fator de influência à meia altura da i-nésima camada;
- \mathrm{\displaystyle {E_s}}: módulo de deformabilidade da i-nésima camada;
- \mathrm{\displaystyle\Delta_z}: espessura da i-nésima camada;
Lembrando que, para a estimativa do módulo de deformabilidade podemos usar a formulação simples de Teixeira e Godoy, que associam tal parâmetro com o índice Nspt do solo. A formulação é a seguinte:
\mathrm{E_s=\alpha\cdot K \cdot Nspt}
Onde \mathrm{\alpha} e K variam de acordo com o solo e podem ser obtidos através das tabelas abaixo.
|
Solo |
\mathrm{\alpha} |
|
Areia |
3 |
|
Silte |
5 |
|
Argila |
7 |
|
Solo |
K (Mpa) |
| Areia com pedregulhos |
1,1 |
|
Areia |
0,9 |
|
Areia siltosa |
0,70 |
|
Areia argilosa |
0,55 |
|
Silte arenoso |
0,45 |
|
Silte |
0,35 |
|
Argila arenosa |
0,30 |
|
Silte argiloso |
0,25 |
|
Argila siltosa |
0,20 |
Roteiro de cálculo
Agora, para enfim, utilizarmos corretamente o método de Schmertmann, vamos seguir os cinco passos a seguir:
- Calcular valores de q, \mathrm{\sigma^*}, C1 e C2 (lembrando que o valor de C2 é opcional, caso você queira determinar o recalque ao longo do tempo);
- Desenhar o triângulo do fator de influência \mathrm{I_z} a partir da base da fundação;
- Dividir o solo abaixo da fundação em subcamadas com valores de Es constantes e espessura máxima B/2, de forma nessa divisão, alguma subcamada coincida com a profundidade B/2 (valor máximo de Iz para o triângulo criado no passo 2);
- Fazer uma tabela com seis colunas: número da camada, \mathrm{\Delta_z},Iz, Nspt, Es e \mathrm{I_z\Delta_z/E_s};
- Fazer o somatório dos valores da última coluna e multiplicá-lo por C1, C2 e \mathrm{\sigma^*}.
Pronto! Sei que pode parecer difícil, mas não se preocupe, se ainda ficou alguma dúvida, tenho certeza que no próximo post, com uma questão resolvida você entenderá tudo!
Agora vamos estudar um pouco sobre o método aprimorado de Schmertmann, de 1978.
Método de Schmertmann (1978)
O método de Schmertmann de 1978 é um aprimoramento da metodologia anterior. Não há muitas modificações, mas substitui o método de 1970.
As principais diferenças do método de Schmertmann de 1978 para o de 1970 são que o novo faz uma diferenciação entre sapatas quadradas e sapatas corridas e, consequentemente, apresenta um novo gráfico para determinação de Iz, apresentado abaixo:
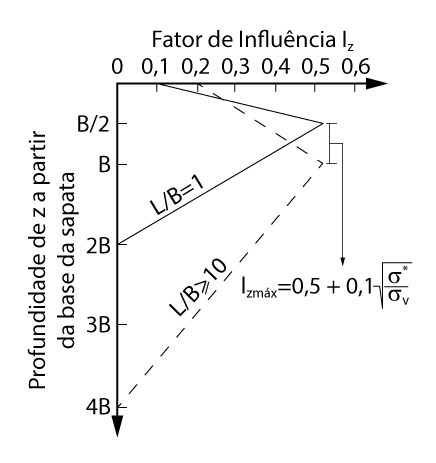
Podemos perceber algumas mudanças nesse novo gráfico, em comparação com o anterior. Percebemos que o valor de \mathrm{I_{zmáx}} não é mais constante e agora varia segundo a seguinte formulação:
\mathrm{I_{zmáx}=0,5+0,1\cdot\sqrt{\dfrac{\sigma^*}{\sigma_v}}}
Onde:
- \mathrm{{\sigma_v}}: tensão vertical efetiva na profundidade correspondente a \mathrm{I_{zmáx}}.
Para fundações que nem sejam quadradas, mas também não atendam a condição de \mathrm{L/B\geq 10}, devemos construir um diagrama intermediário entre os dois já apresentados pelo gráfico de Schmertmann, de forma que o “bulbo de recalque”, ou seja, a ordenada máxima do gráfico seja:
\mathrm{z=2B\cdot[1+log(L/B)]}
Vale ressaltar também que, apesar de o método ser desenvolvido para fundações, pode também ser utilizado para a estimativa de recalque em tubulões, visto que há um fator de correção (C1) para o embutimento da fundação no solo.
E isso é tudo pessoal!
Caso você queira saber um pouco mais sobre o assunto, leia nosso post com um exercício resolvido pelo método de Schmertmann.
Espero que você tenha gostado! Se ainda ficou alguma dúvida, deixa nos comentários que a gente te responde.
Não deixe de seguir nosso blog, assinar nossa newsletter, além de acompanhar nosso canal no Youtube e ficar por dentro das novidades!
Até a próxima!
Engenheiro Civil, Especialista em Estruturas e Fundações. Ex-goleiro, Pseudosommelier de Cervejas e Poeta Freelancer Fajuto.
