Cálculo do recalque no solo: meios elásticos homogêneos

Se você leu nosso post anterior sobre os conceitos iniciais de recalque, deve ter ficado se perguntando: como eu posso calcular os recalques da minha fundação?

Então eu te respondo: nesse post você vai aprender métodos para estimar o recalque de fundações assentes em solos de meio elásticos homogêneos!

Ficou confuso? Fica tranquilo, prometo que no fim da leitura você estará entendendo tudo!

Vamos lá?

Recalque e o módulo de deformabilidade

Antes de iniciarmos o conteúdo propriamente dito, vamos só relembrar um pequeno detalhe do post anterior:

Nós podemos dividir o recalque absoluto (\mathrm{\rho}) em duas parcelas:

\mathrm{\rho=\rho_c+\rho_i}

Onde:

• \mathrm{\rho_c}: recalque por adensamento;
• \mathrm{\rho_i}: recalque imediato;

Embora o recalque por adensamento não possa ser ignorado em solos argilosos saturados, pois pode apresentar valores elevados, nesse post nos reteremos mais ao estudo do cálculo do recalque imediato!

É muito importante entender a relação entre o cálculo do recalque imediato e o módulo de deformabilidade do solo, visto que tal cálculo é feito a partir da Teoria da Elasticidade.

Mas afinal, o que é módulo de deformabilidade?

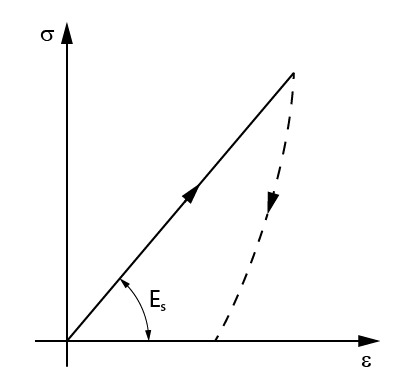
Sabe aquele nosso velho gráfico conhecido de tensão x deformação? Pois é, talvez você já tenha ouvido falar sobre módulo de elasticidade, que é a relação entre a tensão e a deformação, obtida através desse gráfico.

Módulo de deformabilidade tem exatamente o mesmo conceito!

Entretanto, como solos geralmente não apresentam característica elástica, ou seja, apresentam deformações permanentes quando submetidos a tensão normal, costuma-se chamar a relação entre tensão e deformação de módulo de deformabilidade (\mathrm{E_s})!

Então, podemos considerar para os solos um gráfico de tensão x deformação linear não elástico. Ou seja, apresenta linearidade entre tensão aplicada e deformação sofrida, porém, ao ser retirada a tensão, sofre deformações residuais. Podemos observar tal comportamento na figura abaixo.

De acordo com a variação de \mathrm{E_s} em função da profundidade do maciço de solo, podemos dividir tal maciço em três tipos:

• Meio elástico homogêneo (MEH): quando \mathrm{E_s} não varia em função da profundidade do solo;
• Meio elástico não homogêneo: quado \mathrm{E_s} varia em função da profundidade;
• Meio de Gibson: é um tipo específico de meio elástico não homogêneo. Nesse meio, \mathrm{E_s} é considerado zero na superfície e considera-se que ele varia linearmente com a profundidade.

Nesse post, trataremos da estimativa de recalques para MEH, que são representados principalmente por argilas sobreadensadas. Em um post futuro, falaremos de recalques em meios elásticos não homogêneos.

Camada semi-infinita

Vamos iniciar nosso estudo sobre recalque em MEH por uma situação simples: uma camada semi-infinita de solo.

Para essa situação, podemos utilizar a seguinte formulação:

\mathrm{\rho_i=\sigma\cdot B\cdot\dfrac{1-\nu^2}{E_s}\cdot I_p}

Onde:

• \mathrm{\sigma}: tensão média na superfície de contato entre fundação e solo;
• B: largura da fundação;
• \mathrm{\nu}: coeficiente de Poisson do maciço de solo;
• \mathrm{I_p}: fator de influência, que varia de acordo com a rigidez e forma da fundação, cujos valores são apresentados abaixo.

Ou seja, podemos perceber que em um MEH, sapatas flexíveis apresentam maiores recalques no centro e menores nas bordas.

Camada Finita

Nós já vimos a formulação para estimar o recalque imediato em camadas semi-infinitas.

Entretanto, muitas vezes existe apenas uma camada de “pequena espessura” sobre um material praticamente indeformável, como por exemplo, um maciço rochoso.

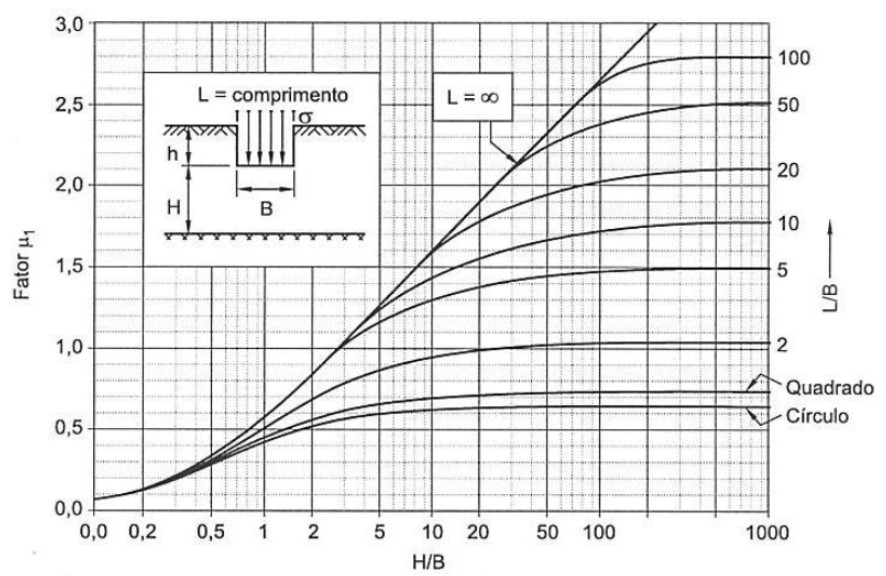
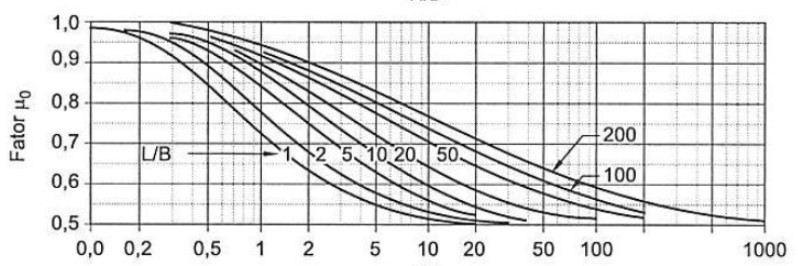
Nesse caso, podemos utilizar a solução de Janbu. Através da Teoria da Elasticidade e de considerações feitas, como \mathrm{\nu=0,5}, Janbu chegou a seguinte formulação para sapatas flexíveis:

\mathrm{\rho_i=\mu_0\cdot \mu_1\cdot\dfrac{\sigma\cdot B}{E_s}}

Onde:

• \mathrm{\mu_0} e \mathrm{\mu_1}: fatores de influência de embutimento da sapata e de espessura da camada de solo;

Considerando uma fundação de dimensões de base BxL ou uma circular de diâmetro B assentada a uma profundidade h e sendo H a distância da base da fundação ao maciço indeslocável, temos os seguintes ábacos para determinação de \mathrm{\mu_0} e \mathrm{\mu_1}

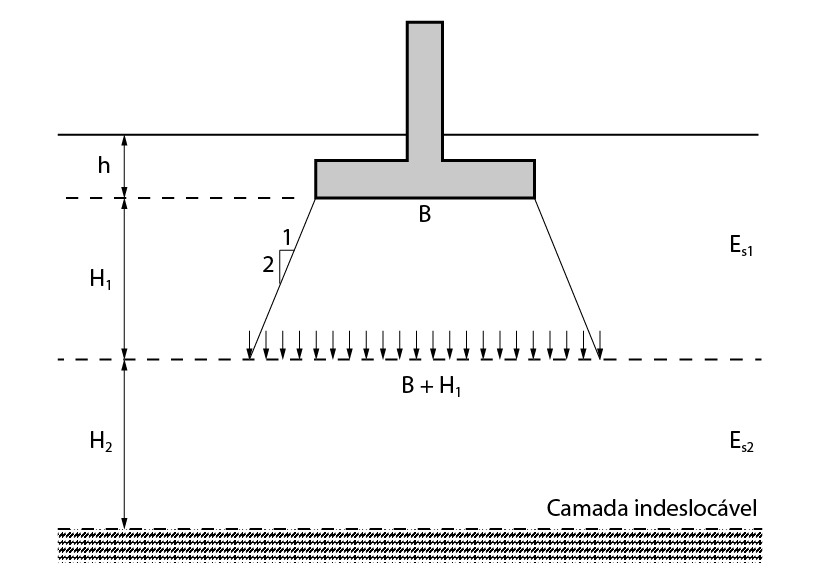
Multicamadas

Outra situação também bem usual é a ocorrência de diversas camadas de solo do tipo MEH, cada camada com seu módulo de deformabilidade definido, sobrejacentes a uma camada indeslocável, como apresentado na figura abaixo.

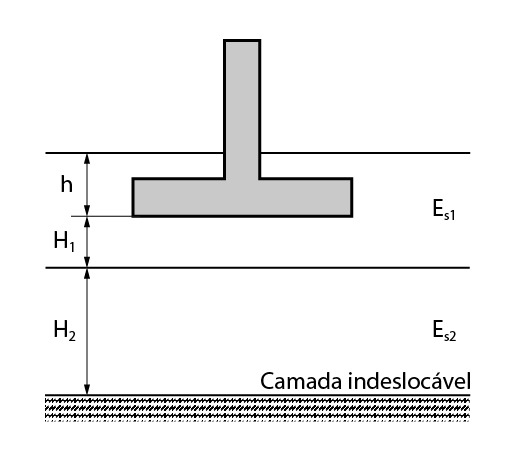
Nesse caso, podemos calcular o recalque do solo como sendo a soma dos recalques da camada 1 e da camada 2.

\mathrm{\rho_i=\rho_1+\rho_2}

Para o cálculo de \mathrm{\rho_1}, devemos considerar a camada 1 como uma camada finita. Além disso, a interface entre a primeira e a segunda camada deve ser considerada como a camada indeslocável.

Para o cálculo de \mathrm{\rho_2} devemos fazer as mesmas considerações de camada finita. Porém, além disso, devemos também fazer um pequeno ajuste nas dimensões da sapata, a fim de utilizarmos os ábacos de Janbu, e na tensão do solo no topo da camada 2, visto que há um espraiamento da carga da cota de assentamento inicial da sapata até a interface das camadas 1 e 2.

Ou seja, o que devemos fazer é considerar um espraiamento de carga na inclinação 1:2 da cota de assentamento até o topo da camada 2. As dimensões, bem como as tensões, calculadas a partir desse espraiamento é que deverão ser utilizadas para o cálculo de \mathrm{\rho_2}.

Entendeu tudo?

Caso tenha ficado algum dúvida, não se preocupe que em breve faremos um post com um exemplo resolvido para ficar ainda mais fácil pra você!

Parâmetros de compressibilidade

Se você chegou até aqui, pode estar se perguntando: tudo bem, eu até entendi tudo, mas como eu determino o módulo de deformabilidade das camadas e seus coeficientes de Poisson para aplicar as fórmulas apresentadas?

Então, vamos começar pelo módulo de deformabilidade.

Para a estimativa do módulo de deformabilidade podemos usar a formulação simples de Teixeira e Godoy, que associam tal parâmetro com o índice Nspt do solo. A formulação é a seguinte:

\mathrm{E_s=\alpha\cdot K \cdot Nspt}

Onde \mathrm{\alpha} e K variam de acordo com o solo e podem ser obtidos através das tabelas abaixo.

Para a estimativa do coeficiente de Poisson, podemos usar a tabela de Teixeira e Godoy apresentada abaixo.

Pronto! Viu como o cálculo de recalque no solo não é nenhum bicho-de-sete-cabeças? No próximo post você aprenderá a calcular os recalques para meios não homogêneos, como é o caso, geralmente, de areias.

Além disso, faremos ainda um post com problemas resolvidos para você aprender a aplicação das fórmulas apresentadas em ambos os posts!

Caso você tenha alguma dúvida ou tenha sugestões para temas futuros, deixa nos comentários que a gente responde!

Não deixe de seguir nosso blog, assinar nossa newsletter, além de acompanhar nosso canal no Youtube e ficar por dentro das novidades!

Até a próxima!

Filipe Marinho

Engenheiro Civil, Especialista em Estruturas e Fundações. Ex-goleiro, Pseudosommelier de Cervejas e Poeta Freelancer Fajuto.