Nesse post resolveremos juntos dois exercícios de estimativa de recalque em solos argilosos.
Vamos nos ater inicialmente a resolução de questões referentes à recalques em meios elásticos homogêneos (MEH), geralmente representado por solos argilosos sobreadensados.
Caso você ainda não tenha conferido nossos posts sobre a teoria de recalque e sobre os métodos para a determinação desse recalque, aconselho que dê uma olhada!
Agora, sem mais delongas, vamos para o post!
Exercício 1 – Recalque em camadas semi-infinitas
Vamos começar com um exercício bem simples!
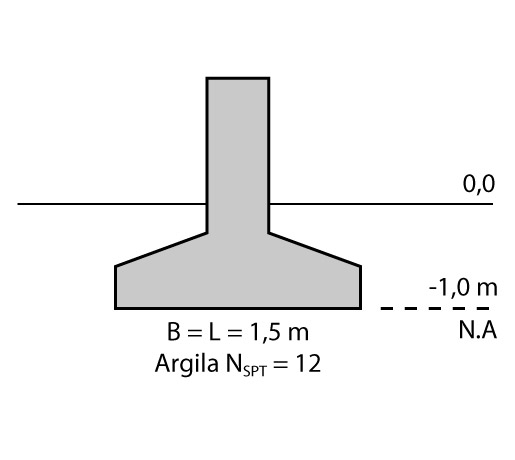
Considere uma sapata rígida de 1,50m x 1,50m de base, assentada a uma profundidade de 1,0m sobre uma camada de argila saturada sobreadensada que pode ser considerada como semi-infinita. Sabendo que a mesma recebe da superestrutura uma carga de 300 kN e que a Nspt dessa camada é igual a 12, estime o recalque imediato previsto para essa sapata.
Resolução
Bem, como o problema se trata de uma camada semi-infinita de argila sobreadensada e com o Nspt constante ao longo de sua profundidade, iremos utilizar a seguinte fórmula:
\mathrm{\rho_i=\sigma\cdot B\cdot\dfrac{1-\nu^2}{E_s}\cdot I_p}
Onde:
- \mathrm{\sigma}: tensão média na superfície de contato entre fundação e solo;
- B: largura da fundação;
- \mathrm{\nu}: coeficiente de Poisson do maciço de solo;
- \mathrm{I_p}: fator de influência, que varia de acordo com a rigidez e forma da fundação, cujos valores são apresentados abaixo.
Então, vamos calcular termo a termo da formulação! Inicialmente, calcularemos a tensão média na superfície de contato, para isso, basta fazermos a razão da carga na sapata e sua área de base.
\mathrm{\sigma=\dfrac{300kN}{1,50m\cdot1,50m}}
\mathrm{\sigma=133,33 kN/m^2}
O coeficiente de Poisson do maciço pode ser estimado de acordo com a tabela abaixo, seguindo a formulação abaixo:
|
Solo |
\mathrm{\nu} |
|
Areia pouco compacta |
0,2 |
|
Areia compacta |
0,4 |
|
Silte |
0,3-0,5 |
|
Argila saturada |
0,4-0,5 |
|
Argila não saturada |
0,1-0,3 |
Utilizaremos para esse exercício \mathrm{\nu=0,5}.
Agora basta determinarmos o módulo de deformabilidade do solo \mathrm{E_s}. Para isso, utilizaremos a seguinte formulação:
\mathrm{E_s=\alpha\cdot K \cdot Nspt}
Onde \mathrm{\alpha} e K variam de acordo com o solo e podem ser obtidos através das tabelas abaixo.
|
Solo |
\mathrm{\alpha} |
|
Areia |
3 |
|
Silte |
5 |
|
Argila |
7 |
|
Solo |
K (MPa) |
| Areia com pedregulhos |
1,1 |
|
Areia |
0,9 |
|
Areia siltosa |
0,70 |
|
Areia argilosa |
0,55 |
|
Silte arenoso |
0,45 |
|
Silte |
0,35 |
|
Argila arenosa |
0,30 |
|
Silte argiloso |
0,25 |
|
Argila siltosa |
0,20 |
Então, por simplificação, consideraremos a camada como argila siltosa, visto que ela apresenta o menor valor de K para as argilas. Algumas literaturas ainda indicam a utilização de um valor inferior a esse, mas a nível acadêmico, iremos utilizar essa simplificação. Assim, chegamos a:
\mathrm{E_s=7\cdot 0,2 MPa \cdot 12}
\mathrm{E_s=16,8 MPa}
Por fim, com a utilização da tabela abaixo, verificamos que \mathrm{I_p=0,99}.
|
Forma |
Sapata flexível |
Sapata rígida |
||
|
Centro |
Canto |
Médio |
||
|
Circular |
1,00 |
0,64 |
0,85 |
0,79 |
|
Quadrada |
1,12 | 0,56 | 0,95 |
0,99 |
|
L/B=1,5 |
1,36 | 0,67 | 1,15 |
|
|
2 |
1,52 | 0,76 | 1,30 |
|
|
3 |
1,78 |
0,88 |
1,52 |
|
|
5 |
2,10 |
1,05 |
1,83 |
|
|
10 |
2,53 | 1,26 |
2,25 |
|
|
100 |
4,00 | 2,00 |
3,70 |
|
Agora é só aplicar na formulação apresentada no início da questão. Lembrando de ter bastante cuidado com as unidades utilizadas. Aqui, para melhor compreensão, colocarei as unidades no SI.
\mathrm{\rho_i=\sigma\cdot B\cdot\dfrac{1-\nu^2}{E_s}\cdot I_p}
\mathrm{\rho_i=133,33 \cdot10^3\cdot 1,50\cdot\dfrac{1-0,5^2}{16,8\cdot10^6}\cdot 0,99}
\mathrm{\rho_i=8,84\cdot 10^{-3}m}
\mathbf{\rho_i=8,84 mm}
Pronto! O recalque imediato estimado para essa fundação é de 8,84mm !
Exercício 2 – Recalque em várias camadas finitas
Considere agora, a mesma sapata da questão anterior (1,50m x 1,50 m) agora assentada em um solo cujo perfil é apresentado na figura abaixo.
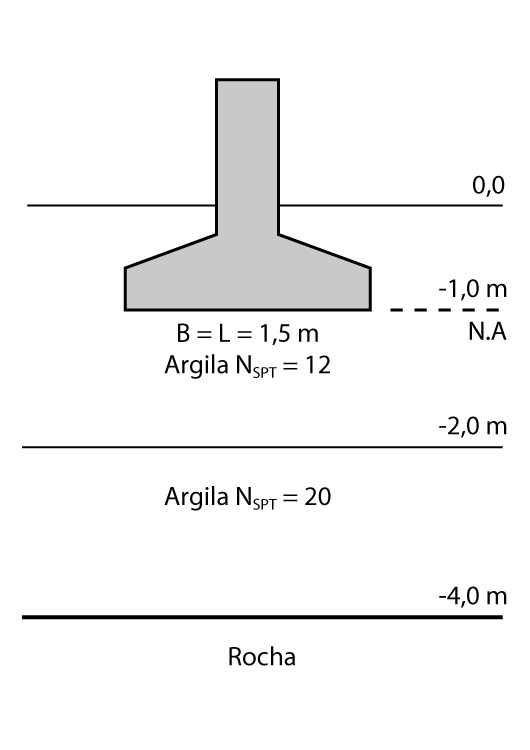
Estime o recalque imediato para tal sapata para a condição apresentada.
Resolução
Essa é uma questão clássica de recalque em camadas finitas para meios elásticos homogêneos. Para a resolução desse exercício, vamos seguir o seguinte passo a passo:
- Estimar o recalque da primeira camada, considerando que o nível -2,0m é o impenetrável para essa camada.
- Considerar uma sapata fictícia na interface das camadas 1 e 2, formada a partir do espraiamento de tensões numa inclinação de 1:2.
- Estimar o recalque para a camada 2.
- Somar o recalque da primeira e segunda camada e assim, estimar o recalque imediato total para essa fundação.
Passo 1
Para estimar o recalque da camada 1, vamos considerar que o impenetrável se encontra na interface entre as camadas 1 e 2. Logo, utilizaremos a formulação de camada finita:
\mathrm{\rho_i=\mu_0\cdot \mu_1\cdot\dfrac{\sigma\cdot B}{E_s}}
Onde:
- \mathrm{\mu_0} e \mathrm{\mu_1}: fatores de influência de embutimento da sapata e de espessura da camada de solo;
Para a primeira camada, temos que h=H=1,0m e B=1,50m. Logo, temos os seguintes valores para a determinação de \mathrm{\mu_0} e\mathrm{\mu_1}:
\mathrm{\dfrac{h}{B}=\dfrac{1,0}{1,5}=0,67}
\mathrm{\dfrac{H}{B}=\dfrac{1,0}{1,5}=0,67}
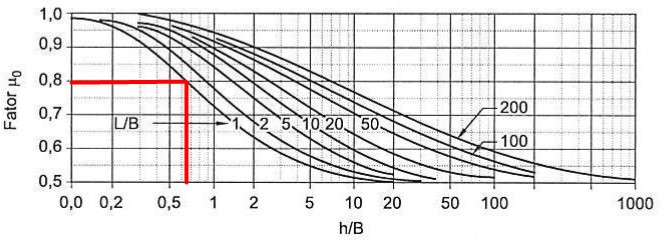
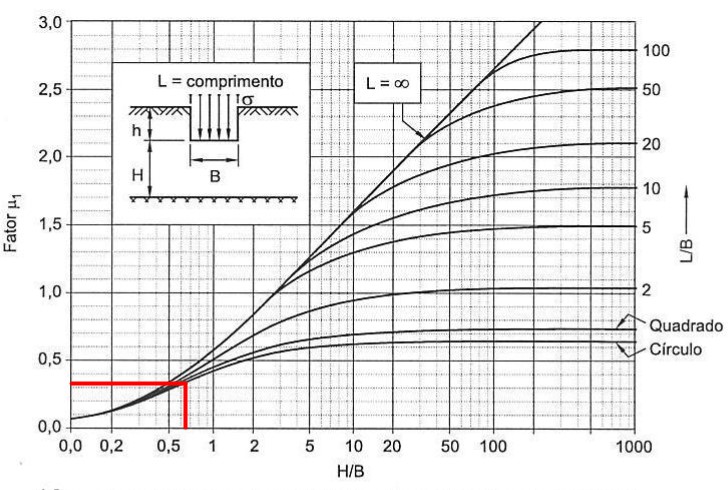
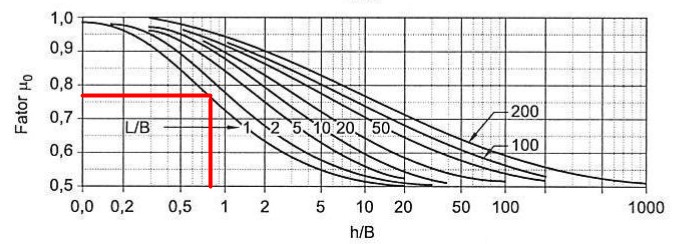
Então, utilizando os ábacos de Janbu, conforme figuras abaixo, temos:
\mathrm{\mu_0=0,80}
\mathrm{\mu_1=0,32}
Como o solo da camada 1 é o mesmo do exercício passado seu módulo de deformabilidade já foi calculado:
\mathrm{E_s=16,8 MPa}
Lembrando que por se tratar também da mesma sapata do exercício anterior, a tensão atuante na sapata é:
\mathrm{\sigma=133,33 kN/m^2}
Então, colocando todos os dados no SI, para não nos perdemos nas unidades, temos:
\mathrm{\rho_{i1}=0,8\cdot 0,32\cdot\dfrac{133,33\cdot10^3\cdot 1,50}{16,8\cdot 10^6}}
\mathrm{\rho_{i1}=3,05 \cdot10^{-3}m}
\mathbf{\rho_{i1}=3,05 mm}
Então, já determinamos o recalque imediato para a camada 1!
Passo 2
Agora, a partir do espraiamento de tensões, iremos considerar uma sapata fictícia na interface de contato entre as camadas 1 e 2.
Para isso, considerando um espraiamento de 1:2, temos a seguinte situação:
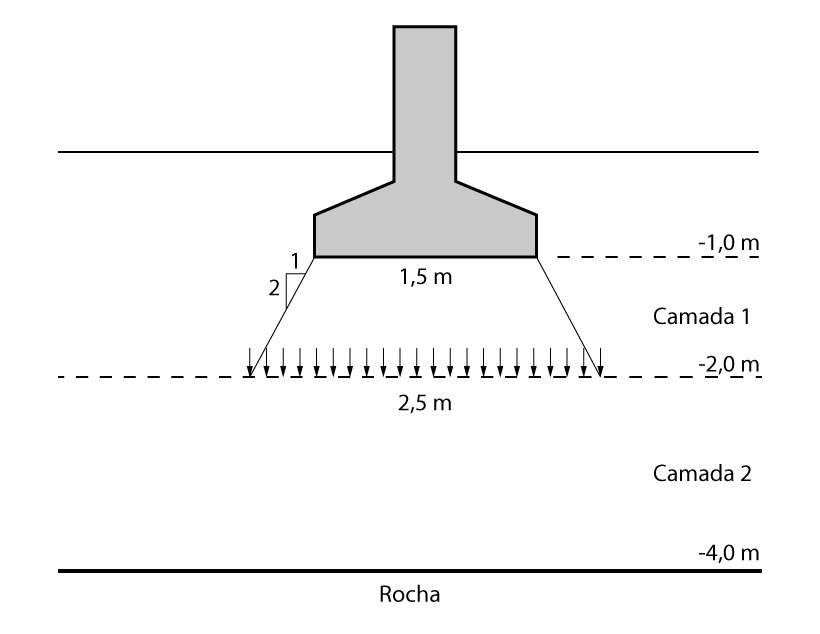
Então, para o cálculo do recalque imediato para a camada 2, teremos uma sapata fictícia com B=2,50m apoiada no topo da camada!
[formulario-recalque]Passo 3
Agora que já sabemos a largura da sapata fictícia, precisamos determinar a tensão atuante nessa sapata!
Sabemos que a carga que vem da superestrutura é a mesma, 300 kN. Logo, para calcular essa nova tensão, basta dividirmos essa carga pela nova área de base:
\mathrm{\sigma'=\dfrac{300kN}{2,50m\cdot2,50m}}
\mathbf{\sigma'=48 kN/m^2}
Agora, iremos calcular o módulo de deformabilidade do solo para a camada 2.
Para isso, iremos utilizar a mesma formulação e tabelas já utilizadas no exercício 1, porém modificando o Nspt para o da segunda camada, que vale 20. Logo, temos:
\mathrm{E_s'=\alpha\cdot K \cdot Nspt}
\mathrm{E_s'=7\cdot 0,2 MPa \cdot 20}
\mathrm{E_s'=28,0 MPa}
Para calcular o recalque imediato então, basta determinar, pelos ábacos de Janbu, os fatores latex]\mathrm{\mu_0}[/latex] e\mathrm{\mu_1}. Então, para a sapata fictícia apoiada no topo da camada 2, temos o seguinte:
\mathrm{\dfrac{h}{B}=\dfrac{2,0}{2,5}=0,80}
\mathrm{\dfrac{H}{B}=\dfrac{2,0}{2,5}=0,80}
Então, utilizando os ábacos de Janbu, conforme figuras abaixo, temos:
\mathrm{\mu_0=0,72}
\mathrm{\mu_1=0,40}
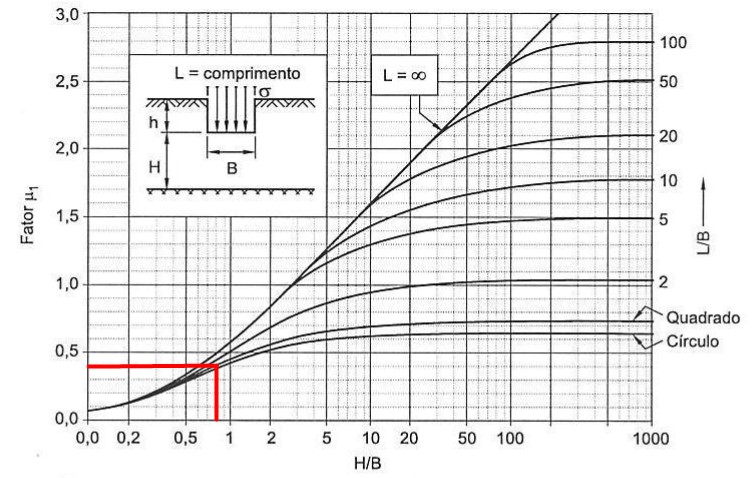
Então, colocando todos os dados no SI, para não nos perdemos nas unidades, temos:
\mathrm{\rho_{i2}=0,72\cdot 0,40\cdot\dfrac{48,0\cdot10^3\cdot 2,50}{28,0\cdot 10^6}}
\mathrm{\rho_{i2}=1,23 \cdot10^{-3}m}
\mathbf{\rho_{i2}=1,23 mm}
Pronto! Já estimamos também o recalque imediato da segunda camada, resultando em 1,23 mm.
Passo 4
Finalmente, basta somarmos os resultados encontrados para o recalque das camadas 1 e 2 para estimarmos o recalque total da fundação:
\mathrm{\rho_{i}=\rho_{i1}+\rho_{i2}}
\mathrm{\rho_{i}=3,05+1,23}
\mathbf{\rho_{i}=4,28 mm}
Pronto! Finalizamos nossa questão! Viu como não tem nenhum segredo estimar recalque em meios elásticos homogêneos de várias camadas?
Espero que você tenha entendido tudo e que esse post tenha te ajudado!
Mas caso tenha ficado alguma dúvida, só comentar que vai ser um prazer responder!
No próximo post vamos resolver alguns exercícios de recalque em areias, com a utilização do Método de Schmertmann.
Se gostou, não deixe de acompanhar a gente aqui, no Youtube e também no Instagram, para ter acesso a mais conteúdos como este!
Por hoje é só, pessoal! Até a próxima!
Engenheiro Civil, Especialista em Estruturas e Fundações. Ex-goleiro, Pseudosommelier de Cervejas e Poeta Freelancer Fajuto.
