Método de Schmertmann: exercício resolvido

Você já conhece o método de Schmertmann para estimativa de recalque em solos arenosos?

Caso a resposta seja negativa, eu aconselho você a dar uma pausa nesse post e ler, inicialmente, nosso post com toda a teoria a respeito desse método!

Mas se você já conhece, vamos direto ao ponto.

Nesse post, resolveremos juntos um mesmo exercício pra os dois métodos de Schmertmann: 1970 e 1978. Dessa forma, além de aprender a utilização de ambos os métodos, iremos discutir as diferenças entre eles.

Você pode acompanhar o conteúdo também através do vídeo que preparamos pra você!

Então, vamos direto à questão!

Exercício proposto

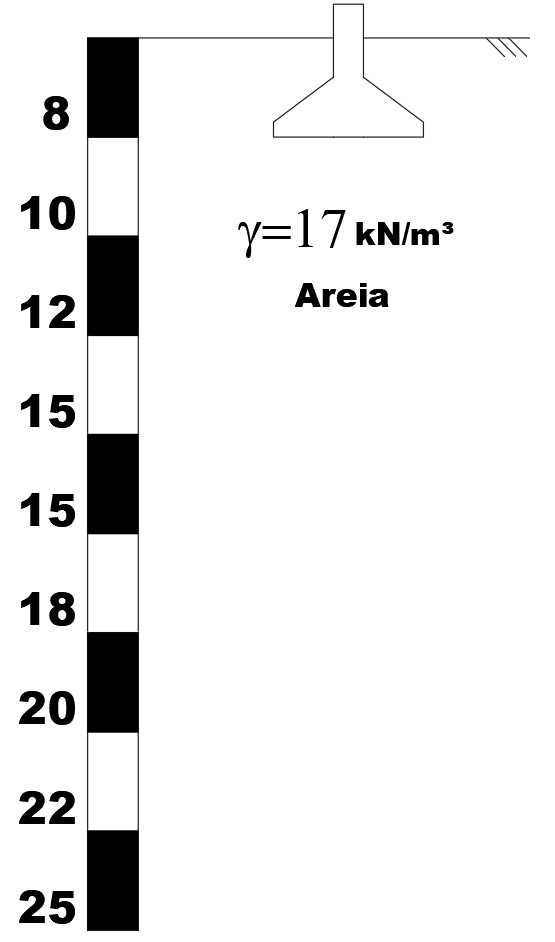
Estime o recalque imediato da sapata indicada na figura abaixo. A sapata é rígida e quadrada, com B=L=2,0m, apoiada na cota de -1,0m, que aplica no solo uma tensão de 0,25 MPa.

Resolução pelo método de Schmertmann (1970)

Bem, relembrando o método de Schmertmann (1970), apresentado anteriormente no post com a teoria, temos que a fórmula geral para a utilização desse método é:

\mathrm{\displaystyle\rho_d=C_1\cdot C_2\cdot\sigma^*\cdot \sum_{i=1}^{n} \left(\dfrac{I_z}{E_s}\cdot \Delta_z \right)_i}

Onde:

• \mathrm{\displaystyle\rho_d}: recalque total;
• \mathrm{\displaystyle {I_z}}: fator de influência à meia altura da i-nésima camada;
• \mathrm{\displaystyle {E_s}}: módulo de deformabilidade da i-nésima camada;
• \mathrm{\displaystyle\Delta_z}: espessura da i-nésima camada;

Então, vamos determinar cada termo da fórmula!

Cálculo de \mathrm{\displaystyle C_1}

Para considerar o embutimento da fundação no cálculo de recalque por meio do Método de Schmertmann, utilizaremos o coeficiente C1, que pode ser determinado através da seguinte formulação:

\mathrm{C_1=1-0,5\cdot\dfrac{q}{\sigma^*}\geq 0,5}

Onde:

• \mathrm{q}: tensão vertical efetiva na cota de apoio da fundação;
• \mathrm{\sigma*}: tensão líquida aplicada pela fundação (\mathrm{\sigma*=\sigma-q})

Como o peso específico da areia em questão é \mathrm{\gamma=17 kN/m^3}, temos que a tensão vertical efetiva na cota de apoio é:

\mathrm{q=17\cdot1,0=17kN/m^2}

Então, podemos afirmar que a tensão líquida vale:

\mathrm{\sigma^*=250 kN/^2-17kN/m^2=233kN/m^2}

Logo:

\mathbf{C_1=1-0,5\cdot\dfrac{17}{233}=0,96}

Cálculo de \mathrm{\displaystyle C_2}

O coeficiente de correção C2 é utilizado para levarmos em conta a ação do tempo no recalque de uma fundação.

Como, para o exemplo em questão, queremos determinar apenas o recalque imediato, podemos assumir que \mathbf{C_2=1,0}.

Cálculo de \mathrm{\displaystyle E_s}

para a estimativa do módulo de deformabilidade podemos usar a formulação simples de Teixeira e Godoy, que associam tal parâmetro com o índice Nspt do solo. A formulação é a seguinte:

\mathrm{E_s=\alpha\cdot K \cdot Nspt}

Onde \mathrm{\alpha} e K variam de acordo com o solo e podem ser obtidos através das tabelas abaixo.

Solo	\mathrm{\alpha}
Areia	3
Silte	5
Argila	7

Solo	K (MPa)
Areia com pedregulhos	1,1
Areia	0,9
Areia siltosa	0,70
Areia argilosa	0,55
Silte arenoso	0,45
Silte	0,35
Argila arenosa	0,30
Silte argiloso	0,25
Argila siltosa	0,20

Então, para o solo em questão temos:

\mathrm{E_s=3\cdot 0,9 \cdot Nspt}

\mathbf{E_s=2,7\cdot Nspt (MPa)}

Cálculo de \mathrm{\displaystyle I_z}

Para a determinação do fator de influência \mathrm{\displaystyle I_z} no método de Schmertmann (1970) utilizamos o seguinte gráfico:

Substituindo para o valor da largura de nossa sapata B=2,0m, temos a configuração apresentada na figura abaixo.

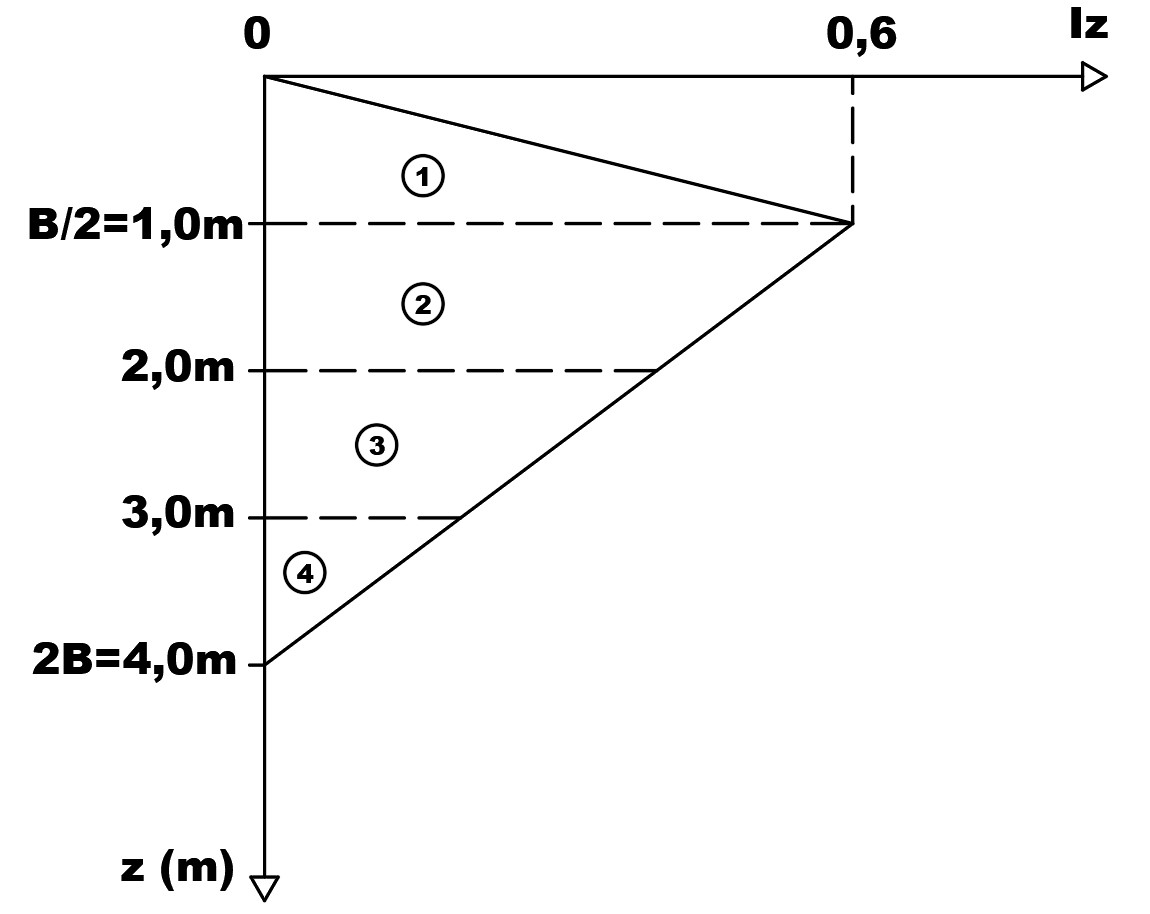
Então, podemos montar uma tabela com os valores de Iz. Lembrando que, para compatibilização de unidades, podemos usar os valores de tensão em MPa e os de comprimento em mm. Logo, temos:

Camada	\mathrm{\Delta_z}(mm)	Iz	Nspt	Es (MPa)	Iz.Az/Es
1	1000	0,3	10	27	11,11
2	1000	0,5	12	32,4	15,43
3	1000	0,3	15	40,5	7,41
4	1000	0,1	15	40,5	2,47

Então, temos todos os dados para aplicar a formulação de Schmertmann (1970).

\mathrm{\displaystyle\rho_d=C_1\cdot C_2\cdot\sigma^*\cdot \sum_{i=1}^{n} \left(\dfrac{I_z}{E_s}\cdot \Delta_z \right)_i}

\mathrm{\displaystyle\rho_d=0,96\cdot 1,0\cdot0,233\cdot (11,11+15,43+7,41+2,47)}

\mathbf{\displaystyle\rho_d=8,15 mm}

Ou seja, o recalque imediato estimado pelo método de Schmertmann (1970) para a sapata apresentada na questão é de 8,15 mm.

[formulario-recalque]

Resolução pelo método de Schmertmann (1978)

O método de Schmertmann de 1978 é um aprimoramento da metodologia anterior. Tal metodologia veio para substituir o método de 1970.

A principal mudança do método de Schmertmann de 1978 para o de 1970 é a determinação do fator de influência Iz. A nova metodologia apresenta novos gráficos para a determinação desse fator, conforme a figura abaixo.

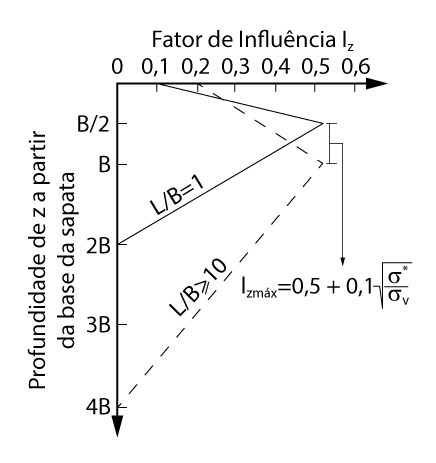
Ou seja, a formulação para o método de 1978 é igual a do método de Schmertmann de 1970. Então, utilizaremos os mesmos valores de C1, C2, \mathrm{\sigma*} e Es já calculados no exemplo anterior.

Iremos apenas calcular diferentes fatores de Iz. Então, o valor de \mathrm{I_{zmáx}} para tal método é calculado como:

\mathrm{I_{zmáx}=0,5+0,1\cdot\sqrt{\dfrac{\sigma^*}{\sigma_v}}}

Onde:

• \mathrm{{\sigma_v}}: tensão vertical efetiva na profundidade correspondente a \mathrm{I_{zmáx}};

Sabemos que nossa sapata apresenta \mathrm{I_{zmáx}} a uma profundidade de 2,0m, logo, para essa profundidade, temos que a tensão vertical efetiva vale:

\mathrm{\sigma_v=\gamma\cdot h}

\mathrm{\sigma_v=17 kN/m^3\cdot2,0m}

\mathrm{\sigma_v=34 kN/m^2=0,034MPa}

Logo:

\mathrm{I_{zmáx}=0,5+0,1\cdot\sqrt{\dfrac{0,233}{0,034}}}

\mathrm{I_{zmáx}=0,76}

Chegamos então ao seguinte gráfico de Iz.

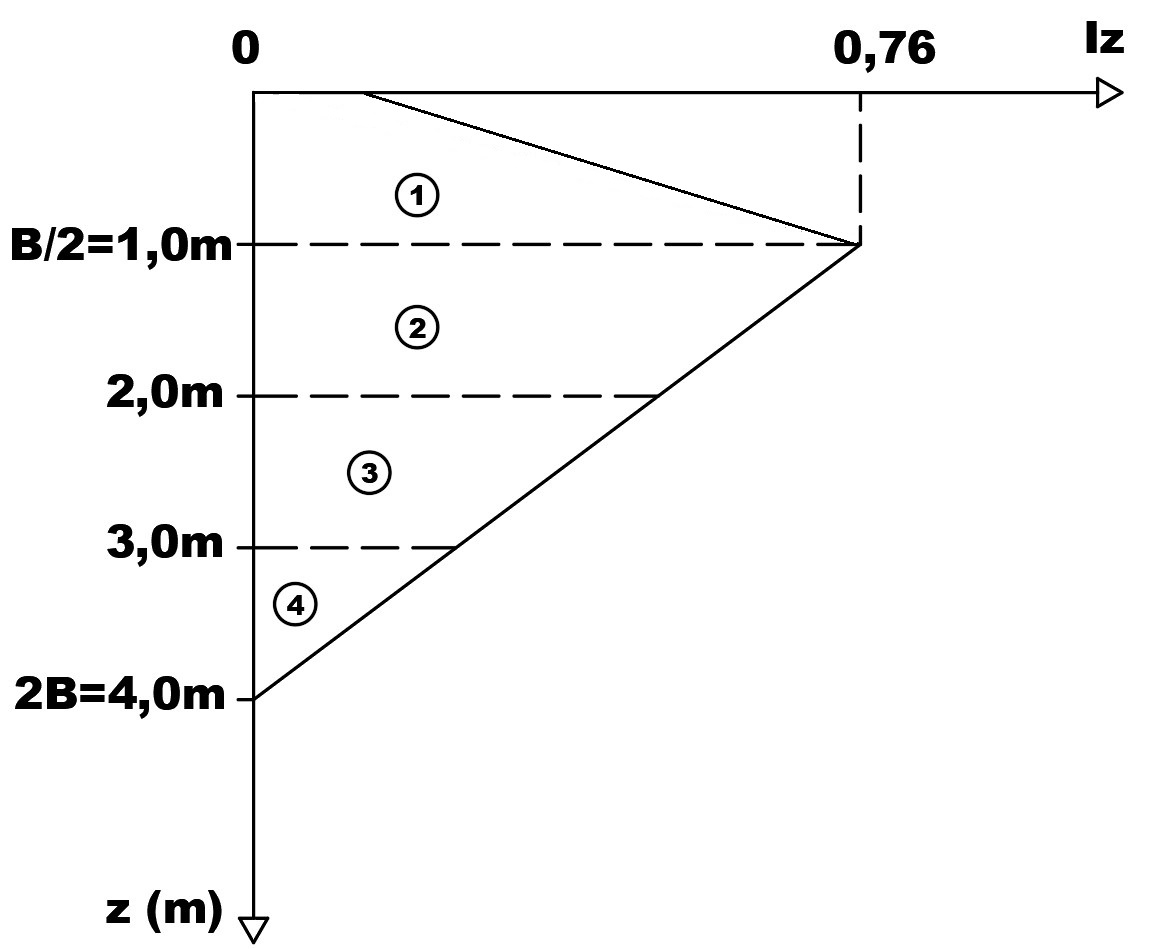
Podemos então, agora, elaborar outra tabela com os valores respectivos de Iz para cada camada:

Camada	\mathrm{\Delta_z}(mm)	Iz	Nspt	Es (MPa)	Iz.Az/Es
1	1000	0,43	10	27	15,93
2	1000	0,63	12	32,4	19,44
3	1000	0,38	15	40,5	9,38
4	1000	0,12	15	40,5	2,96

Pronto! Agora basta aplicarmos a formulação do método de Schmertmann!

\mathrm{\displaystyle\rho_d=C_1\cdot C_2\cdot\sigma^*\cdot \sum_{i=1}^{n} \left(\dfrac{I_z}{E_s}\cdot \Delta_z \right)_i}

\mathrm{\displaystyle\rho_d=0,96\cdot 1,0\cdot0,233\cdot (15,93+19,44+9,38+2,96)}

\mathbf{\displaystyle\rho_d=10,67 mm}

Ou seja, o recalque imediato estimado para a mesma fundação, aplicando agora o método de Schmertmann de 1978 é de 10,67mm.

Estimando o recalque ao longo do tempo

Segundo estudos, em solos arenosos o recalque imediato é responsável pela grande parcela do recalque total do solo.

Porém, podemos estimar esse recalque ao longo do tempo!

Na resolução do nosso exercício, nos atemos a determinar o recalque imediato, logo assumimos o fator C2=1,0.

Para estimarmos os recalques ao longo do tempo para ambos os casos, basta apenas calcularmos C2 para um intervalo de tempo que se deseja estimar o recalque e multiplicar pelo valor de recalque imediato encontrado.

Temos então a seguinte formulação para a determinação de C2.

\mathrm{C_2=1+0,2\cdot log\left(\dfrac{t}{0,1}\right)}

Onde:

• t: tempo em anos.

Ou seja, vamos determinar agora o valor de C2 para um tempo arbitrado de 5 anos.

\mathrm{C_2=1+0,2\cdot log\left(\dfrac{5}{0,1}\right)}

\mathrm{C_2=1,34}

Ou seja, matematicamente isso quer dizer que há, em 5 anos, um acréscimo de 34% de recalque nessa fundação. Logo teremos para ambos os casos analisados.

• Método de Schmertmann (1970): foi encontrado um recalque imediato de 8,15 mm, logo temos que o recalque estimado ao final de 5 anos será de 10,92 mm.
• Método de Schmertmann (1978): foi encontrado um recalque imediato de 10,67 mm, logo temos que o recalque estimado ao final de 5 anos será de 14,30 mm.

Pronto! Viu como não foi difícil utilizar o método de Schmertmann?

Espero que você tenha gostado! Se ainda ficou alguma dúvida, deixa nos comentários que a gente te responde!

Não deixe de seguir nosso blog, assinar nossa newsletter, além de acompanhar nosso canal no Youtube e ficar por dentro das novidades!

Até a próxima!