Geometria de sapatas sob cargas centradas

Uma das soluções de fundações rasas preferidas pelos construtores são as sapatas isoladas, definidas pela ABNT/NBR: 6122 (2019) como elementos de fundação em concreto armado em que as tensões de tração são resistidas pelas armaduras empregadas.

Uma vez que você já obteve os esforços oriundos da superestrutura, a próxima etapa de seu projeto estrutural será a escolha entre as possíveis soluções para a infraestrutura. De acordo com o estudo no solo, é possível optar por fundações rasas ou fundações profundas.

Esse post será uma introdução a essa solução de fundação. Nele você vai aprender como dimensionar a área de base e as alturas de sapatas isoladas submetidas a carga centrada assim como detalhes construtivos para melhorar a exequibilidade das mesmas.

Classificação de sapatas quanto a rigidez

Inicialmente, é necessário compreendermos que o comportamento estrutural das sapatas pode ser organizado de acordo com a rigidez da mesma, podendo ser separadas em sapatas rígidas e flexíveis.

Sapatas rígidas

As sapatas rígidas são aquelas em que pode-se admitir uma distribuição plana de tensões normais no contato entre a sapata e solo. Nestas sapatas, admiti-se que a mesma trabalha à flexão nas duas direções e que ocorre uma distribuição da tração na flexão uniformemente em todas a largura.

Além disso, as sapatas rígidas também trabalham à cisalhamento nas duas direções, não sofrendo ruptura por tração diagonal e sim por compressão diagonal, fato que deve ser verificado em projeto.

A fim de verificar se a sapata em questão pode ser considerada rígida, vamos utilizar a condição fornecida pela norma brasileira.

\mathrm{h \geq \dfrac{A - a_p}{3}}

Onde \mathrm{h} representa a altura da sapata, \mathrm{A} indica a dimensão da sapata em uma das direções e \mathrm{a_p} representa a dimensão do pilar na mesma direção.

Com o propósito de facilitar essa e outras verificações, iremos considerar que o balanço (ou aba) nas duas direções seja o mesmo:

\mathrm{A - a_p = B - b_p}

A consequência prática dessa condição é que a partir das dimensões da base, calcularemos uma altura mínima que garanta que a sapata se comporte como rígida.

Nos projetos usuais, daremos sempre preferência a sapatas rígidas, uma vez que as mesmas são menos deformáveis e menos sujeitas a ruptura por punção.

Sapatas flexíveis

Para sapatas flexíveis, situação não preferível, apesar de ainda trabalhar à flexão em duas direções, não é mais possível considerar a distribuição de tração na flexão uniforme ao longo de toda a largura.

Além desta diferença, ainda é necessário a verificação do fenômeno de punção em sapatas flexíveis.

Cálculo da área de base de sapatas

Agora que você já entendeu algumas considerações sobre o comportamento estrutural de sapatas e também assimilou as diferenças entre sapatas rígidas e flexíveis iremos avançar para o cálculo da área de base que estará em contato com solo.

Para a obtenção da área de base necessária em uma sapata, vamos utilizar a razão entre o esforço característico e a tensão admissível do solo, que pode ser obtida através de correlações com o ensaio SPT.

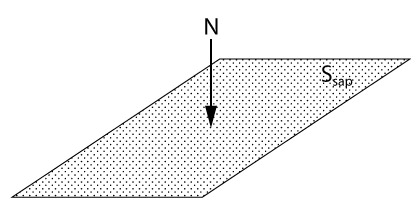
\mathrm{S_{sap} = \dfrac{N}{\sigma_{adm}}}

Como ainda não conhecemos a geometria da sapata, não é possível precisar sobre o peso próprio da mesma. Uma forma de levar em consideração o peso próprio é majorar os esforços por um coeficiente majorador \mathrm{K_{maj}}.

Caso se possua a normal oriunda das cargas permanentes separada da normal decorrente das cargas variáveis, pode-se adotar o \mathrm{K_{maj}=1,10} multiplicando apenas as cargas permanentes, conforme apresentado abaixo:

\mathrm{S_{sap} = \dfrac{1,10 \cdot N_{gk} + N_{qk}}{\sigma_{adm}}} [interesse-fundacoes-rasas]

Em situações em que os esforços decorrentes de cargas permanentes e variáveis estiverem agrupado é recomendado adotarmos \mathrm{K_{maj}=1,05}.

\mathrm{S_{sap} = \dfrac{1,05 \cdot N_{gk+qk}}{\sigma_{adm}}}

Abas iguais nas duas direções

Conforme comentado anteriormente, a fim de facilitar as verificações, iremos considerar os balanços (diferença entre a dimensão da sapata e do pilar em uma direção) com o mesmo comprimento nas duas direções.

\mathrm{A - a_p = B - b_p}

Sabendo disso e sabendo que \mathrm{S_{sap} = A \cdot B}, teremos:

\mathrm{A = B - b_p + a_p}

\mathrm{S_{sap} = (B - b_p + a_p) \cdot B}

\mathrm{B^2 + B \cdot (a_p - b_p) - S_{sap} = 0}

Resolvendo agora a equação do segundo grau:

\mathrm{B = \dfrac{b_p - a_p}{2} + \sqrt{ \dfrac{(a_p - b_p)^2}{4} + S_{sap} }}

Após obter o valor de \mathrm{B}, é possível facilmente calcular \mathrm{A} fazendo \mathrm{A = B - b_p + a_p}.

Determinação da altura da sapata

Conforme já destacado anteriormente, a norma brasileira apresenta uma condição para que possamos considerar a a sapata como rígida:

\mathrm{h \geq \dfrac{A - a_p}{3}}

Como já conhecemos o valor de \mathrm{A} e a dimensão do pilar (\mathrm{a_p}) já é conhecida no momento em que estamos dimensionando a geometria da sapata, é possível calcular um valor mínimo para \mathrm{h}.

Outro limitante da altura é a necessidade de ancorar dentro da sapata a armadura longitudinal do pilar. Para isso, podemos fazer com que a altura útil da sapata seja superior ao comprimento de ancoragem \mathrm{l_b}.

\mathrm{d > l_b}

Determinação da altura do rodapé

Para a altura do rodapé recomenda-se:

\mathrm {h_0 = \left\{ \begin{array}{ll} 20 \; cm \\ \dfrac{h}{3} \end{array} \right. }

Detalhes construtivos

A seguir, você vai aprender alguns detalhes construtivos que são recomendados para uma melhor exequibilidade de sapatas isoladas.

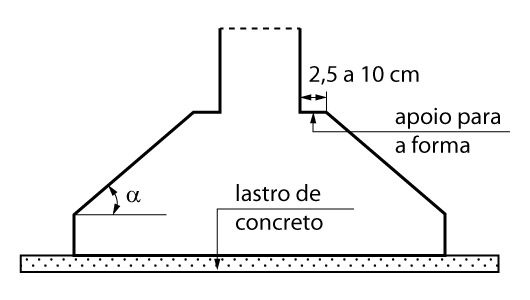
Apoio das formas

Não é recomendado que as dimensões da face da sapata que receberá tenha as esmas dimensões do mesmo, uma vez que haverá necessidade do apoio das formas do pilar para a concretagem deste.

Sendo assim, usualmente utiliza-se valores entre 2,5 cm a 10 cm para cada lado do pilar para calcular as dimensões dessa face.

Angulação limite

Outro ponto importante de se atentar ao calcular as dimensões de uma sapata é respeitar o ângulo de atrito interno do concreto fresco, a fim de dispensar a utilização de formas. Dessa forma, vamos limitar o ângulo apresentado na figura abaixo a 30º.

Lastro de concreto

Por fim, a norma ABNT/NBR: 6122 (2019) exige que todas as partes de uma fundação rasa devam ser concretadas sobre um lastro de concreto não estrutural com espessura mínima de 5 cm.

No geral, o objetivo dessa publicação é fornecer os conhecimentos necessários para realizar o dimensionamento geométrico de sapatas isoladas submetidas a carregamentos centrados.

Se você gostou desse texto ou se ainda possui alguma dúvida, deixe uma mensagem nos comentários abaixo!

---

Fonte:

BASTOS, P. S. S. Sapatas de fundação. 2016 Notas de Aula.

ASSOCIAÇÃO BRASILEIRA DE NORMAS TÉCNICAS. NBR 6122: Projeto e execução de fundações – Procedimento. Rio de Janeiro, 2019.