Se você já acompanha nosso blog há algum tempo, percebeu que já citamos em diversos posts, como no de fundações rasas ou de capacidade de carga de estacas, que podemos determinar a tensão admissível no solo através do laudo de ensaio SPT.
Mas afinal, qual o conceito de tensão admissível e como podemos calculá-la?
Nesse post você aprenderá a calcular a tensão admissível do solo através de alguns métodos.
Te prometo que ao final do post você estará bem mais confiante para a elaboração de um projeto de fundações!
Agora vamos aprender?
Lembrando que você pode acompanhar o conteúdo continuando a leitura do post ou também assistindo o respectivo vídeo que preparamos pra você!
Tensão admissível do solo
Vamos nos questionar inicialmente: o que seria exatamente a tensão admissível do solo?
Bem, para isso, vamos relembrar o conceito de capacidade de carga já apresentado no nosso post sobre estacas.
Capacidade de carga é a tensão transmitida pela fundação ao solo, capaz de causar neste, sua ruptura ou deformação excessiva.
Então, sabendo disso, podemos dizer que a tensão admissível do solo nada mais é do que tal capacidade de carga dividida por um fator de segurança, em que tal fator varia de acordo com o método utilizado para se calcular a capacidade de carga do solo.
Ficou confuso? Vou tentar simplificar para você.
Imagine que a capacidade de carga de um solo, para determinada fundação, seja de 30 tf/m². Isso significa que, para se submetido a tal tensão, o solo sofrerá ruptura ou deformação excessiva.
Como não podemos calcular nossas fundações para esse limite de tensão, dividimos esse valor por um fator de segurança, e assim, calculamos nossas fundações para um valor de tensão, dito, tensão admissível, que é menor do que a tensão que causaria a ruptura do no solo.
Ficou mais claro agora?
Então, agora que você já sabe o conceito de tensão admissível, vamos ver as metodologias para a determinação da mesma.
Como determinar a tensão admissível do solo?
Segundo a NBR 6122:2010, a tensão admissível deve ser fixada a partir da utilização e interpretação de um ou mais dos procedimentos abaixo:
- Prova de carga sobre placa;
- Métodos teóricos;
- Métodos semi-empíricos.
Vale lembrar que além disso, a norma ainda determina que devem ser respeitadas as deformações máximas da estrutura e recalques impostos pela própria norma.
Agora, vamos nos aprofundar um pouco em cada um desses métodos citados acima.
Prova de carga sobre placa
Este ensaio, nada mais é do que uma simulação, no campo, do comportamento da fundação direta sob ação das cargas solicitantes advindas da superestrutura.
De maneira resumida, o ensaio consiste na instalação de uma placa de aço, ou ferro fundido, rígida de 80 cm de diâmetro em que são aplicadas cargas, em diversos estágios, e simultaneamente a essa aplicação, são realizadas anotações dos respectivos recalques do solo.
A partir de tal ensaio, obtém-se um gráfico que relaciona a tensão aplicada ao solo e o recalque no mesmo.
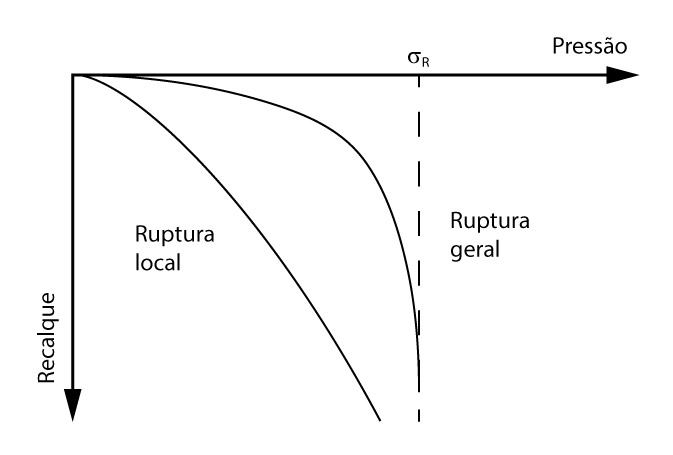
Como você pode perceber pelos gráficos apresentados, a deformação do solo pode ocorrer em duas formas principais.
De um modo, o gráfico de tensão-recalque do solo tem um patamar bem definido, em que, mantida uma tensão constante, os recalques continuam a aumentar. Ou seja, podemos dizer que tais solos possuem capacidade de carga bem definida (\mathrm{{\sigma _R} = 0,4}). Tal modo de ruptura é dito ruptura geral e ocorre principalmente em areias compactas e argilas rijas.
Outro modo de ruptura é dito local. Nesse caso, o solo não tem uma tensão de ruptura bem definida. Tal característica é típica de solos com baixa resistência, como areias fofas e argilas moles.
Mas vamos agora ao que interessa: como vamos determinar a tensão admissível do solo através do ensaio de carga sobre placa?
Isso é bem simples!
Se o solo tiver uma ruptura geral, basta utilizarmos o fator de segurança igual a 2,0. Ou seja, temos que a tensão admissível do solo será:
\mathrm{{\sigma _{adm}} = \dfrac{{{\sigma _R}}}{2}}
Já se tivermos um solo de ruptura local, existem algumas metodologias para a determinação da tensão admissível, apresentaremos aqui o critério de Boston, que consiste matematicamente em:
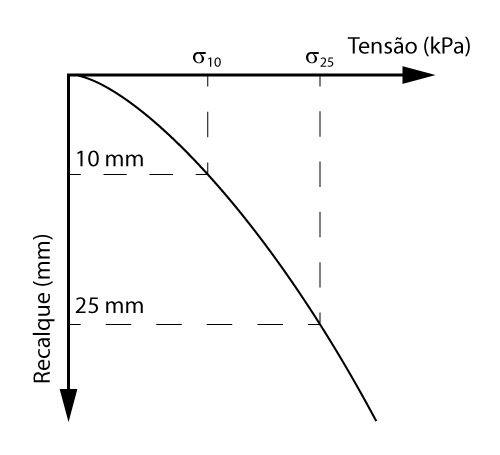
\mathrm{{\sigma _{adm}} \le \left\{ \begin{array}{l}\dfrac{{{\sigma _{25}}}}{2}\\{\sigma _{10}}\end{array} \right.}
Onde:
- \mathrm{{\sigma _{25}}}: tensão responsável por ocasionar um recalque de 25 mm no solo;
- \mathrm{{\sigma _{10}}}: tensão responsável por ocasionar um recalque de 10 mm no solo.
Agora que já sabemos como calcular a tensão admissível no solo através do ensaio de carga sobre placa, vamos para os métodos teóricos.
Métodos teóricos
Os métodos teóricos são formulações para previsão da capacidade de carga desenvolvidas através de análises teóricas.
Como a própria NBR 6122:2010 conceitua, as formulações para determinação da capacidade de carga são desenvolvidas a partir do conhecimento do tipo de ruptura que o solo pode sofrer e das condições de carregamento aos quais é solicitado.
Destacam-se, entre tais formulações, as teorias de Terzaghi, Meyerhoff, Skempton e Vesic.
Nesse post, falaremos exclusivamente sobre a formulação de Terzaghi, porém, se você tiver interesse em aprender sobre os outros métodos, deixa nos comentários, que a gente faz uma força pra te ajudar!
Método de Terzaghi
Terzaghi propôs um modelo de ruptura de solo em que, ao submeter o mesmo sobre uma tensão de ruptura, ocorrerá um puncionamento de uma cunha abaixo da fundação, representada pela região I, da figura abaixo.
Tal puncionamento acarretará empuxos laterais sobre a região II, que transmitirá tais esforços à região III, fazendo com que seja mobilizada uma resistência à cisalhamento do solo ao longo da superfície de ruptura ao longo das regiões II e III.

Através da análise de tal modelo, com a consideração de uma sapata corrida e de uma ruptura geral do solo, chegou a sua formulação inicial.
Após outros estudos, sua teoria foi adaptada também para sapatas isoladas em diversos formatos e para solos com ruptura local, chegando a tal formulação:
\mathrm{{\sigma _R} = c {N_c} {S_c} + q {N_q} {S_q} + 0,5 \gamma B {N_\gamma } {S_\gamma }}
Onde:
- \mathrm{{\sigma _{R}}}: capacidade de carga do solo;
- c: coesão do solo;
- q: tensão efetiva no solo na cota de assentamento (\mathrm{q = \gamma \cdot h} );
- \mathrm{{\gamma}}: peso específico do solo;
- B: dimensão da fundação;
- Ni: fatores de carga obtidos através do ângulo de atrito do solo;
- Si: fatores de forma da fundação.
Os fatores de carga podem ser obtidos pela utilização do ábaco abaixo. Perceba que existem linhas cheias e linhas pontilhadas no ábaco. As linhas cheias são referentes aos solos de ruptura geral, já as linhas pontilhadas são referentes aos solo de ruptura local.
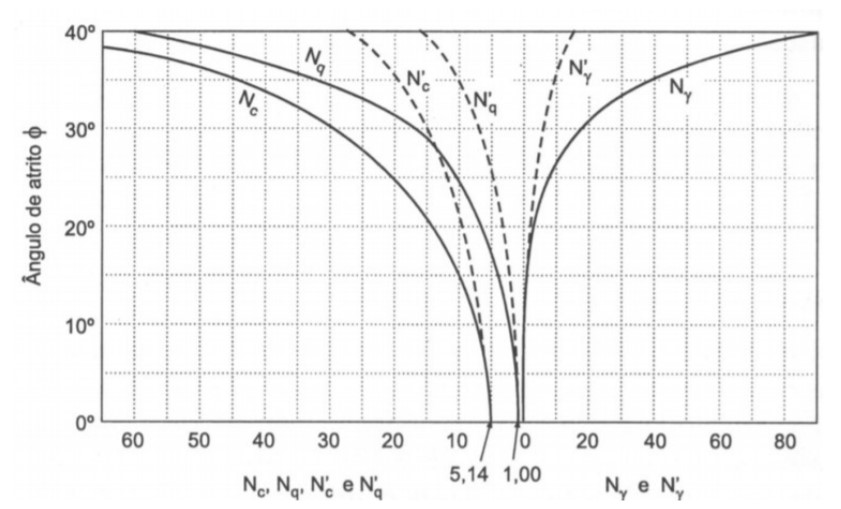
Vale ressaltar que é aconselhável uma adequação dos valores de coesão do solo e do ângulo de atrito do solo:
\mathrm{c' = \dfrac{{2 \cdot c}}{3}}
\mathrm{\tan \phi ' = \dfrac{2}{3} \cdot \tan \phi }
Já os fatores de forma são apresentados na tabela abaixo:
| Forma da fundação |
Fatores de forma |
||
|
Sc |
Sq |
Sγ |
|
| Corrida |
1,0 |
1,0 |
1,0 |
| Quadrada |
1,3 |
0,8 |
1,0 |
| Circular |
1,3 |
0,6 |
1,0 |
| Retangular |
1,1 |
0,9 |
1,0 |
Analisando a formulação de Terzaghi, podemos perceber que a fórmula é dividida em três parcelas principais: uma associada à coesão do solo, outra à sobrecarga do solo e a última relacionada ao atrito entre a fundação e o solo.
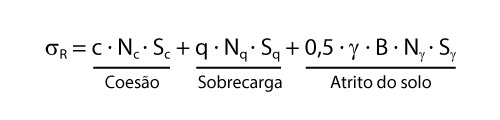
Podemos então, concluir que em um solo puramente coesivo, não haverá a terceira parcela da formulação. Assim como em uma areia pura, sem coesão, a primeira parcela será nula.
Podemos perceber também, que a capacidade do solo não depende só de características do solo, pois depende também da dimensão e forma da fundação, por isso, diz-se que a capacidade de carga é do conjunto fundação-solo.
Agora, por fim, para determinar a tensão admissível do solo através de métodos teóricos, devemos dividir a capacidade de carga calculada pelo fator de segurança de 3,0.
Logo, para o método de Terzaghi, temos que:
\mathrm{{\sigma _{adm}} = \dfrac{{{\sigma _R}}}{3}}
Vale lembrar que ainda existem casos especiais para a utilização dessa fórmula de Terzaghi, por exemplo: presença de solo estratificado e de lençol freático. Mas isso será tema de um post futuro!
Agora, vamos finalmente para os métodos semi-empíricos.
Métodos semi-empíricos
A NBR 6122 conceitua tais métodos como métodos que relacionam resultados de ensaios, como o SPT ou CPT, com tensões admissíveis e que devem ser observados os domínios de validade de suas aplicações, bem como dispersões dos dados e as limitações regionais associadas a cada um dos métodos.
A norma também indica que o fator de segurança a ser adotado para esse tipo de método é igual a 3,0.
Porém, nas correlações mais usuais de projetos de fundações diretas, a formulação para a determinação da tensão admissível já considera um fator de segurança embutido, o que nos dispensa de utilizar esse valor do fator indicado pela norma.
Sabendo disso, vamos apresentar a seguir, três correlações bastante utilizadas de tensão admissível com o Nspt, obtido através do ensaio SPT.
Existem outros métodos também relacionados com CPT, porém, aqui trataremos apenas dos relacionados ao SPT por ser o método mais utilizado no Brasil.
Correlação 1:
\mathrm{{\sigma _{adm}} = \dfrac{{Nspt}}{{50}}\left( {MPa} \right)}
Onde:
- Nspt: valor médio do Nspt no bulbo de tensões, não devendo ser menor que 5 ou maior que 20;
Correlação 2 (Teixeira-96):
\mathrm{{\sigma _{adm}} = 0,05 + \left( {1 + 0,4 \cdot B} \right)\dfrac{{Nspt}}{{100}}\left( {MPa} \right)}
Onde:
- B: lado da sapata quadrada;
- Nspt: valor de Nspt para a profundidade de assentamento da fundação.
Tal formulação foi desenvolvida para sapatas quadradas assentes à 1,5m de profundidade em solos de areia pura e peso específico de 18 kN/m³. Então, pode apresentar valores divergentes à realidade para demais situações.
Correlação 3 (Mello-75):
\mathrm{{\sigma _{adm}} = 0,1 \cdot \left( {\sqrt {Nspt} - 1} \right)\left( {MPa} \right)}
Tal correlação não faz distinção entre o tipo de solo ao ser utilizado, mas não deve ser adotado valores de Nspt inferiores a 4 ou superiores a 16.
Pronto! Viu como determinar a tensão admissível não é nenhum bicho-de-sete-cabeças? Agora você já conhece os diversos métodos utilizados para o cálculo de tal tensão. Nos próximos posts, trataremos ainda sobre esse assunto, com a aplicação prática dos conceitos que você aprendeu aqui e com a presença de solos estratificados.
Caso você ainda tenha alguma dúvida sobre o post ou sugestões para temas futuros, deixa nos comentários que a gente responde!
Não deixe de seguir nosso blog, assinar nossa newsletter, além de acompanhar nosso canal no Youtube e ficar por dentro das novidades!
Até a próxima!
Engenheiro Civil, Especialista em Estruturas e Fundações. Ex-goleiro, Pseudosommelier de Cervejas e Poeta Freelancer Fajuto.

Cara sensacional,meus parabéns a você por dedicar seu precioso tempo para ensinar a nós,muito obrigado!
Bom dia, Thiago. Muito obrigado!
Filipe, que post sensacional! Simples e muito didático.
Parabéns.
Muito bom!!
Opa, Diego, fico feliz que tenha ajudado!
Excelente!!!
Obrigado!
Muito obrigado por sempre acompanhar, Berthier!
Boa tarde, Filipe
Preciso calcular a tensão admissível do solo, sem o uso dos spt.
Existe alguma fórmula em que eu possa relacionar o grau de compactação a 98% do proctor normal ?( o fundo da vala estará compactada a 98%PN e a seção da sapata é 1,0mx1,0m e a profundidade do fundo da vala é 1,75m.
Boa tarde, Luiz. Tudo bem?
Eu acredito que a melhor forma mesmo de você ter o mínimo de segurança na estimativa da tensão admissível do seu solo seria mesmo pelo ensaio de Nspt.
Eu, particularmente, não conheço algum método para determinar a tensão admissível apenas com o grau de compactação, mas procure o material do Prof. Marangon sobre geotecnia das fundações. Nesse material ele aborda algo nesse sentido.
Espero ter ajudado!
Abraço, amigo!
Essa formulação 1, é de qual autor ou norma?
Muito obrigado
Obs: excelente trabalho Parabéns.
Boa tarde! Como calcular a tensão admissível do solo pelo Método da percussão se eu não tiver o dado do S( seção do peso) da fórmula toda, apenas o peso cilíndrico com diâmetro de 0,3 m e massa (P) de 9.000 g. Desde já agradeço. Por favor, preciso da resposta com muita urgência.
Att.
Andréa
Bom Dia, Felipe.
Obrigado por disponibilizar esse conteúdo de forma tão clara.
Você pode me informar os livros em que eu possa me aprofundar no conteúdo ?
Bom dia, Thiago! Sempre recomendo os livros do Prof. Cintra e o livro do Prof. Velloso. Abraço!
Boa noite Filipe,
Muito bom.