Tensão admissível em sapatas: exercício resolvido

Você achou que não teríamos exercício resolvido sobre tensão admissível para sapatas?

Achou errado!

Neste post, aplicaremos todo o conteúdo apresentado no post sobre a teoria de tensão admissível para sapatas. Vamos apresentar um exemplo prático para que você possa aprender a aplicação de todas as formulações apresentadas.

Vamos lá?

Apresentação do problema

Vamos imaginar que você está elaborando o projeto de fundações de uma edificação. Então, o mínimo que você deve ter em mãos, além das solicitações advindas da superestrutura é o laudo de sondagem local.

Então, vamos supor que perfil geotécnico de um dos furos de sondagem é o apresentado a seguir.

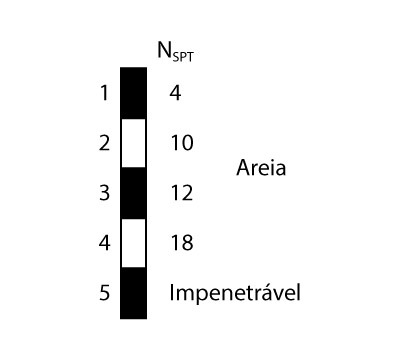
Então, a partir desse perfil, calcularemos agora pelo método de Terzaghi e correlações semi-empíricas a tensão admissível para uma sapata de 1,0 m x 1,0 m assentada a 2,0 metros de profundidade.

Vale ressaltar, que para o cálculo a partir de algumas correlações semi-empíricas, a dimensão da fundação não é necessária, porém, para o cálculo pelo método de Terzaghi, utilizaremos tal dado.

Mas lembrando que o cálculo da tensão admissível sempre é necessário para o adequado dimensionamento das sapatas.

Tensão admissível pelo Método de Terzaghi

Como vimos no post sobre os métodos de determinação da tensão admissível, a formulação da capacidade de carga de Terzaghi para uma sapata isolada é:

\mathrm{{\sigma _R} = c  {N_c}  {S_c} + q  {N_q}  {S_q} + 0,5  \gamma  B  {N_\gamma } {S_\gamma }}

Onde:

• \mathrm{{\sigma _{R}}}: capacidade de carga do solo;
• c: coesão do solo;
• q: tensão efetiva no solo na cota de assentamento (\mathrm{q = \gamma \cdot h});
• \mathrm{{\gamma}}: peso específico do solo;
• B: dimensão da fundação;
• N_i: fatores de carga obtidos através do ângulo de atrito do solo;
• S_i: fatores de forma da fundação.

O primeiro passo para a resolução pelo método de Terzaghi é determinar a coesão, o ângulo de atrito e o peso específico do solo.

O ideal seria a realização de ensaios para a determinação desses parâmetros. A nível acadêmico, podemos fazer uso de correlações para a determinação dos parâmetros. Nessa resolução utilizaremos a tabela abaixo, encontrada no material do Prof. Marangon.

Areias e solos arenosos
Compacidade	\mathrm{\gamma}(kN/m³)	C (kN/m²)	\mathrm{\phi} (\mathrm{^o})
Fofa	16,0	0	25-30
Pouco compacta	18,0	0	30-35
Medianamente compacta	19,0	0	35-40
Compacta	20,0	0	40-45
Muito compacta	>20,0	0	>45

Para um solo arenoso com Nspt igual a 10, a norma NBR 6484:2001 o classifica como medianamente compacto. Logo, iremos adotar para essa questão:

• coesão: 0,0;
• ângulo de atrito: 36 \mathrm{^o};
• peso específico: 19 kN/m³.

De posse do ângulo de atrito do solo, poderemos obter os fatores de carga.

Como estamos tratando de uma fundação assente a 2,0 metros de profundidade em um solo arenoso com Nspt equivalente a 10, podemos considerá-lo um solo de ruptura geral, logo, para ao usarmos o ábaco dado abaixo, utilizaremos as linhas cheias para a determinação dos fatores de carga.

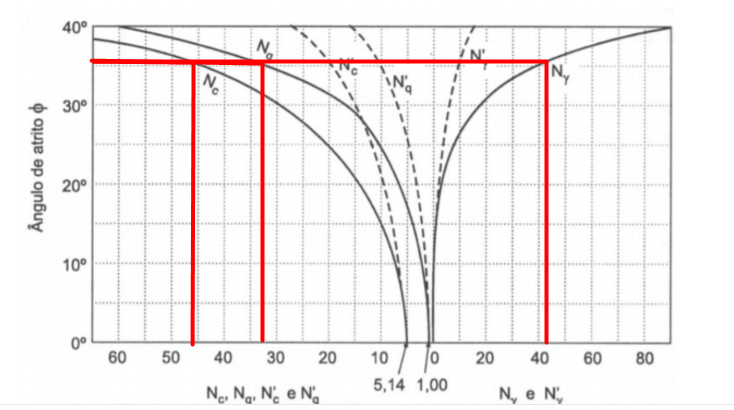
Temos então:

• N_c = 46;
• N_q = 33;
• \mathrm{{N_{\gamma}}} = 42

Então, agora precisamos apenas dos fatores de forma para a aplicação da formulação do método de Terzaghi, Utilizando da tabela de fatores de forma abaixo, iremos adotar os valores dos fatores de forma correspondentes à linha da fundação quadrada.

Forma da fundação	Fatores de forma
	Sc	Sq	Sγ
Corrida	1,0	1,0	1,0
Quadrada	1,3	0,8	1,0
Circular	1,3	0,6	1,0
Retangular	1,1	0,9	1,0

Pronto, agora já temos todas as variáveis para a determinação da capacidade de carga pelo método de Terzaghi. Temos então:

\mathrm{{\sigma _R} = c  {N_c}  {S_c} + q  {N_q}  {S_q} + 0,5  \gamma  B  {N_\gamma } {S_\gamma }}

\mathrm{{\sigma _R} =  2\cdot 19,0 \cdot 33,0\cdot 0,8 +9,5\cdot 1,0\cdot 42,0 \cdot 1,0}

\mathrm{{\sigma _R} =  1402,2 kN/m²}

Vale perceber que a parcela correspondente a coesão na fórmula foi igualada a zero, devido a coesão nula adotada por se tratar de um solo arenoso.

[interesse-fundacoes-rasas]

Vale lembrar também que tal formulação nos dá a capacidade de carga do solo, que é a tensão que leva o solo à ruptura ou deformação excessiva. A nível de projeto, é indicado sempre trabalharmos com a tensão admissível, que nada mais é do que a capacidade de carga dividida por um fator. Para métodos teóricos, temos:

\mathrm{{\sigma _{adm}} = \dfrac{{{\sigma _R}}}{3}}

Logo, para nossa questão, obtemos:

\mathrm{{\sigma _{adm}} = 467,4 kN/m²}

Agora, vamos resolver essa questão através das correlações empíricas e comparar com o valor encontrado para o método de Terzaghi.

Tensão admissível por métodos semi-empíricos

No post teórico sobre os métodos de determinação da tensão admissível, apresentamos três formulações que serão listadas a seguir:

Correlação 1 : \mathrm{{\sigma _{adm}} = \dfrac{{Nspt}}{{50}}\left( {MPa} \right)}

Correlação 2 (Teixeira-96) : \mathrm{{\sigma _{adm}} = 0,05 + \left( {1 + 0,4 \cdot B} \right)\dfrac{{Nspt}}{{100}}\left( {MPa} \right)}

Correlação 3 (Mello-75) : \mathrm{{\sigma _{adm}} = 0,1 \cdot \left( {\sqrt {Nspt} - 1} \right)\left( {MPa} \right)}

Como você percebe, são aplicações matemáticas simples, geralmente variando unicamente com o Nspt do solo na profundidade de assentamento adotada.

Aplicando o Nspt igual a 10, para a profundidade adotada de 2,0 metros, temos os seguintes resultados:

Correlação 1 : \mathrm{{\sigma _{adm}} = 0,2 MPa = 200 kN/m²}

Correlação 2 (Teixeira-96) : \mathrm{{\sigma _{adm}} = 0,19 MPa = 190 kN/m²}

Correlação 3 (Mello-75) : \mathrm{{\sigma _{adm}} = 0,216 MPa = 216 kN/m²}

Conclusão

Então, para uma sapata quadrada de 1,0 m x 1,0 m assentada a 2,0 metros de profundidade, determinamos a tensão admissível do conjunto sapata-solo através do método teórico de Terzaghi e por três formulações semi-empíricas.

Para o método de Terzaghi, encontramos o valor de \mathrm{{\sigma _{adm}}} = 467,4 kN/m². Já para as formulações semi-empíricas, a média dos valores encontrados foi de 202 kN/m².

Podemos concluir também que, para o perfil de solo analisado, os resultados da tensão admissível no solo para os três métodos semi-empíricos foram bem próximos, apresentando uma congruência entre as três formulações.

Já comparando o resultados obtidos pelos métodos semi-empíricos com o resultado obtido pelo método teórico de Terzaghi, podemos apontar uma grande discordância, sendo os métodos semi-empíricos bem mais conservadores para o perfil de solo analisado.

Vale ressaltar que esse é apenas um exemplo para a aplicação das formulações e melhor entendimento do conteúdo apresentado!

Espero que você tenha gostado do conteúdo e que você tenha conseguido tirar todas as suas dúvidas!

Nos próximos posts trataremos sobre o cálculo da tensão admissível do solo em solos estratificados e com a presença de água!

Caso você ainda tenha alguma dúvida sobre o post ou sugestões para temas futuros, deixa nos comentários que a gente responde!

Não deixe de seguir nosso blog, assinar nossa newsletter, além de acompanhar nosso canal no Youtube e ficar por dentro das novidades!

Até a próxima!