Olá, engenheiros!
Nesse post, iremos lhe mostrar mostrar as diferenças entre uma estrutura hipostática, isostática e hiperestática.
Mas antes, é claro, lhe explicaremos os tipos de apoios e as condições de estabilidade de uma estrutura.
Boa leitura.
Condições de equilíbrio estático
Então pessoal, antes de apresentarmos a diferença entre os tipos de estrutura, precisamos primeiramente conhecer as condições de equilíbrio estático, que são duas.
Primeira condição
A primeira condição necessária para que uma estrutura esteja em equilíbrio é que a soma de todas as forças que atuam sobre ela seja zero, ou seja, essa forças devem se anular.
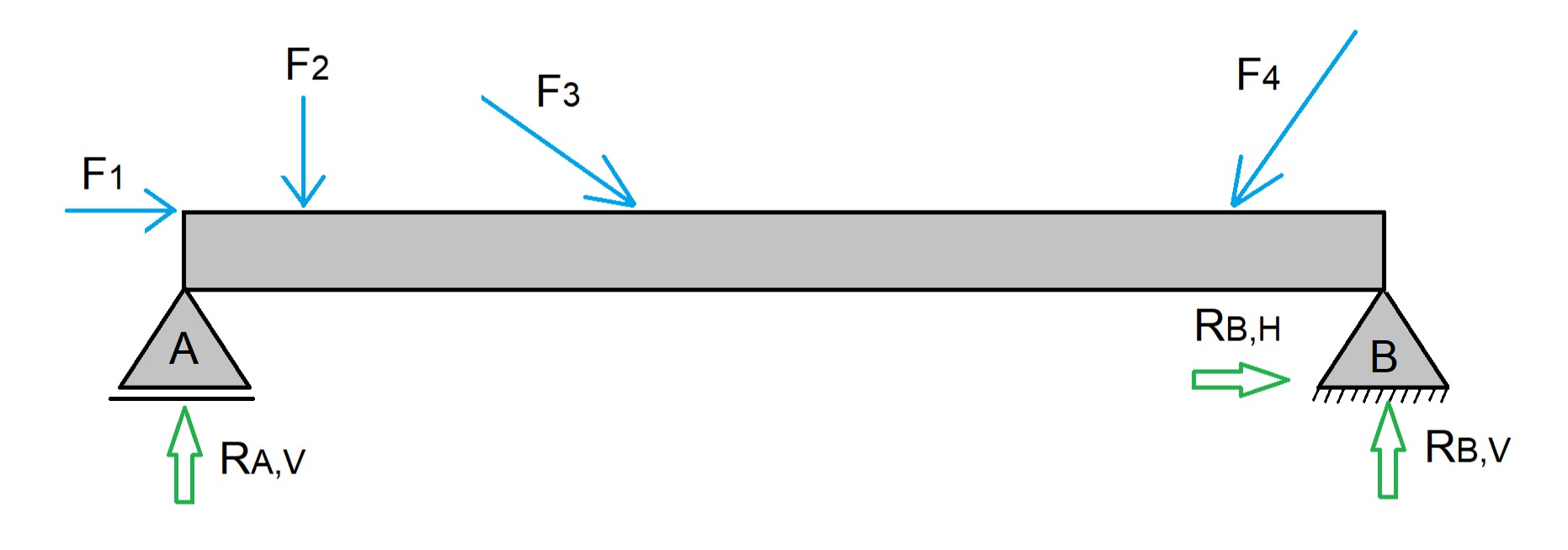
Segunda condição
Já a segunda condição necessária para que uma estrutura esteja em equilíbrio é que a soma dos momentos (ou torque) em relação a um ponto qualquer dessa estrutura também seja zero.
Sendo o momento a grandeza calculada pelo produtor entre a força aplicada perpendicularmente em determinado ponto pela distância entre o ponto de aplicação da força e o eixo de rotação, conforme imagem abaixo.
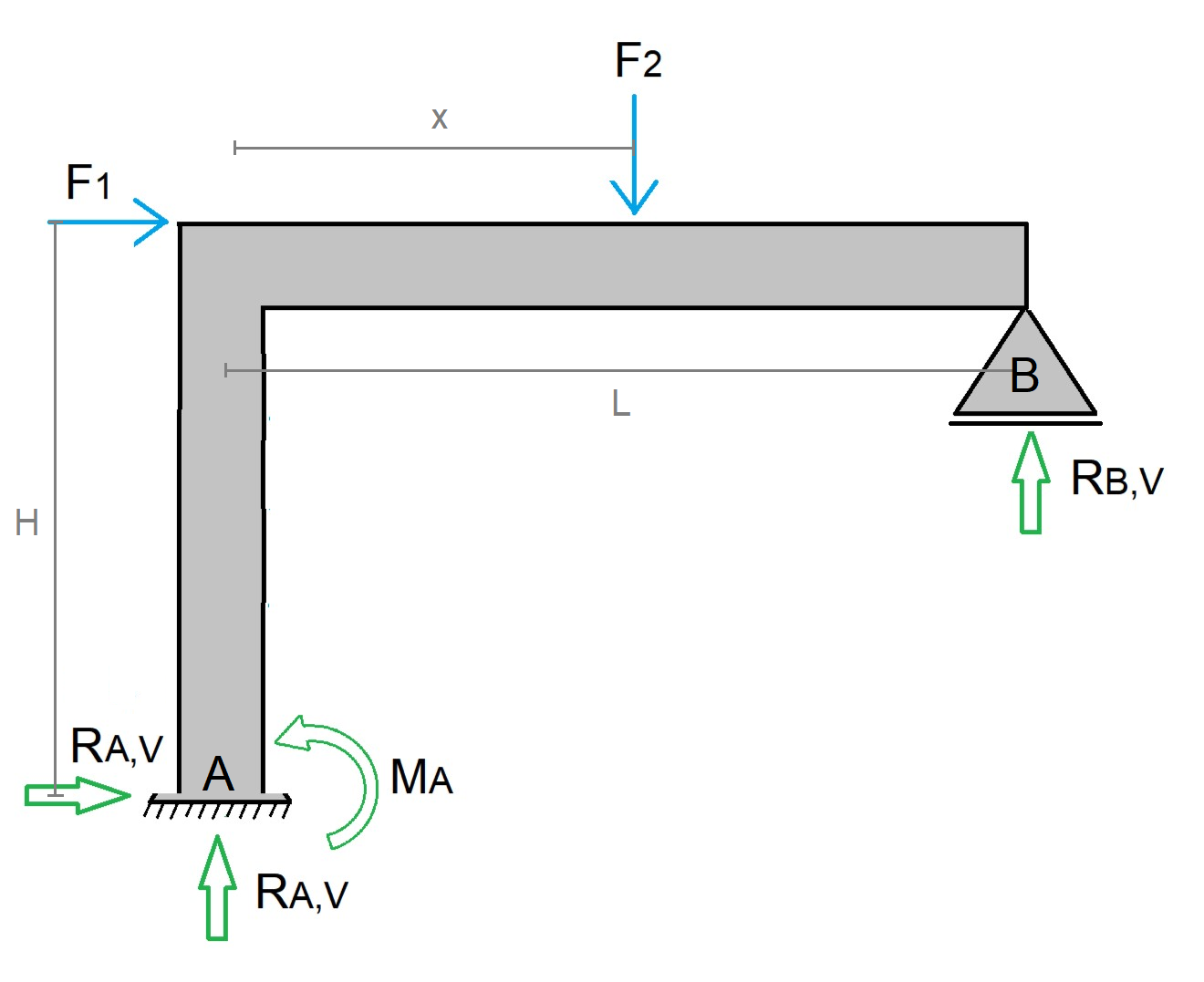
Nessa imagem, a soma dos momento em relação ao apoio A pode ser calculada por:
\mathrm{ΣM_A=-F_1.H-F_2.x+R_{B,V}.L=0}
Agora que já conhecemos as condições de equilíbrio, podemos extrair disso as três equações fundamentais da estática para que possamos entender a estabilidade das estruturas. São elas:
1) A soma das forças horizontais que atuam na estrutura deve ser nula:
\mathrm{ΣFx=0}
2) A soma das forças verticais que atuam na estrutura deve ser nula:
\mathrm{ΣFy=0}
3) A soma das momentos que atuam na estrutura, em relação a um ponto p, deve ser nula:
\mathrm{ΣMp=0}
Tipos de apoio
Sabendo disso, iremos agora conhecer os tipos de apoio para, com isso, saber o grau de restrição da estrutura.
Isso será importante no momento de determinarmos o grau de estaticidade da estrutura.
Apoio do 1º gênero
Esse tipo de apoio é assim classificado quando consegue restringir apenas o deslocamento vertical, mas permite o deslocamento horizontal e a livre rotação da estrutura.
É por esse motivo que recebe o nome de primeiro gênero e, portanto, possui apenas 1 reação de apoio na direção do deslocamento impedido, ou seja, na direção vertical e que chamaremos de RV.
Essa situação ocorre, por exemplo, quando temos a estrutura apoiada sobre um rolo lubrificado que impede apenas o deslocamento vertical, conforme mostra o esquema abaixo.
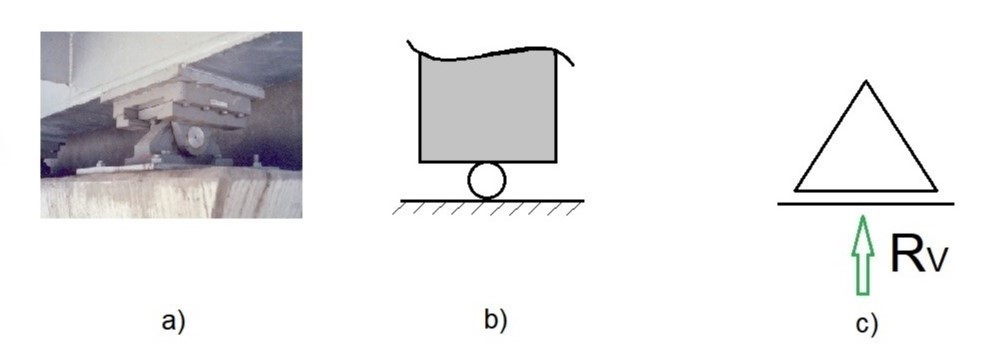
Apoio do 2º gênero
Esse tipo de apoio é assim classificado quando consegue restringir as translações horizontais e verticais, permitindo apenas a rotação da estrutura.
É por esse motivo que recebe o nome de segundo gênero e, com isso, possui 2 reações de apoio na direção dos deslocamentos impedidos e que chamaremos de RV, RH.
Essa situação ocorre, por exemplo, quando temos a estrutura apoiada sobre uma chapa presa completamente ao plano-suporte, conforme mostra o esquema abaixo.
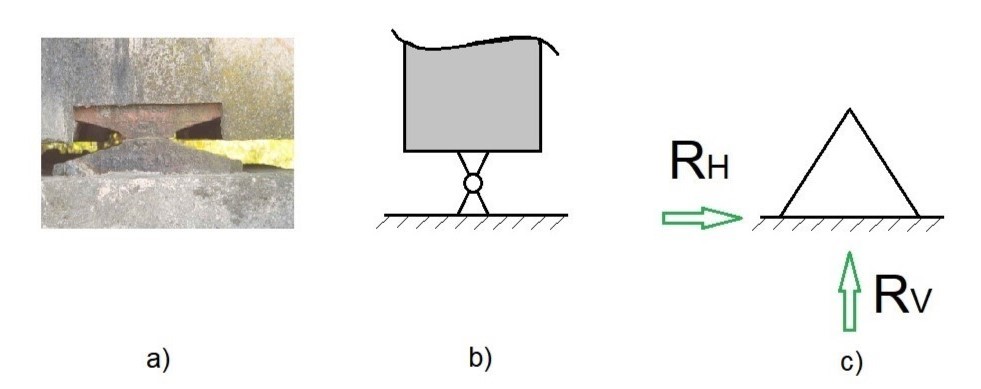
Apoio do 3º gênero
Esse tipo de apoio também é chamado de engaste e é assim classificado quando consegue restringir todos os movimentos possíveis da estrutura, ou seja, as translações horizontais e verticais e a rotação.
É por esse motivo que recebe o nome de terceiro gênero e, portanto, possui 3 reações de apoio na direção dos 3 movimentos impedidos, que chamaremos de RH, RV e M.
Essa situação ocorre, por exemplo, quando ancoramos um elemento estrutural em outro de elevada rigidez, conforme mostra o esquema abaixo.

Estaticidade das estruturas
Agora que já sabemos as condições de estabilidade e quais as reações de apoio devem ser calculadas para cada situação, estamos prontos para classificar as estruturas conforme o grau de estaticidade, sabendo que existem 3 tipos: as estruturas hipostáticas, as isostáticas e as hiperestáticas.
Estrutura hipostática
As estruturas hipostáticas, simplificadamente, são aquelas em que o número de reações de apoio é inferior ao número de equações de equilíbrio disponíveis. Usualmente, as equações disponíveis são apenas 3, mas em alguns casos pode haver mais equações se, por exemplo, existir rótulas na estrutura.
Para as estruturas hipostáticas, geralmente, há instabilidade. Isso porque os apoios são insuficientes para restringir os movimentos da estrutura, como vimos no início do post.
Mas pode ocorrer também que o próprio carregamento da estrutura consiga impedir os graus de liberdade que os apoios não forem capazes de impedir. Nesse caso, há o que chamamos de equilíbrio instável.
Há também a possibilidade de a estrutura possuir reações de apoio superiores ao número de equações e, ainda assim, ser classificada como hipostática por causa da sua instabilidade, como veremos adiante.
Resumidamente, classificamos as estruturas hipostáticas pelo número de reações de apoio insuficientes e pela sua instabilidade. Em razão disso, as estruturas hipostáticas não são usadas em construções.
Estrutura isostática
Já as estruturas isostáticas são aquelas em que o número de reações de apoio é igual ao número de equações de equilíbrio disponíveis, ou seja, o sistema é determinado.
No entanto, precisamos nos atentar que esse critério não é condição suficiente para afirmarmos o grau de estaticidade da estrutura. Também precisamos analisar sua estabilidade.
Portanto, vejamos o exemplo abaixo:
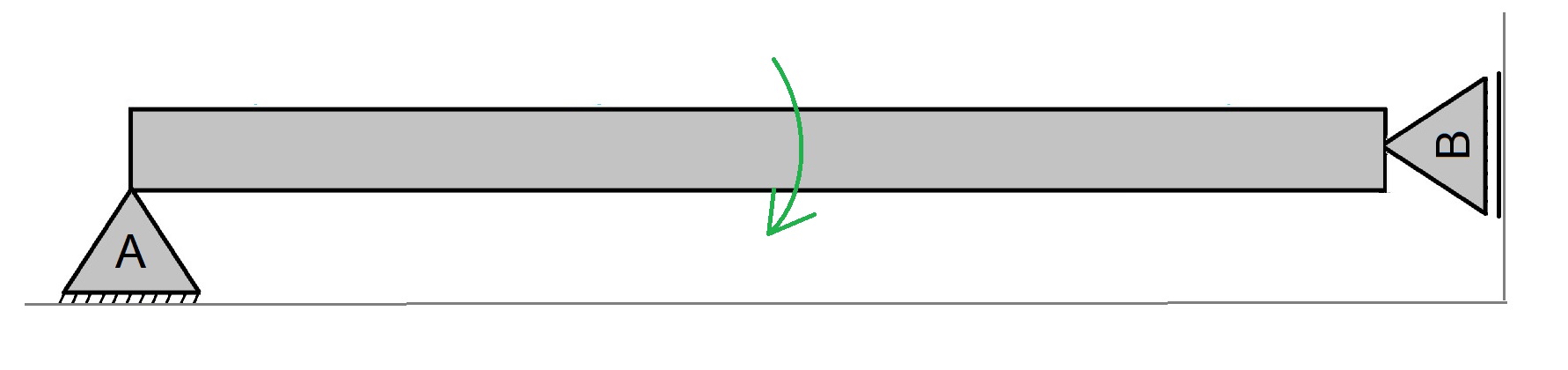
Na estrutura da figura acima, embora o número de reações de apoio seja 3, igual o número de equações disponíveis, ela não é considera isostática, pois não há estabilidade.
Isso ocorre porque não há apoios suficientes para restringir a rotação e, portanto, a estrutura é hipostática.
Estrutura hiperestática
Por fim, as estruturas hiperestáticas são aquelas em que o número de reações de apoio é maior que o número de equações de equilíbrio disponíveis, ou seja, o sistema é indeterminado.
Nessa situação, assim como nas estruturas isostáticas, o equilíbrio deverá estar garantido para que a estrutura seja classificada como hiperestática. Caso contrário, será também hipostática, como na imagem abaixo.
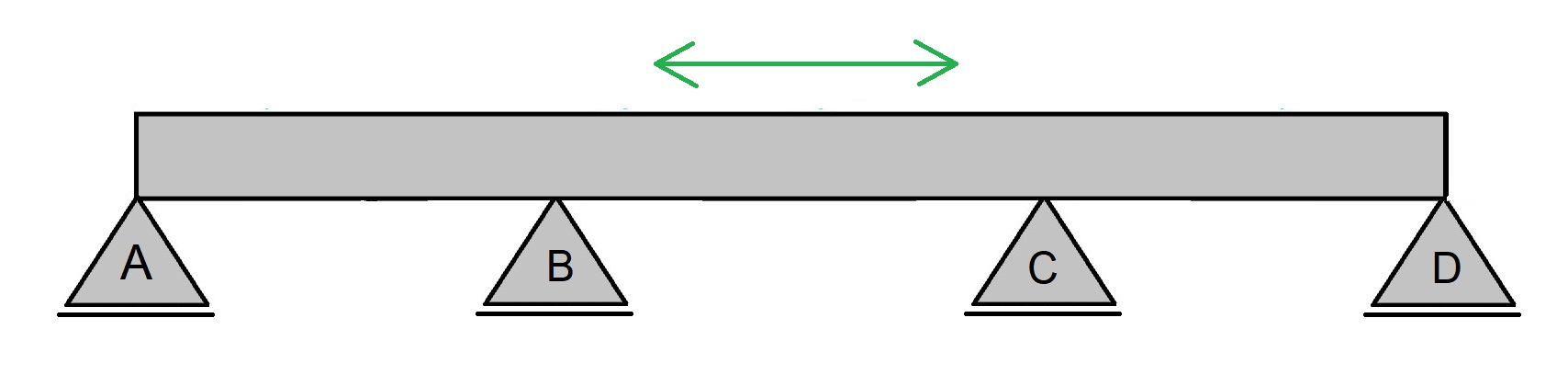
A estrutura acima, composta por apenas apoios de 1º grau, embora esteja aparentemente estável, é também hipostática por não restringir o movimento de translação na horizontal. Já o movimento de rotação não precisa ser restrito pois a configuração dessa estrutura, por si só, já impede esse movimento.
Em síntese, o critério de classificação das estaticidade de acordo com o número de reações de apoio é válido, desde que seja excluída, previamente, a possibilidade de a estrutura ser hipostática.
Pois bem pessoal, essas foram algumas considerações sobre a estaticidade das estruturas, espero muito que esse post tenha sido útil pra você.
Se gostou, siga a gente aqui, no Youtube e também no Instagram e deixe comentários aqui se ficar alguma dúvida.
A gente se vê num próximo post!
Fonte:
SÜSSEKIND, José Carlos. Curso de análise estrutural – Vol. 1. 6. ed. Rio de Janeiro: Globo, 1981.

Engenheira Civil pela Universidade Federal do Piauí, engenheira de obra, perita judicial e pós-graduanda em Avaliação, Auditoria e Perícias de Engenharia.

Excelente explicação!
Muito obrigada, Sara.
Muito obrigado pela sua explicação. É simples, direta e bem fundamentada.
Posso fazer uma pergunta ?
Estou a finalizar um trabalho de investigação que já está na fase final de patentear um novo sistema construtivo. Quanto aos sistemas convencionais , designadamente em betão as forças que integram a estrutura nos vários andares distribuem-se só no estrutura vertical ou existe uma percentagem que apoia e assenta também na estrutura horizontal de cada andar ?
Muito obrigado
Jorge Semedo (Arquitecto)
[email protected]
Jorge, não sei se entendi muito bem a sua dúvida, mas as cargas se distribuem para a laje, depois para as vigas, depois para os pilares e fundações até chegar ao solo. O que significa que elas não se distribuem somente no estrutura vertical.
Adorei as explicações, simples mas eficientes!!!
Prof. Mascarenhas
Eu aprendi com o melhor! Muito obrigada, professor Mascarenhas.
Muito bom, parabéns