Se você já conhece as formulações envolvidas no dimensionamento de uma viga T, esse post irá elucidar as dúvidas restantes através de exemplos práticos. Utilizaremos uma mesma viga submetida a três momentos solicitantes, a fim de analisar as três situações estudadas: linha neutra caindo na mesa, linha neutra caindo na alma sem utilização armadura dupla e linha neutra caindo na alma com utilização de armadura dupla.
Apresentação do problema
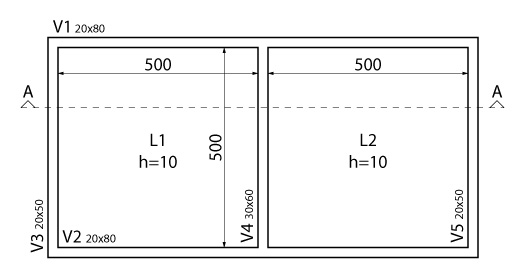
Para o pavimento apresentado na figura abaixo, deseja-se dimensionar a armadura de flexão da viga central V4, levando em consideração a contribuição da laje.
Caso prefira, você também pode acompanhar a resolução pelo vídeo abaixo!
Geometria da Viga T
Para o cálculo da largura colaborante utilizaremos a distância entre as faces da viga central e das vigas de borda, \mathrm{b_2 = 500 \;cm}, e a distância entre dois pontos de momento nulo na viga, que para o caso de uma viga biapoiada, vale o próprio vão efetivo da mesma:
\mathrm{a = 1,00 \cdot l = 520 \; cm}
Podemos então calcular o valor que deve ser acrescido a largura da viga para cada direção da mesma:
\mathrm { b_1 \leq \left\{ \begin{array}{ll} 0,5 \cdot b_2 \\ 0,1 \cdot a \end{array} \right. }
\mathrm { b_1 \leq \left\{ \begin{array}{ll} 250 \; cm \\ 52 \; cm \end{array} \right. = 52 \; cm}
Sendo assim, a largura colaborante da viga T vale:
\mathrm{b_f = b_w + 2 \cdot b_1}
\mathrm{b_f = 30 + 2 \cdot 52 = 134 \; cm}
Assim sendo, a geometria final da viga T que será dimensionada é apresentada na figura abaixo.
Será considerada uma distância de 6,5 cm do centro de gravidade das armaduras tracionadas até a borda mais tracionada e uma distância de 4,25 cm do centro de gravidade das armaduras comprimidas até a borda mais comprimida.
Primeira situação para a viga T
Para o primeiro caso, vamos considerar que o momento de cálculo máximo atuante na viga seja \mathrm{M_{Sd} = 30.000 \; kN \cdot cm}.
É importante se atentar que, aqui estamos nos limitando apenas a obtenção das áreas de aço necessária para resistir aos esforços de flexão. Além desse dimensionamento, outras verificações devem ser realizadas, como por exemplo: dimensionamento e verificação dos esforços de cisalhamento e verificação dos estados limites de serviço.
Cálculo da linha neutra
Assumindo que a linha neutra cairá na mesa, vamos calcular a profundidade da mesma para uma largura igual a \mathrm{b_f}:
\mathrm{k=\dfrac{M_{Sd}}{b_f \cdot f_{cd}}}
\mathrm{k=\dfrac{30000}{134 \cdot \dfrac{2}{1,4}} = 156,72 \; cm^2}
\mathrm{x = \dfrac{0,68 \cdot d \pm \sqrt{0,4624 \cdot d^2 - 1,088 \cdot k}}{0,544}}
\mathrm{x = \dfrac{0,68 \cdot 43,5 \pm \sqrt{0,4624 \cdot 43,5^2 - 1,088 \cdot 156,72}}{0,544}}
\mathrm { x = \left\{ \begin{array}{ll} 129,29 \; cm \\ 4,46 \; cm \end{array} \right. }
Como o exemplo se trata de uma viga submetida à flexão simples (sem presença de esforços normais), não seria possível uma linha neutra que não cortasse a seção. Sendo assim, o resultado \mathrm{x = 129,29} \; cm pode ser descartado.
Cálculo da área de aço
Com a comprovação de que a linha neutra realmente corta a região da mesa (\mathrm{x = 4,46} \; cm), poderemos utilizar as formulações de dimensionamento de vigas retangulares, uma vez que, a região comprimida será retangular.
\mathrm{z = d - 0,4 \cdot = 53,5 - 0,4 \cdot 4,46}
\mathrm{z = 51,72 \; cm}
\mathrm{A_s = \dfrac{M_d}{z \cdot f_{yd}}}
\mathrm{A_s = \dfrac{30000}{51,72 \cdot 43,48}}
\mathrm{A_s = 13,34 \; cm^2}
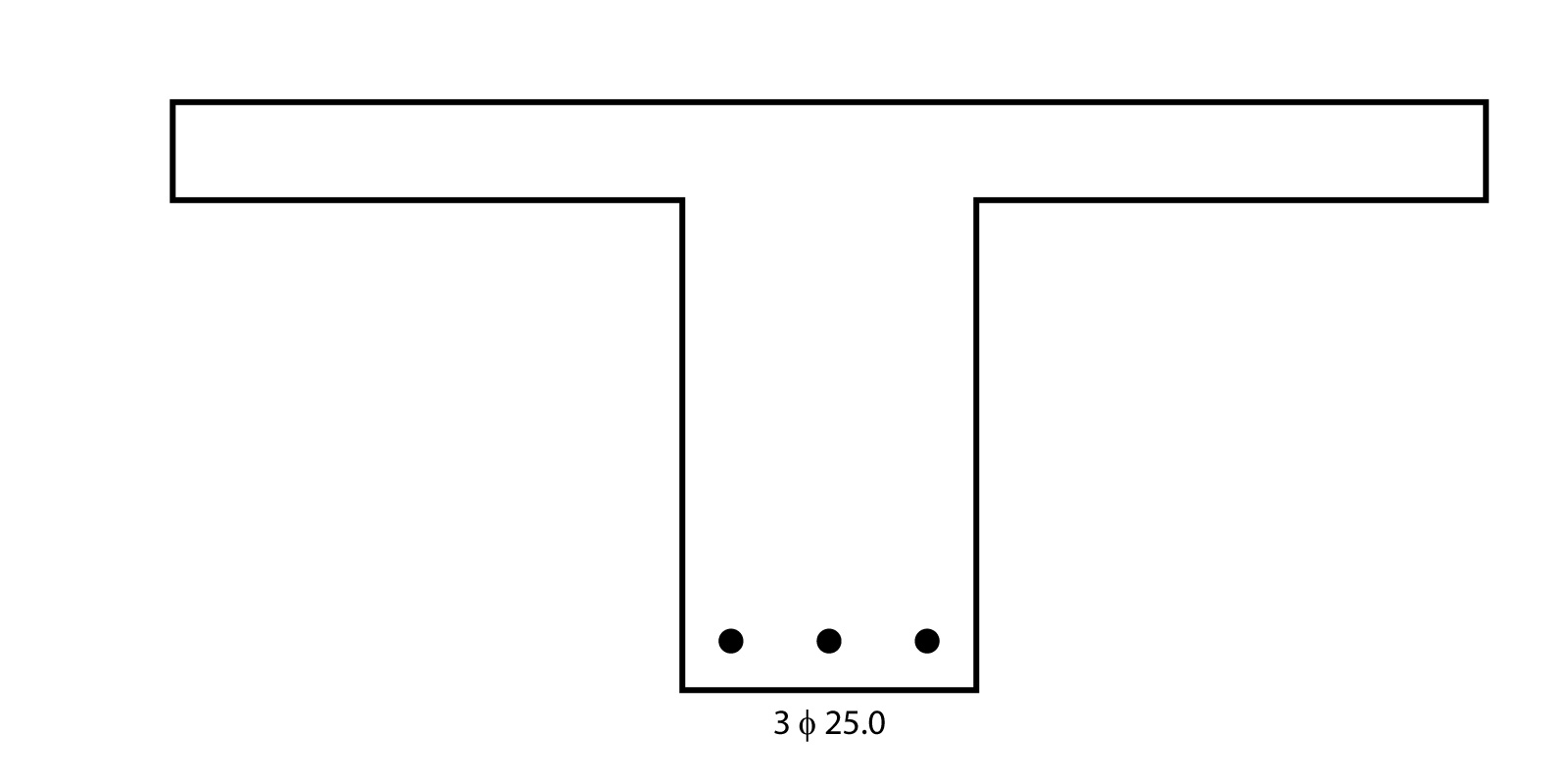
Dessa forma, conforme ilustra a figura abaixo, podemos utilizar 3 barras de 25 mm para resistir ao momento fletor solicitante.
Resolução por software de flexão simples:
Sabendo que o momento fletor de cálculo vale \mathrm{M_d = 30000 \; kN \cdot cm}:
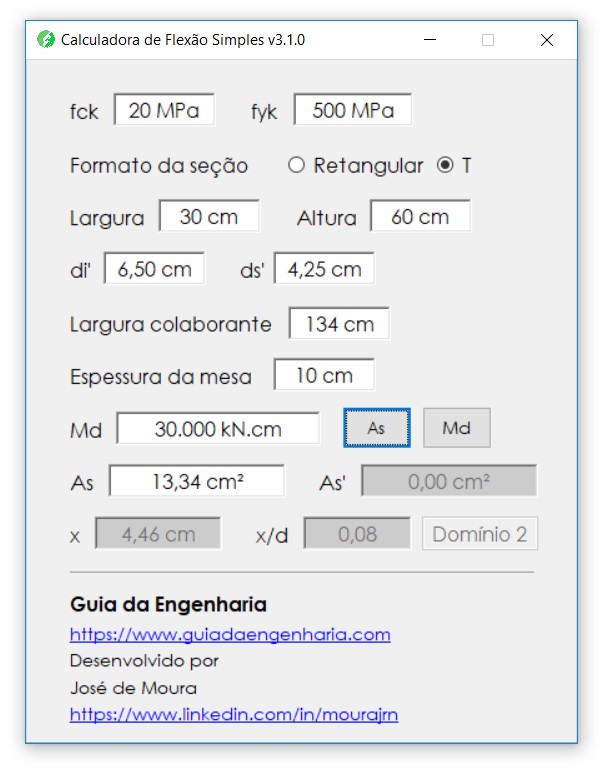
Como esperado, obtivemos os mesmos \mathrm{A_s = 13,34 \; cm^2} na parte inferior da viga utilizando a calculadora.
[formulario-calculadora-flexao]Segunda situação para a viga T
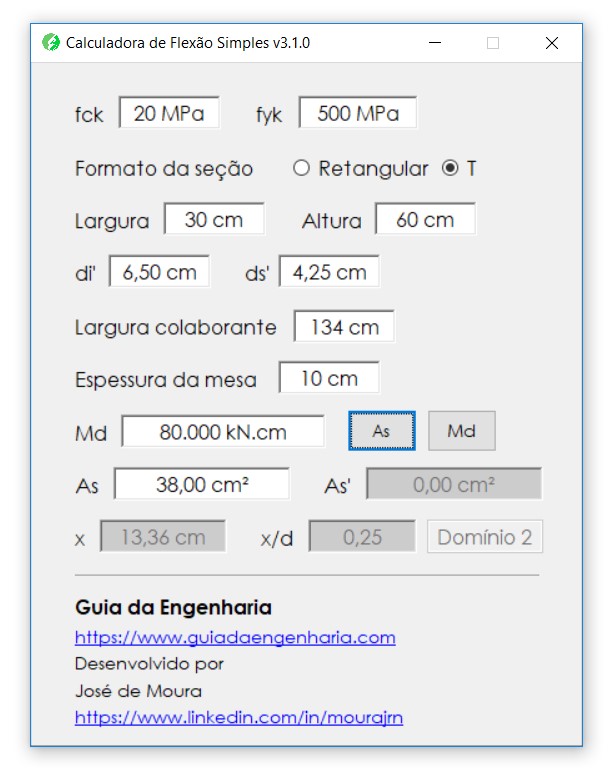
No segundo caso, vamos dimensionar a viga para um momento de cálculo máximo \mathrm{M_{Sd} = 80.000 \; kN \cdot cm}.
Cálculo da linha neutra
Considerando que a linha neutra irá cair dentro da mesa, vamos calcular a profundidade da mesma para uma largura igual a \mathrm{b_f}:
\mathrm{k=\dfrac{M_{Sd}}{b_f \cdot f_{cd}}}
\mathrm{k=\dfrac{80000}{134 \cdot \dfrac{2}{1,4}} = 417,91 \; cm^2}
\mathrm{x = \dfrac{0,68 \cdot d \pm \sqrt{0,4624 \cdot d^2 - 1,088 \cdot k}}{0,544}}
\mathrm{x = \dfrac{0,68 \cdot 53,5 \pm \sqrt{0,4624 \cdot 53,5^2 - 1,088 \cdot 417,91}}{0,544}}
\mathrm { x = \left\{ \begin{array}{ll} 121,06 \; cm \\ 12,69 \; cm \end{array} \right. }
Pelos mesmos motivos apontados para a situação anterior o resultado \mathrm{x = 121,06} \; cm pode ser descartado.
Momento resistido pelas abas
Dessa vez, a linha neutra não corta a mesa da viga, tornando incorreta nossa suposição inicial. A partir dessa constatação, iremos calcular o momento resistido apenas pelas abas:
\mathrm{M_1 = 0,85 \cdot f_{cd} \cdot \left( b_f - b_w \right) \cdot h_f \cdot \left(d - \dfrac{h_f}{2} \right)}
\mathrm{M_1 = 0,85 \cdot \dfrac{2}{1,4} \cdot \left( 134 - 30 \right) \cdot 10 \cdot \left(53,5 - \dfrac{10}{2} \right)}
\mathrm{M_1 = 61.249\; kN \cdot cm}
Momento resistido pela alma
O próximo passo é calcular o momento restante, que deverá ser resistido pela alma.
\mathrm{M_2 = M_{Sd} - M_1}
\mathrm{M_2 = 80000 - 61249 = 18.751 \; kN \cdot cm}
A partir do valor encontrado e considerando apenas a largura da alma podemos então obter a profundidade da linha neutra.
\mathrm{k=\dfrac{M_2}{b_w \cdot f_{cd}}}
\mathrm{k=\dfrac{18751}{30 \cdot \dfrac{2}{1,4}} = 437,52 \; cm^2}
\mathrm{x = \dfrac{0,68 \cdot d \pm \sqrt{0,4624 \cdot d^2 - 1,088 \cdot k}}{0,544}}
\mathrm{x = \dfrac{0,68 \cdot 53,5 \pm \sqrt{0,4624 \cdot 53,5^2 - 1,088 \cdot 437,52}}{0,544}}
\mathrm { x = \left\{ \begin{array}{ll} 120,39 \; cm \\ 13,36 \; cm \end{array} \right. }
Cálculo da área de aço
A única solução que satisfaz o problema em questão é \mathrm{x = 13,36} \; cm. A área de aço total é o somatório da área referente ao momento resistido pelas abas e a área referente ao momento resistido pela mesa.
\mathrm{A_s = A_{s1} + A_{s2}}
\mathrm{A_{s1} = \dfrac{M_1}{ \left(d - \dfrac{h_f}{2} \right) \cdot f_{yd}}}
\mathrm{A_{s1} = \dfrac{61249}{ \left(53,5 - \dfrac{10}{2} \right) \cdot 43,48}}
\mathrm{A_{s1} = 29,04 \; cm^2}
\mathrm{A_{s2} = \dfrac{M_2}{(d - 0,4 \cdot x) \cdot f_{yd}}}
\mathrm{A_{s2} = \dfrac{18751}{(53,5 - 0,4 \cdot 13,36) \cdot 43,48}}
\mathrm{A_{s2} = 8,96 \; cm^2}
\mathrm{A_s = 38 \; cm^2}
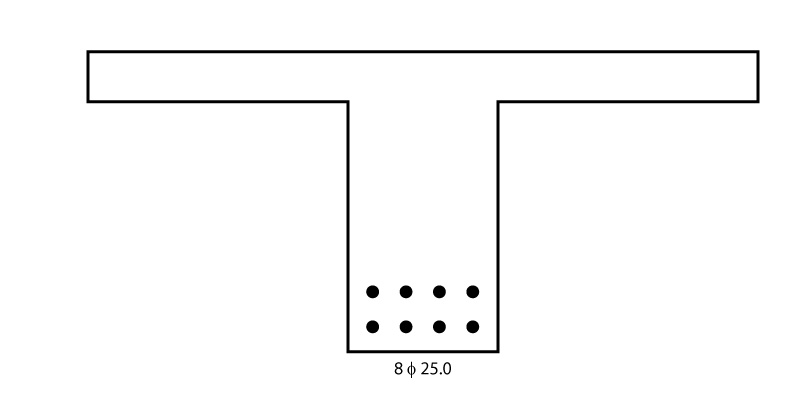
A figura abaixo apresenta uma solução para a área de aço necessária. Foram utilizadas 8 barras de 25 mm, obtendo uma área de aço efetiva de \mathrm{A_{s,ef} = 40 \; cm^2}.
Sabendo que o momento fletor de cálculo vale \mathrm{M_d = 80000 \; kN \cdot cm}:
Como esperado, obtivemos os mesmos \mathrm{A_s = 38 \; cm^2} na parte inferior da viga utilizando a calculadora.
Terceira situação para a viga T
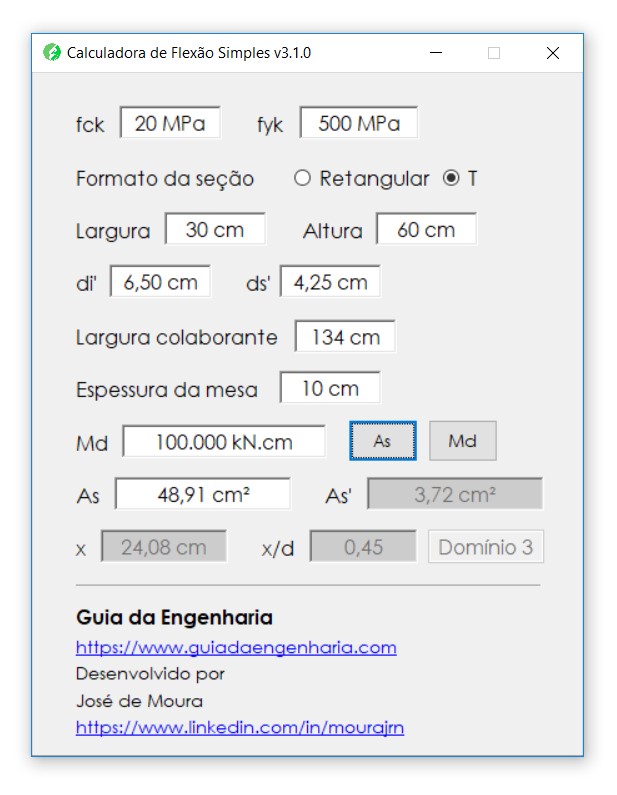
Para a última situação analisada, vamos considerar um momento máximo de cálculo de \mathrm{M_{Sd} = 100.000 \; kN \cdot cm}.
Como esse momento é superior ao momento do caso anterior, já temos a certeza que a linha neutra cortará a região da alma e por se tratar da mesma viga já sabemos também que o momento resistido apenas pelas abas vale \mathrm{M_1 = 61.249 \; kN \cdot cm}.
A partir desse momento e considerando apenas a largura da alma podemos obter a profundidade da linha neutra.
\mathrm{M_2 = M_{Sd} - M_1}
\mathrm{M_2 = 100000 - 61249 = 38.751 \; kN \cdot cm}
\mathrm{k=\dfrac{M_2}{b_w \cdot f_{cd}}}
\mathrm{k=\dfrac{38751}{30 \cdot \dfrac{2}{1,4}} = 904,19 \; cm^2}
\mathrm{x = \dfrac{0,68 \cdot d \pm \sqrt{0,4624 \cdot d^2 - 1,088 \cdot k}}{0,544}}
\mathrm{x = \dfrac{0,68 \cdot 53,5 \pm \sqrt{0,4624 \cdot 53,5^2 - 1,088 \cdot 904,19}}{0,544}}
\mathrm { x = \left\{ \begin{array}{ll} 100,76 \; cm \\ 32,99 \; cm \end{array} \right. }
Conforme comentado nas hipóteses de cálculo, para concretos de até 50 MPa e sem redistribuição de momentos o limite da profundidade da linha neutra vale \mathrm{\dfrac{x}{d} = 0,45 \therefore x = 24,08 \; cm}. Sendo assim, uma vez que encontramos uma profundidade de linha neutra superior ao limite, para garantir uma linha neutra aceitável deveremos utilizar armadura dupla, ou seja, adicionar aço na região comprimida da peça.
O momento restante deverá ser resistido pelo concreto na região da alma e por um binário de armaduras comprimidas e tracionadas.
Momento resistido pelas abas
Uma vez que já conhecemos o momento resistido pelas abas, vamos partir para o cálculo da armação responsável por resistir a esse momento.
\mathrm{A_{s1} = \dfrac{M_1}{ \left(d - \dfrac{h_f}{2} \right) \cdot f_{yd}}}
\mathrm{A_{s1} = \dfrac{61249}{ \left(53,5 - \dfrac{10}{2} \right) \cdot 43,48}}
\mathrm{A_{s1} = 29,04 cm^2}
Momento resistido pela alma
Podemos agora calcular o momento resistido pela alma (fixando a linha neutra no limite da norma) e a área de aço necessária para resisti-lo.
\mathrm{M_2 = 0,251 \cdot f_{cd} \cdot b_w \cdot d^2}
\mathrm{M_2 = 0,251 \cdot \dfrac{2}{1,4} \cdot 30 \cdot 53,5^2}
\mathrm{M_2 =30790 \; kN \cdot cm}
\mathrm{A_{s2} = \dfrac{M_2}{0,82 \cdot d \cdot f_{yd}}}
\mathrm{A_{s2} = \dfrac{30790}{0,82 \cdot 53,5 \cdot 43,48}}
\mathrm{A_{s2} = 16,14 \; cm^2}
Momento resistido pelo binário de armadura tracionada e comprimida
Vamos calcular agora o momento restante, que deve ser resistido por um binário formado por armadura tracionada e armadura comprimida.
\mathrm{M_3 = 100000 - M_1 - M_2}
\mathrm{M_3 = 75000 - 61249 - 30790}
\mathrm{M_3 = 7961 \; kN \cdot cm}
A área de aço para resistir a esse momento vale:
\mathrm{A_{s3} = \dfrac{M_3 }{(d - d') \cdot f_{yd}}}
\mathrm{A_{s3} = \dfrac{7961}{(53,5 - 4,25) \cdot 43,48}}
\mathrm{A_{s3} = 3,72 \; cm^2}
Cálculo da área de aço tracionado para a viga T
A área de aço total que deve ser adiciona a região inferior da viga é calculada pelo somatório das três áreas de aço anteriores.
\mathrm{A_s = A_{s1} + A_{s2} + A_{s3}}
\mathrm{A_s = 29,04 + 16,14 + 3,72}
\mathrm{A_s = 48,9 \; cm^2}
Cálculo da área de aço comprimido
Partindo agora para a área de aço comprimida, devemos primeiro verificar se a mesma está escoando. Para isso, vamos calcular a deformação específica dessas barras.
\mathrm{\epsilon_s ' = \dfrac{0,0035 \cdot (0,45 \cdot d - d')}{0,45 \cdot d}}
\mathrm{\epsilon_s ' = \dfrac{0,0035 \cdot (0,45 \cdot 53,5 - 4,25)}{0,45 \cdot 53,5}}
\mathrm{\epsilon_s ' = 2,88 \; ‰}
Como a deformação do aço comprimido é superior a deformação de escoamento (\mathrm{\epsilon_{yd} = 0,00207} para aço CA50), a tensão atuante no mesmo é igual a tensão de escoamento. Logo, a área de aço comprimida vale:
\mathrm{A_s ' = \dfrac{M_3}{(d - d') \cdot f_s '}}
\mathrm{A_s ' = \dfrac{7961}{(53,5 - 4,25) \cdot 43,48}}
\mathrm{A_s ' = 3,72 \; cm^2}
A fim de armar a viga em questão para as áreas de aço calculadas, foram utilizadas 10 barras de 25 mm na região tracionada da viga e 2 barras de 16 mm na região comprimida da mesma, conforme ilustrado abaixo.
Sabendo que o momento fletor de cálculo vale \mathrm{M_d = 100000 \; kN \cdot cm}:
Como esperado, obtivemos os mesmos \mathrm{A_s = 48,91 \; cm^2} na parte inferior da viga e \mathrm{A_s ' = 3,72 \; cm^2} na parte superior da viga utilizando a calculadora.
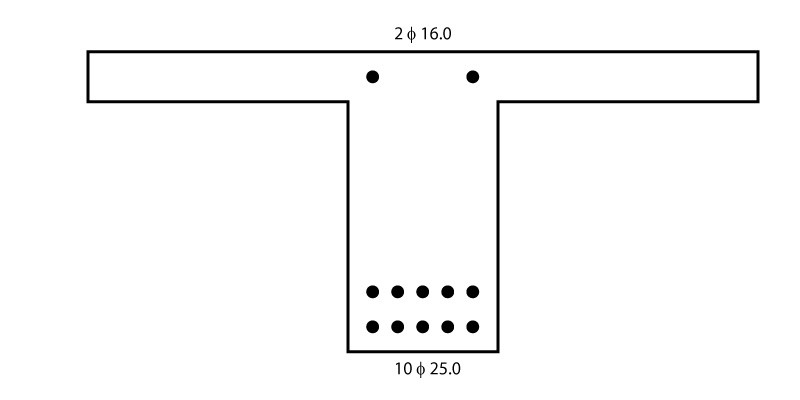
Nesse post você aprendeu, através de vários exemplos práticos, a dimensionar uma viga T de concreto armado submetida a momentos fletores variados. Se você gostou desse texto ou se ainda possui alguma dúvida, deixe uma mensagem nos comentários abaixo!
Até a próxima!
Fonte:
ARAÚJO, J. M. Curso de Concreto Armado. Rio Grande: Editora Dunas, 2014. v. 1
ASSOCIAÇÃO BRASILEIRA DE NORMAS TÉCNICAS. NBR 6118: Projeto de estruturas de concreto – Procedimento. Rio de Janeiro, 2014.
CARVALHO, R. C.; FIGUEIREDO FILHO, J. R. Cálculo e Detalhamento de Estruturas Usuais de Concreto Armado Segundo a NBR 6118:2014. São Carlos: EdUFSCar, 2014.
Gostaria de ter acesso a um curso sobre modelagem de alvenaria estrutural no Revit?
Aproveite enquanto está com um preço especial.
Obrigado…vou tentar
Me ajudou bastante
Obrigado pelo feedback, Salimo
Se surgir alguma dúvida deixa aqui nos comentários
olá, como é adotado a distância da fibra mais fracionada até o centro das armações? já que não é dabodp se haverá armadura dupla?
obrigado.
Olá, Marcelo,
Se estiver se referindo ao d’ superior, basta tirar o cobrimento e meio diâmetro estimado.
Como sei que seria necessário armadura dupla em um dos exemplo, coloquei logo.
Espero ter ajudado,
Abraços!