Condições de locomoção para equipamentos de terraplenagem

Quer descobrir quais equipamentos melhor se adequam a determinadas tarefas e tipos de terreno?

Pois, neste post, iremos estudar as condições de locomoção dos equipamentos de terraplenagem, mas não antes de conhecermos as forças que se opões ao movimentos desses equipamentos.

Ao fim, seremos capazes de determinar o esforço trator mínimo necessário para o equipamento de terraplenagem realizar as tarefas a que são destinados.

Vamos lá, então?

Resistências

Para iniciarmos nosso estudo, precisamos conhecer algumas das resistências opostas ao movimentos dos equipamentos. São elas:

Resistência ao rolamento

A resistência ao rolamento é uma força que se opõe ao rolamento das rodas pneumáticas de um equipamento e é oriunda dos atritos internos, que dependem tanto da deformação dos pneus como da penetração destes no solo.

Em outras palavras, a resistência ao rolamento é caracterizada como a menor força horizontal capaz de iniciar o movimento do equipamento e, em situações ideais, esse valor equivale a 2% do peso do equipamento.

O esquema abaixo exemplifica isso.

Desse modo, essa força de resistência , então, calculada por:

\mathrm{RRo=k.P}

Onde:

• RRo é a resistência ao rolamento (kgf);
• P é o peso total do equipamento (t);
• k é o coeficiente de rolamento (kgf/t), k=20+6.a ou tabela 1;
• a é o afundamento das rodas (cm).

Tabela 1 – Resistência média ao rolamento

Tipos de solos	k (kgf/t)
Estrada compactada, pavimento de concreto ou macadame betuminoso (não cede sob peso)	20
Estrada firme ou macadame hidráulico (cede levemente)	30 a 35
Estrada de terra estabilizada (penetração dos pneus de 25 a 50 mm)	50
Estrada de terra não estabilizada (penetração dos pneus de 10 a 15 cm)	75
Estrada de terra solta, arenosa, lamacenta ou sulcada e sem manutenção	100 a 200

Quando, no entanto, além do afundamento do solo houver também presença obstáculos no terreno, a resistência será também calculada por:

\mathrm{RRo_{obstáculo}=P\sqrt{\dfrac{h}{2R}}}

Onde:

• RRo é a resistência ao rolamento para equipamentos de roda (kgf);
• P é o peso do equipamento (t);
• h é a altura do obstáculo (cm);
• R é o raio do pneu (cm).

Resistência de rampa

A resistência de rampa se assemelha muito à resistência de rolamento, com a diferença de que a resistência ao movimento, neste caso, é provocada pelo peso do equipamento quando este está sobre um plano inclinado ascendente.

No entanto, quando este plano é descendente, ou seja, quando trata-se de um declive, ao invés de resistência ao rolamento temos uma assistência de rolamento. Desse modo, o movimento é, então, favorecido e a resistência adquire o valor negativo.

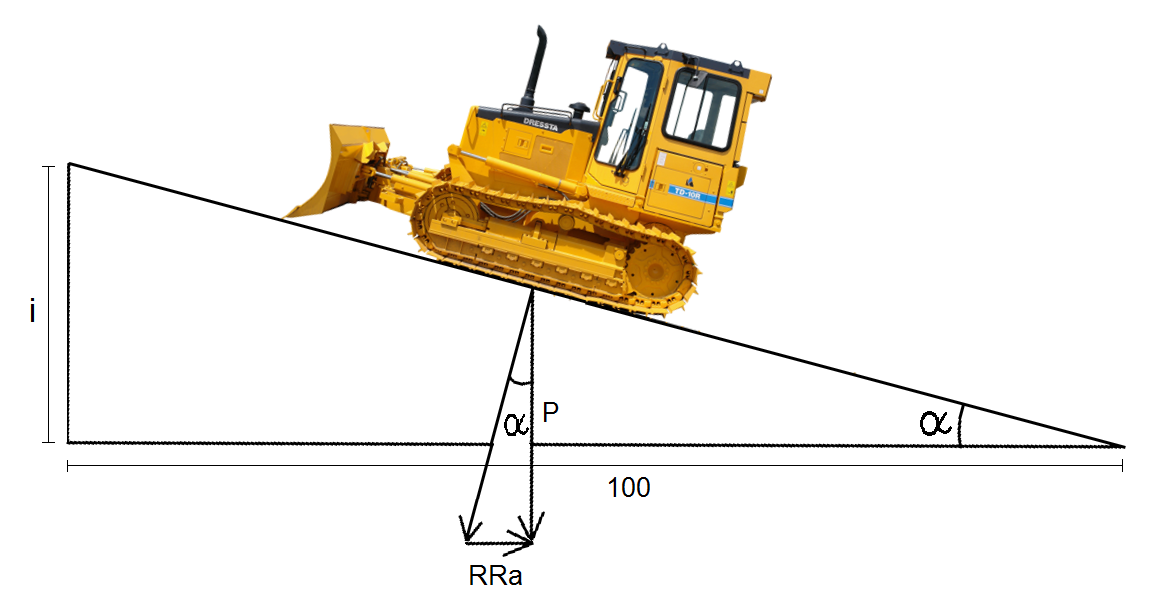
A resistência de rampa é calculado pela expressão abaixo:

\mathrm{RRa=P\cdot{senα}}

Para valores pequenos do ângulo α, podemos reescrever a expressão acima. Isso porque, nesta situação, senα = tgα = i/100. Logo, temos:

\mathrm{RRa=±P\cdot{i/100}}

Onde:

• RRa é a resistência de rampa (kgf), valor positivo para aclives e negativo para declives;
• P é o peso do equipamento (kgf);
• i é a inclinação (%).

Resistência a inércia

A resistência a inércia é derivada das leis de Newton e surge sempre quando um corpo necessita variar sua velocidade (Δv) em um dado intervalo de tempo (t).

Desse modo, quanto maior a massa do corpo, ou seja, quanto maior seu peso, maior essa resistência e ela se dá por:

 

\mathrm{Ri=±28,3\cdot\dfrac{P\cdotΔv}{t}}

Onde:

• Ri é a resistência à inércia (kgf), valor positivo para movimentos acelerados e negativo para movimentos desacelerados;
• P é o peso do equipamento (kgf);
• Δv é a variação de velocidade (m/s);
• t é o tempo (s).

Resistência ao ar

Por fim, a resistência do ar provém da pressão que o ar exerce sobre e seção transversal do equipamento em movimento e é calculada pela seguinte expressão:

\mathrm{Rar=\dfrac{k'\cdot{S}\cdot{v^2}}{13}}

Onde:

• Ri é a resistência ao ar (kgf);
• k’ é a constante, geralmente vale 0,07;
• S é a área da seção perpendicular a direção do movimento (m²);
• v é a velocidade (km/h).

 

Conhecidas as resistências ao movimentos, devemos somá-las para encontrar o valor total da resistência. Como isso, podemos determinar o esforço trator mínimo necessário ao equipamento, conforme as condições de movimento apresentadas a seguir.

Condições de movimento

A seguir, iremos apresentar as duas condições de movimento.

Primeiro, no entanto, precisamos entender como funciona o conjugado na roda do equipamento (Cr), constituinte das forças Er, iguais e opostas: no eixo da roda motriz que desloca sobre o terreno e na periferia do pneu, junto ao solo.

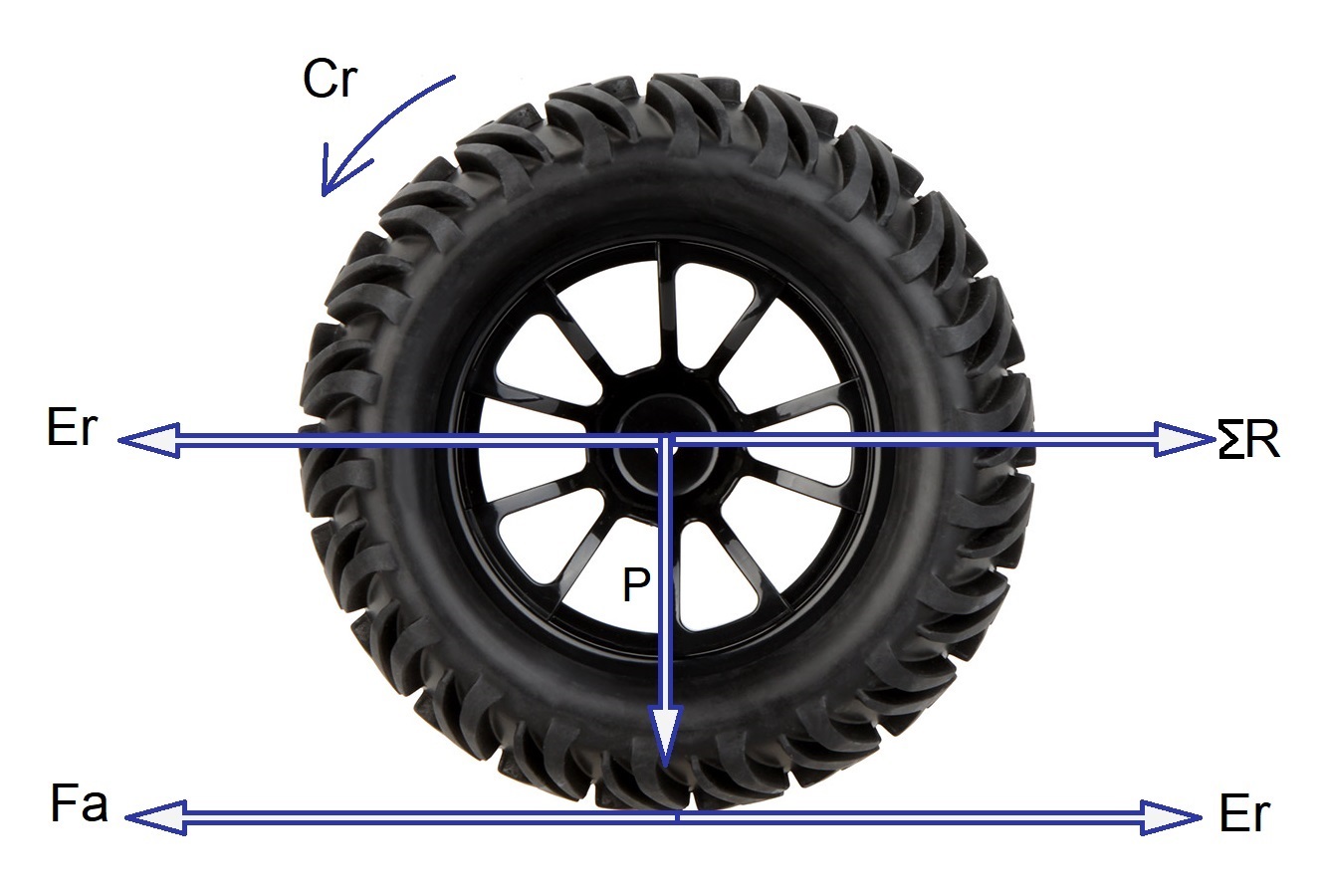
Esse conjugado é, então, calculado por:

\mathrm{Cr=Er\cdot{r}=Fa\cdot{r}}

• Cr é conjugado atuante na roda motriz ou torque (kgf.m);
• Er é o esforço trator atuante na roda motriz (kgf);
• r é o raio da roda motriz (m);
• Fa força de atrito necessária ao movimento (Kgf), Fa=f.Pm.
• f é o coeficiente de atrito, tabela 2.
• Pm é o peso sobre a roda motriz (kgf);
• ∑R é a soma das forças opostas ao movimento (kgf);

Tabela 2 – Coeficientes de atrito f

Tipo de superfície	Pneus	Esteiras
Pavimento de concreto	0,90	0,45
Terreno argiloso seco ou terra firme	0,55	0,90
Terra solta	0,45	0,60
Terra úmida firme	0,45	0,70
Areia seca	0,20	0,30
Areia úmida	0,40	0,50
Argila seca	0,55	0,90
Argila úmida	0,45	0,70
Cascalho	0,36	0,50
Pedra	0,65	0,55
Neve	0,20	0,25

Primeira condição

A primeira condição de movimento de uma máquina está intimidamente ligada à segunda lei de Newton e afirma que esse movimento somente é possível se o esforço trato for maior ou igual à soma das resistências.

Em outra palavras, só há movimento se a soma das forças for positiva:

ΣF ≥ 0

Er-ΣR ≥ 0

Er ≥ ΣR

Além disso, no caso de o equipamento estar parado, a condição inicial para que haja movimento é que, obrigatoriamente:

Er > ∑R

Já, se o equipamento já estiver em movimento, a condição para que ele continue em movimento uniforme é:

Er = ∑R

Resumidamente:

Tabela 3 – Primeira condição de movimento

Equipamento parado	Er>∑R	Há movimento
	Er=∑R	Há movimento
	Er<∑R	Não há movimento
Equipamento em movimento	Er>∑R	Movimento acelerado
	Er=∑R	Movimento uniforme
	Er<∑R	Movimento desacelerado

Segunda condição

Já segunda condição demovimento é um pouco mais específica e leva em consideração a força de aderência entre a roda e o terreno, que ocorre da seguinte forma:

Os valores crescentes de resistência ∑R exigem valores crescentes de esforço trator Er para que seja atendida a primeira condição.
Por se tratar de um binário, o crescimento do esforço trator Er implica no crescimento de igual valor do Er oposto a ele.
Desse modo, o valor de Er a cada instante é igual e diretamente oposto à força de atrito Fa. No entanto, a Fa não cresce indefinidamente e, em algum momento, pode ser excedida por Er. Quando isso ocorre, há patinação.

Desse modo, se Er ≥ Fa, ocorre patinação. Caso contrário, o equipamento rola sobre a superfície.

De maneira sintética:

Tabela 3 – Segunda condição de movimento

Equipamento parado	Er>∑R	Er<Fa	Há movimento
	Er>∑R	Er>Fa	Não há movimento, pois ocorre patinação
	Er>∑R	Er=Fa	Não há movimento, pois ocorre patinação
	Er=∑R	Er<Fa	Não há movimento
Equipamento em movimento	Er>∑R	Er<Fa	Há movimento acelerado
	Er>∑R	Er>Fa	Há movimento acelerado e patinação
	Er>∑R	Er=Fa	Há movimento acelerado e patinação
	Er=∑R	Er<Fa	Há movimento uniforme
	Er<∑R	Er<Fa	Há movimento desacelerado
	Er<∑R	Er>Fa	Há movimento desacelerado e patinação
	Er<∑R	Er=Fa	Há movimento desacelerado e patinação

 

Pois bem, essas foram algumas considerações sobre os equipamentos de terraplenagem, espero muito que esse post tenha sido útil pra você.

Se gostou, siga a gente aqui, no Youtube e também no Instagram!

Ah, e deixe comentários se tiver alguma dúvida.

A gente se vê num próximo post!

 

---

Fonte:

CAVALCANTE, Lucas. Produção dos equipamentos de terraplenagem. Quixadá: FCRS, 2018.

JAWORSKI, Tadeo. Equipamentos para escavação, compactação e transporte. Curitiba, 2011.

MEDEIROS, Rosinaldo. Métodos e equipamentos de construção. Roraima: UFRR, 2019.