Você sabia que a maioria das vigas em edifícios usuais de concreto armado podem ser dimensionadas como viga do formato de T? Pois é, isso se dá devido ao fato de que vigas e lajes não são elementos independentes e, de fato, trabalham em conjunto.
Nas próximas linhas você irá aprender como levar em consideração a interação entre vigas e lajes e como dimensionar uma viga T.
Nomenclaturas e variáveis de uma viga T
Antes de partimos para o equacionamento é importante nomearmos as variáveis e as regiões de uma viga de seção T:
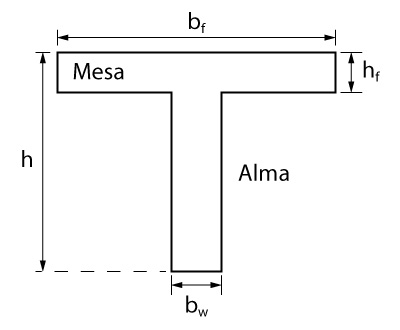
- Mesa: para os casos em que se trata de interação entre viga e laje, equivale a parcela da laje. Também é denominada de flange;
- Alma: para os casos em que se trata de interação entre viga e laje, equivale a própria viga. Também é denominada de nervura;
- \mathrm{b_f}: largura da mesa;
- \mathrm{b_w}: largura da alma;
- \mathrm{h_f}: espessura da mesa;
- \mathrm{h}: altura total da viga.
Largura colaborante de vigas de seção T
Uma vez que vigas e lajes trabalham de maneira monolítica, a tensão normal que surge na viga devido à flexão, não se limita a região da mesma, conforme ilustra a figura abaixo.
A norma brasileira ABNT/NBR: 6118 (2014) nos permite levar em consideração a ação entre viga e laje através da utilização de uma largura colaborante \mathrm{b_f}.
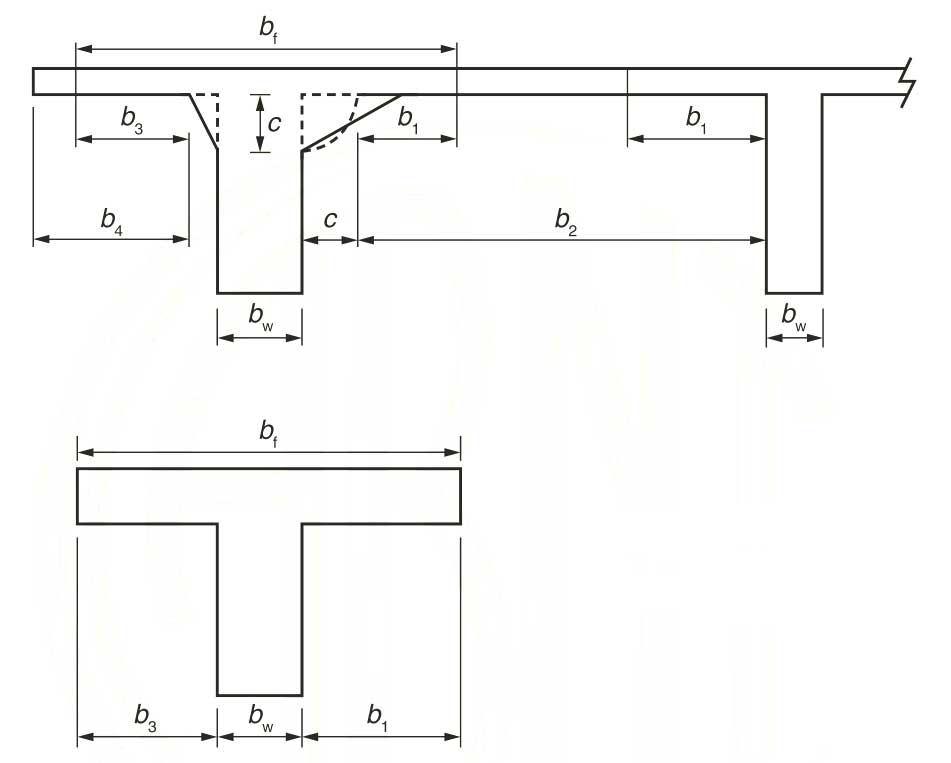
Sabendo que \mathrm{b_2} equivale a distância de face a face entre duas vigas e \mathrm{b_4} equivale a distância da face da viga ao fim da laje (caso não tenha outra viga nesse sentido), os valores \mathrm{b_1} e \mathrm{b_3} que devem ser acrescidos para cada lado, valem:
\mathrm { b_1 \leq \left\{ \begin{array}{ll} 0,5 \cdot b_2 \\ 0,1 \cdot a \end{array} \right. }
\mathrm { b_3 \leq \left\{ \begin{array}{ll} b_4 \\ 0,1 \cdot a \end{array} \right. }
A variável \mathrm{a} equivale a distância entre dois pontos de momento nulo e caso não seja calculada analisando o diagrama de momentos fletores, pode ser estimada em função do comprimento da viga:
a) viga simplesmente apoiada: \mathrm{a=1,00 \cdot l};
b) tramo com momento em uma só extremidade: \mathrm{a=0,75 \cdot l};
c) tramo com momentos nas duas extremidades: \mathrm{a=0,60 \cdot l};
d) tramo em balanço: \mathrm{a=2,00 \cdot l}.
Situações de cálculo de viga T
A diferença entre as formulações utilizadas no dimensionamento de vigas retangulares para uma viga T é que, caso a profundidade da linha neutra seja superior a espessura da mesa, a área comprimida não será mais uma região retangular.
Diante do exposto no parágrafo anterior, o primeiro passo no dimensionamento de um viga de seção T deve ser calcular a altura da linha para analisar se a mesma se encontra dentro da mesa da viga. Esse cálculo é realizado levando em conta uma seção retangular de largura \mathrm{b_f}.
O cálculo da linha pode ser realizado de acordo com a fórmula abaixo:
\mathrm{k=\dfrac{M_{Sd}}{b_f \cdot f_{cd}}}
\mathrm{x = \dfrac{0,68 \cdot d \pm \sqrt{0,4624 \cdot d^2 - 1,088 \cdot k}}{0,544}}
A partir desse cálculo teremos duas possibilidades: a linha neutra cair na mesa ou na alma na viga T.
Linha neutra na mesa da viga
Caso a linha neutra caia na mesa da viga, ou seja, \mathrm{x \leq h_f}, a região comprimida será retangular:
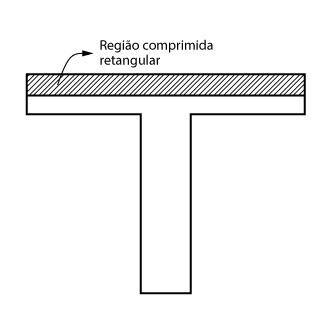
Nessa condição, o cálculo da área de aço será realizado de maneira idêntica a uma viga retangular de largura \mathrm{b_f}.
Linha neutra na alma da viga sem armadura dupla
Caso a linha neutra caia na alma, ou seja, caso \mathrm{x > h_f}, a região comprimida terá um formato de T.
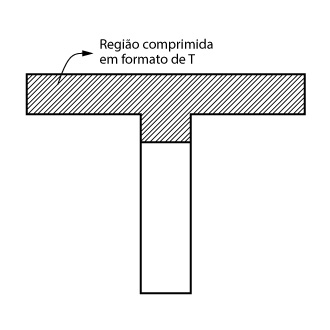
Dessa forma, dividiremos o momento solicitante em duas parcelas: a primeira, \mathrm{M_1}, resistida pelas duas abas da mesa e a segunda parcela, \mathrm{M_2}, resistida pela alma. Para cada uma dessas parcelas serão calculadas as áreas de aço necessárias.
Primeira parcela: compressão nas abas
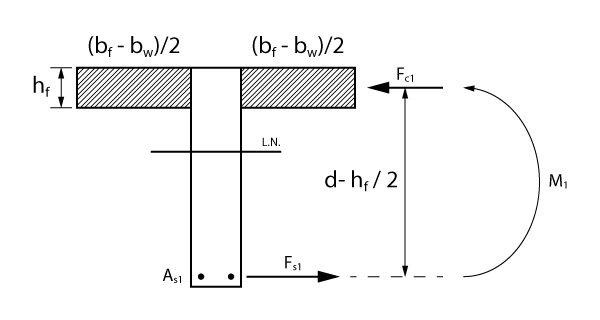
Para a primeira parcela, a área comprimida vale \mathrm{A_{c1} = 2 \cdot \left(\dfrac{b_f - b_w}{2}\right) \cdot h_f}. A força atuante nessa região é calculada apenas multiplicando essa área pela tensão atuante:
\mathrm{F_{c1} = 0,85 \cdot f_{cd} \cdot \left( b_f - b_w \right) \cdot h_f}
Agora basta multiplicarmos pelo braço de alavanca (que vale a distância entre o centro de compressão e as barras de aço) para obtermos o momento resistente \mathrm{M_1}:
\mathrm{M_1 = F_{c1} \cdot z_1}
\mathrm{M_1 = 0,85 \cdot f_{cd} \cdot \left( b_f - b_w \right) \cdot h_f \cdot \left(d - \dfrac{h_f}{2} \right)}
Segunda parcela: compressão na alma
O momento restante, \mathrm{M_2}, deverá ser resistido pela alma da viga:
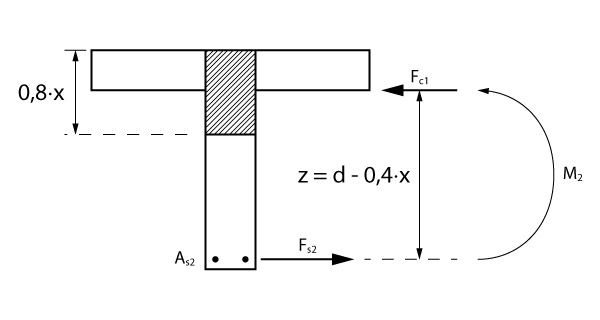
\mathrm{M_2 = M_{Sd} - M_1}
Em posse do momento que deve ser resistido pela alma, o próximo passo é calcular a profundidade da linha neutra real. Essa será calculada pela equação abaixo:
\mathrm{k=\dfrac{M_2}{b_w \cdot f_{cd}}}
\mathrm{x = \dfrac{0,68 \cdot d \pm \sqrt{0,4624 \cdot d^2 - 1,088 \cdot k}}{0,544}}
Repare que já utilizamos essa equação nesse post, as únicas alterações que fizemos foi a utilização de \mathrm{M_2} e \mathrm{b_w}. Basicamente o que estamos calculando é a altura da região de concreto comprimida em uma largura \mathrm{b_w} para resistir a um momento \mathrm{M_2}.
Cálculo da área de aço
Por fim, a área de aço total será o somatório das duas áreas de aço:
\mathrm{A_s = A_{s1} + A_{s2}}
\mathrm{A_s = \dfrac{M_1}{ \left(d - \dfrac{h_f}{2} \right) \cdot f_{yd}} + \dfrac{M_2}{(d - 0,4 \cdot x) \cdot f_{yd}}}
Observe que, essas duas parcelas de áreas de aço foram calculadas considerando as barras escoando. Lembre-se que de acordo com as hipóteses de cálculo a linha neutra é limitada de forma que seja garantido a ductilidade da peça. Dessa forma, o escoamento das barras inferiores é garantido.
Linha neutra na alma com armadura dupla
Caso o cálculo realizado acima resulte em uma linha neutra superior aos valores permitidos por norma (apenas como exemplo, para concretos de até 50 MPa sem distribuição de momentos, o limite vale \mathrm{x = 0,45 \cdot d}), o dimensionamento da viga é realizado com armadura dupla, ou seja, adicionando armação comprimida.
Assim como realizado para armadura dupla em vigas retangulares, o momento também será dividido em parcelas, mas com alguns detalhes a mais. A primeira parcela já foi explicada anteriormente, será o momento resistente apenas pelas abas. A parcela resistida pela alma será dividida em duas, uma parte resistida com a linha neutra fixada no limite de norma e o outra parte equivalente ao restante do momento, em que a compressão será resistida por uma armadura comprimida.
Primeira parcela: compressão nas abas
Então vamos formular o explicado no parágrafo anterior. A primeira parcela, já comentada, vale:
\mathrm{M_1 = 0,85 \cdot f_{cd} \cdot \left( b_f - b_w \right) \cdot h_f \cdot \left(d - \dfrac{h_f}{2} \right)}
Segunda parcela: compressão na alma
A segunda parcela, é apresentada na figura abaixo:
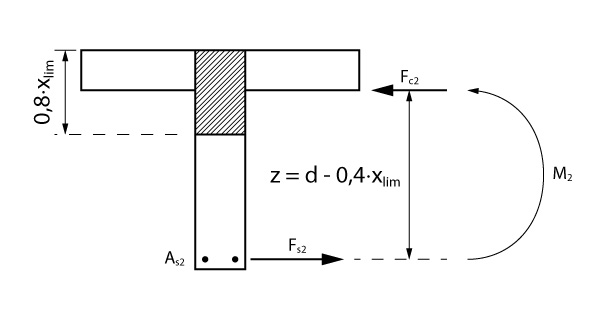
Vamos calcular o momento resistido pela aba igualando o mesmo ao gerado pelo binário apresentado na figura.
\mathrm{M_2 = F_{c2} \cdot (d - 0,4 \cdot x_{lim})}
\mathrm{M_2 = F_{c2} \cdot (d - 0,4 \cdot (0,45 \cdot d))}
\mathrm{M_2 = 0,85 \cdot f_{cd} \cdot b_w \cdot 0,8 \cdot x_{lim} \cdot 0,82 \cdot d}
\mathrm{M_2 = 0,85 \cdot f_{cd} \cdot b_w \cdot 0,8 \cdot 0,45 \cdot d \cdot 0,82 \cdot d}
\mathrm{M_2 = 0,251 \cdot f_{cd} \cdot b_w \cdot d^2}
Agora que o momento foi calculado, podemos obter a área de aço necessária para essa parcela:
\mathrm{M_2 = F_{s2} \cdot (d - 0,4 \cdot x_{lim})}
\mathrm{M_2 = F_{s2} \cdot (d - 0,4 \cdot (0,45 \cdot d))}
\mathrm{M_2 = F_{s2} \cdot 0,82 \cdot d}
\mathrm{M_2 = A_{s2} \cdot f_{yd} \cdot 0,82 \cdot d}
\mathrm{A_{s2} = \dfrac{M_2}{0,82 \cdot d \cdot f_{yd}}}
Terceira parcela: restante do momento com compressão na armadura comprimida
A última parcela, ilustrada na figura abaixo, é resistida pelo binário gerado pela armadura tracionada, \mathrm{A_{s3}}, e a armadura comprimida \mathrm{A_s '}.
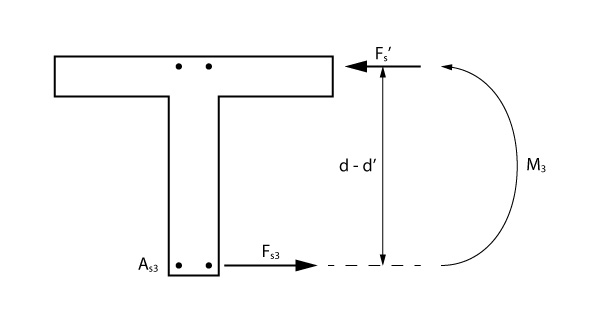
O valor da parcela \mathrm{M_3} representa o restante do momento solicitante de cálculo:
\mathrm{M_3 = M_{Sd} - M_1 - M_2}
Armadura tracionada
Podemos então, calcular a armadura de tração para resistir a esse momento:
\mathrm{M_3 = F_{s3} \cdot (d - d')}
\mathrm{M_3 = A_{s3} \cdot f_{yd} \cdot (d - d')}
\mathrm{A_{s3} = \dfrac{M_3 }{(d - d') \cdot f_{yd}}}
Repare que novamente calculamos a armadura inferior com a tensão igual a tensão de escoamento. Isso é garantido por termos a certeza, uma vez que limitamos profundidade da linha neutra, que a seção se encontra no domínio 3.
Armadura comprimida
Conforme comentando para armadura dupla de vigas retangulares, não temos a garantia que a armadura comprimida esteja escoando. Sabendo que o para o domínio 3 o encurtamento no concreto vale 3,5 ‰, é possível calcular a deformação na armadura comprimida:
\mathrm{\epsilon_s ' = \dfrac{0,0035 \cdot (x_{lim} - d')}{x_{lim}}}
\mathrm{\epsilon_s ' = \dfrac{0,0035 \cdot (0,45 \cdot d - d')}{0,45 \cdot d}}
Com a deformação calculada o próximo passo é obter a tensão atuante da armadura:
\mathrm { f_s ' = \left\{ \begin{array}{ll} 21.000 kN/cm^2 \cdot \epsilon_s '; se \epsilon_s ' < \epsilon_{yd} \\ f_{yd}; se \epsilon_s ' \geq \epsilon_{yd} \end{array} \right. }
Por fim, a armação adicionada na região comprimida vale:
\mathrm{A_s ' = \dfrac{M_3}{(d - d') \cdot f_s '}}
Resumo da área de aço
Para a região tracionada da viga será adicionada a área de aço equivalente ao somatório das três áreas abaixo:
\mathrm{A_s = A_{s1} + A_{s2} + A_{s3}}
E para a região comprimida da viga será adicionada a área de aço \mathrm{A_s '}.
Parabéns por ter chegado até aqui! Agora que você já está afiado na teoria, o próximo passo é avançar para a resolução de exercícios a fim de fixar os conteúdos aprendidos. Dúvidas e sugestões são sempre bem vindos nos comentários abaixo.
Até a próxima!
Fonte:
ARAÚJO, J. M. Curso de Concreto Armado. Rio Grande: Editora Dunas, 2014. v. 1
ASSOCIAÇÃO BRASILEIRA DE NORMAS TÉCNICAS. NBR 6118: Projeto de estruturas de concreto – Procedimento. Rio de Janeiro, 2014.
CARVALHO, R. C.; FIGUEIREDO FILHO, J. R. Cálculo e Detalhamento de Estruturas Usuais de Concreto Armado Segundo a NBR 6118:2014. São Carlos: EdUFSCar, 2014.
Gostaria de ter acesso a um curso sobre modelagem de alvenaria estrutural no Revit?
Aproveite enquanto está com um preço especial.

Gostei muito do desenvolvimento teórico, mas penso que deveria vir acompanhado de exemplos práticos para facilitar o entendimento de alunos de graduação.
Muito obrigado pelo comentário, Sebastião!
No post eu coloquei um link para um post de exercícios:
https://www.guiadaengenharia.com/dimensionamento-viga-t-exemplos/
Grande abraço!
Olá, gostaria de usar a imagem dessas vigas no meu perfil profissional de engenharia no Instagram!
Seria possível?
Olá, Nicolly,
Espero que esteja tudo tranquilo contigo
Basta marcar nosso Instagram como fonte
Abraço