Uma das soluções muito utilizadas para lajes são as lajes nervuradas, que consistem basicamente em dispor o concreto formando nervuras ao invés de utilizar um maciço sólido, como em lajes maciças.
Nesse post você irá aprender como dimensionar de lajes nervuradas unidirecionais e também a selecionar a treliça comercial e as armações complementares.
Entre essas lajes podemos destacar duas soluções muito utilizadas em edificações de pequeno porte: lajes treliçadas e lajes com vigotas pré-moldadas. Conforme ilustra a figura abaixo, a diferença entra as duas opção é que na laje treliçada apenas a base da mesma é pré-fabricada.

Você pode conferir abaixo um modelo 3d de uma laje nervurada:
Ações nas lajes nervuradas
As ações usuais que atuam em lajes nervuradas são as cargas de revestimento, de peso do concreto, peso do enchimento, cargas acidentais (também denominadas de sobrecarga de utilização) e eventuais paredes sobre a laje.
Peso próprio
O peso próprio pode ser obtido apenas calculando a área de concreto da seção T formada por uma nervura e multiplicando pelo peso específico do concreto armado.
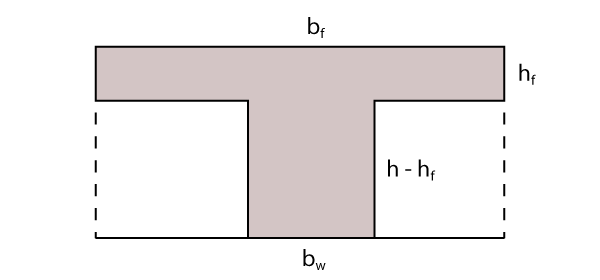
Dessa forma, a área de região T pode ser calculada pela equação abaixo:
\mathrm{A_c = b_w \cdot (h - h_f) + b_f \cdot h_f}
Em posse agora da área de concreto, podemos calcular o peso dessa região de nervura apenas multiplicando a área pelo peso específico:
\mathrm{g_1 = A_c \cdot \gamma}
Essa formulação já irá no fornecer o peso de concreto distribuído linearmente, que é como iremos inserir em nosso modelo.
Na realidade, o que é colocado como \mathrm{b_f} é a distância entre o eixo de duas nervuras adjacentes. Entretanto, para o caso de lajes nervuradas na analise de uma viga t, usualmente tem-se a largura útil (\mathrm{b_f}) igual à distância entre os eixos.
Revestimento
O peso do revestimento irá variar basicamente do material solicitado no projeto de arquitetura. Você pode conferir alguns pesos de materiais dentro na norma brasileira de ações ABNT/NBR: 6120 (2019).
Valores usuais de revestimento estão por volta de 0,8 kN/m² e 1,2 kN/m², podendo ser utilizada a média dos dois valores: 1,0 kN/m².
A fim de obter o valor de revestimento em cada nervura, basta multiplicarmos o valor por unidade de área pela distância entre eixos de duas nervuras.
Sobrecarga de utilização
As sobrecargas de utilização a serem distribuídas nas lajes podem ser obtidas na norma ABNT/NBR: 6120 (2019). A tabela a seguir apresenta as cargas acidentais distribuída por área em vários locais de um edifício residencial.
| Local | kN/m² |
| Dormitórios | 1.5 |
| Sala, copa, cozinha | 1.5 |
| Sanitários | 1.5 |
| Despensa, área de serviço e lavanderia | 2.0 |
| Quadras esportivas | 5.0 |
| Salão de festas, salão de jogos | 3.0 |
| Áreas de uso comum | 3.0 |
| Academia | 3.0 |
| Forro acessíveis apenas para manutenção e sem estoque de materiais | 0.1 |
| Sótão | 2.0 |
| Corredores dentro de unidades autônomas | 1.5 |
| Corredores de uso comum | 3.0 |
| Depósitos | 3.0 |
Novamente, para converter uma carga distribuída por área para uma carga distribuída linearmente basta multiplicarmos o valor pela distância entre eixos das nervuras.
Paredes diretamente sobre a laje
Primeiramente gostaria de destacar que existem outras verificações (exemplos: deslocamentos excessivos e cisalhamento) a serem feitos além do dimensionamento da armadura.
Dito isso, eu recomendo um cuidado extra ao dispor paredes diretamente sobre lajes unidirecionais.
As paredes podem estar dispostas basicamente em duas situações: paralelas à direção das nervuras e perpendiculares cruzando várias nervuras.
Para a primeira situação, devemos distribuir o carregamento da alvenaria como carregamento uniformemente distribuído na nervura correspondente.
Para a segunda situação, vamos aplicar o carregamento da parede como uma carga pontual na posição em que a parede cruza a nervura.
Dimensionamento à flexão
O projeto de estruturas de concreto armado, segundo a norma brasileira ABNT/NBR: 6118 (2014), baseia-se no método dos estados limites. Sendo que o cálculo da armação deve ser feito de acordo com o estado limite último normal.
Uma vez que essas lajes normalmente estão solicitadas apenas por um carregamento variável, que é a carga acidental, a combinação a ser verificada é basicamente o somatório das ações majoradas por 1,4.
Modelo de cálculo
Para o dimensionamento de lajes nervuradas unidirecionais usualmente são utilizados modelos em que as mesmas são consideradas como um conjunto de vigas trabalhando de forma independente, desprezando portanto a rigidez na direção transversal oferecida pela capa de concreto.
Se você tem interesse em ingressar na área de cálculo estrutural, recomendo bastante o curso Essencial em Concreto Armado do professor Rangel Lages em que você irá aprender a utilizar o software TQS (na minha opinião, o melhor software do mercado) passando por TODAS as etapas (desde a concepção estrutural até elaboração das pranchas) necessárias para o desenvolvimento de um projeto completo.
Levando em consideração que as nervuras são basicamente vigas isoladas e que usualmente essas nervuras estão submetidas a carregamentos uniformemente distribuídos ao longo de todo comprimento, podemos calcular o momento máximo pela seguinte equação:
\mathrm{M_{Sk} = \dfrac{q \cdot L^2}{8}}
Condições para lajes nervuradas
De acordo com a distância entre eixos e a largura da nervura a norma ABNT/NBR: 6118 (2014) define se devemos ou não verificar a flexão da mesa entre nervuras e como devemos verificar o cisalhamento das nervuras. Em algumas situações, o cisalhamento nas nervuras será verificado como viga e em outras, será verificado como laje.
Para melhorar seu entendimento, preparei um fluxograma que resume as condições presentes na norma:
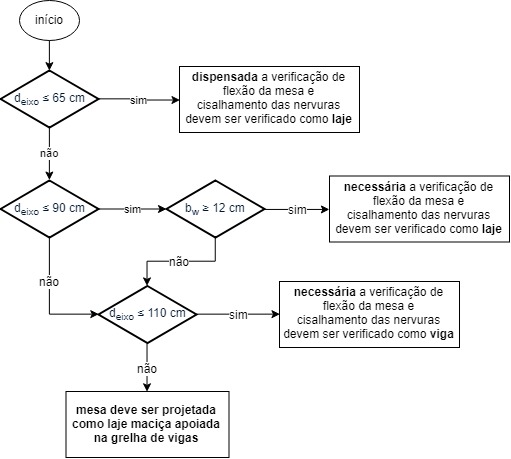
Conforme apresenta o diagrama, para situações em que a distância entre eixos das nervuras for inferior a 65 cm, não é necessário a verificação da flexão da mesa e o cisalhamento das nervuras deve ser verificado como laje.
Exemplo aplicado
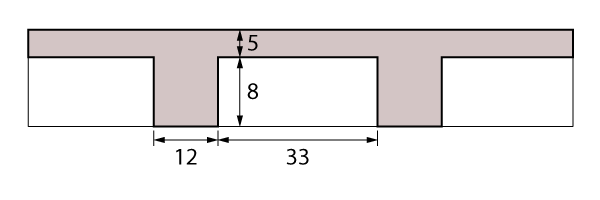
Como exemplo, será dimensionada uma laje com enchimento de 33 cm de largura por 8 cm de altura, nervura com 12 cm de largura e espessura da capa de 5 cm. O vão entre eixos de apoio vencido pela laje é de 3,0 m e seu uso é residencial. A Classe de Agressividade Ambiental da região foi considerada I, resultando em uma resistência característica do concreto mínima de 20 MPa (valor utilizado) e um cobrimento mínimo para lajes de 2,0 cm.
Caso você prefira, vou colocar a resolução de uma questão similar no vídeo abaixo.
Nesse dimensionamento, a carga de revestimento será considerada de 1 kN/m² e a carga acidental (sobrecarga de utilização) será considerada de 1,5 kN/m² (representando por exemplo um quarto). Além dessas cargas deve-se levar em conta o peso do concreto e o peso do enchimento.
Carregamentos distribuídos em cada nervura
No caso das cargas que já estão distribuídas na área (como o caso da sobrecarga de utilização e o revestimento) basta multiplicar as mesmas pela largura de influência de cada nervura. Este valor, conforme comentado anteriormente, é a distância entre eixos de duas nervuras.
Dessa forma, a carga acidental distribuída linearmente na nervura será:
\mathrm{0,45\cdot1,5=0,675\;kN/m}
De maneira análoga, o peso do revestimento distribuído linearmente pode ser calculado pela equação abaixo:
\mathrm{0,45\cdot1,0=0,45\;kN/m}
O peso próprio do concreto é levado em conta calculando a área de concreto suportada por cada nervura multiplicada pelo peso específico do concreto armado:
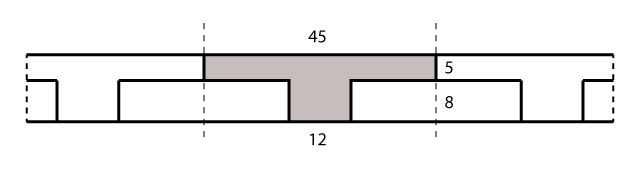
Na figura acima as medidas apresentadas estão em centímetro. Calculando a área de concreto resistido pela nervura:
\mathrm{0,45\cdot0,05+0,08\cdot0,12=0,0123\;m^2}
Sabendo que o peso específico do concreto armado é 25 kN/m³:
\mathrm{0,0123\cdot25=0,3075\;kN/m}
Para a laje em questão será considerado um enchimento em lajota cerâmica de peso específico de 18 kN/m³:
\mathrm{0,33\cdot0,08\cdot18=0,4752\;kN/m}
Momento fletor solicitante
Usualmente as lajes nervuradas unidirecionais são consideradas sem continuidade, ou seja, não existe uma restrição a rotação nos apoios. Levando isso em consideração e sabendo que nesse exemplo existem apenas carregamentos distribuídos ao longo de todo o vão, o momento fletor máximo ocorre no meio do vão e pode ser calculado pela seguinte equação:
\mathrm{M_{Sk}=\dfrac{q\cdot l^2}{8}}
Sabendo que o carregamento é o somatório das cargas atuantes na nervura:
\mathrm{q=0,675+0,45+0,3075+0,4752}
\mathrm{q=1,9077\;kN/m}
\mathrm{M_{Sk}=\dfrac{1,9077\cdot 3^2}{8}=2,146\;kN\cdot m}
O momento solicitante de cálculo é obtido, conforme citado anteriormente, multiplicando o valor característico por 1,4. Logo:
\mathrm{M_{Sd} = M_{Sk} \cdot 1,4 = 3,0 \; kN \cdot m}
Cálculo da altura útil
Sabendo que a altura útil é a distância do centro de gravidade da armadura tracionada até a borda comprimida e que a laje possui 13 cm de altura (8 cm do enchimento mais 5 cm de espessura de capa), cobrimento igual a 2 cm e admitindo inicialmente uma armação de 10 mm de diâmetro podemos calcular:
\mathrm{d = h - c - \dfrac{\phi}{2} = 13 - 2 - \dfrac{1}{2} = 10,5 \; cm}
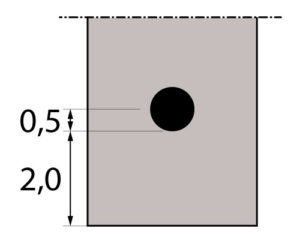
Profundidade da linha neutra
O cálculo da área de aço para lajes nervuradas é similar ao dimensionamento de uma viga em formato de T.
Partiremos da hipótese que a linha neutra esteja dentro de mesa de concreto. Dessa forma, iremos calcular inicialmente a profundidade da linha neutra para uma largura colaborante de 45 cm. Para isso, utilizaremos a tabela de KMD de Carvalho e Figueiredo Filho (2014).
\mathrm{KMD = \dfrac{M_{Sd}}{b_w \cdot d^2 \cdot f_{cd}}}
\mathrm{KMD= \dfrac{300}{45 \cdot 10,5^2 \cdot \dfrac{2}{1,4}}}
\mathrm{KMD=0,042 \rightarrow 0,05}
Considerando um KMD de 0,05, obtêm-se um KX de 0,0758 e um KZ de 0,9697.
\mathrm{x = KX \cdot d}
\mathrm{x = 0,0758 \cdot 10,5 = 0,8 \; cm}
Como altura da linha neutra calculada (0,8 cm) foi inferior a espessura da capa (5 cm), logo a hipótese de cálculo como seção retangular (consideração da largura igual a largura colaborante) está correta.
Cálculo da área de aço
Calculando então a área de aço:
\mathrm{A_s = \dfrac{M_d}{KZ \cdot d \cdot f_{yd}}}
\mathrm{A_s = \dfrac{300}{0,9697 \cdot 10,5 \cdot \dfrac{60}{1,15}}=0,57 \; cm^2}
Resolução por software de flexão simples:
Sabendo que o momento fletor de cálculo vale:
\mathrm{M_d = 300 \; kN \cdot cm}
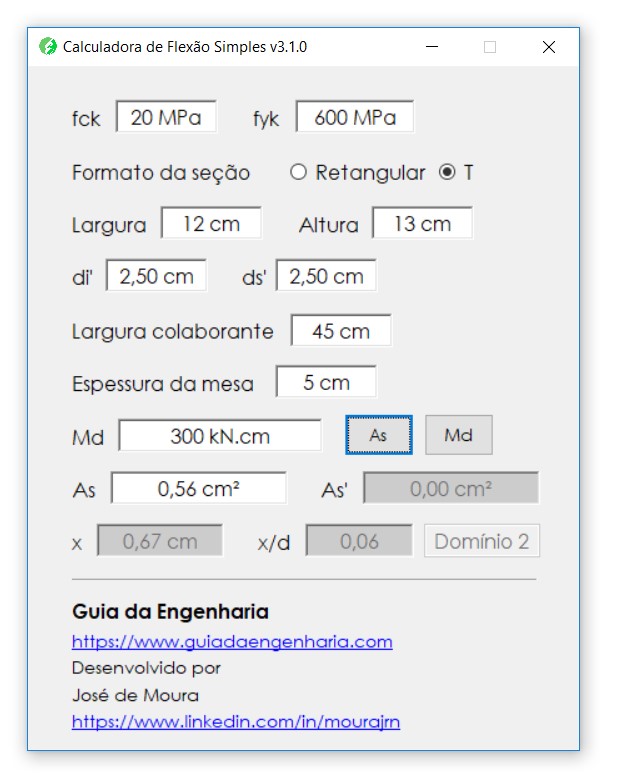
No caso, obtivemos uma área de aço \mathrm{As = 0,56 \; cm^2}, bem próxima da calculada manualmente.
Caso tenha interesse em conferir nossa Calculadora de Flexão Simples basta preencher o formulário abaixo:
[formulario-calculadora-flexao]Escolha da treliça
A partir de uma tabela de treliças comerciais, vamos escolher a treliça que forneceria uma área de aço igual ou superior a 0,57 cm².
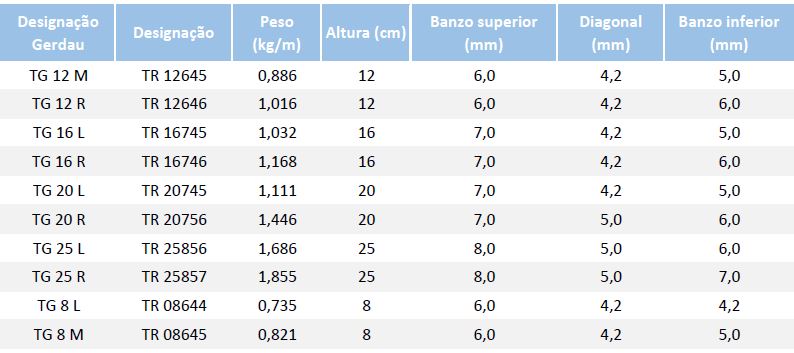
Considerando que a treliça TR 08645 possui dois fios de 5,0 mm no banzo inferior (0,4 cm²), a mesma só poderia ser utilizada com a utilização de barras complementares. No caso, poderia ser utilizada a treliça acima com a adição de um fio de 5,0 mm, totalizando um área de 0,6 cm² de aço CA60.
Armadura complementar de aço CA50
Caso houvesse a necessidade de utilizar aço CA50 como armadura complementar, inicialmente calcularíamos a força necessária para o equilíbrio. Sabendo que é necessário uma área 0,57 cm² de aço CA60, podemos encontrar a força necessária pela equação abaixo:
\mathrm{F_s = A_s \cdot f_{yd}=0,57 \cdot \dfrac{60}{1,15}}
\mathrm{F_s =29,74 \; kN}
Dos 29,74 kN necessários removeríamos a parcela que a treliça utilizada (TR 08645) já resiste:
\mathrm{29,74 - F_{_{CA60}}}
\mathrm{29,74 - 2 \cdot 0,2 \cdot \dfrac {60} {1,15} = 8,87 \; kN}
E calcularíamos então a área de aço de CA50 necessária para resistir uma força de 8,87 kN:
\mathrm{A_{s_{CA50}} \cdot \dfrac{50}{1,15} \geq 8,87 \; cm^2}
\mathrm{A_{s_{CA50}} = 0,2 \; cm^2}
Para o exemplo, seria possível adicionar uma barra CA50 de 6,3 mm.
Escolha da solução
A figura abaixo apresenta um detalhe da primeira solução fornecida: treliça TR 08645 com um fio de 5,0 mm complementar.
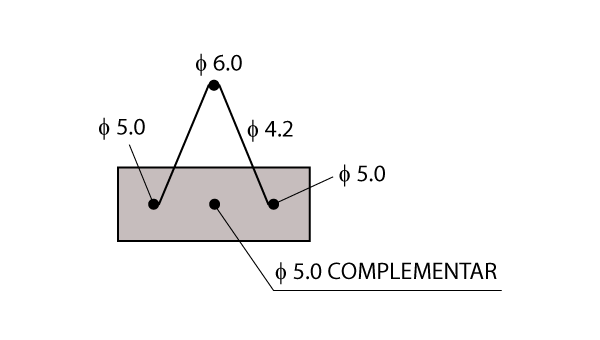
Dimensionamento através de softwares
Para o dimensionamento apresentado analisamos uma nervura isolada. Softwares de cálculo discretizam as lajes nervuradas da mesma maneira, representando-as por um conjunto de barras, conforme apresentado na figura abaixo.
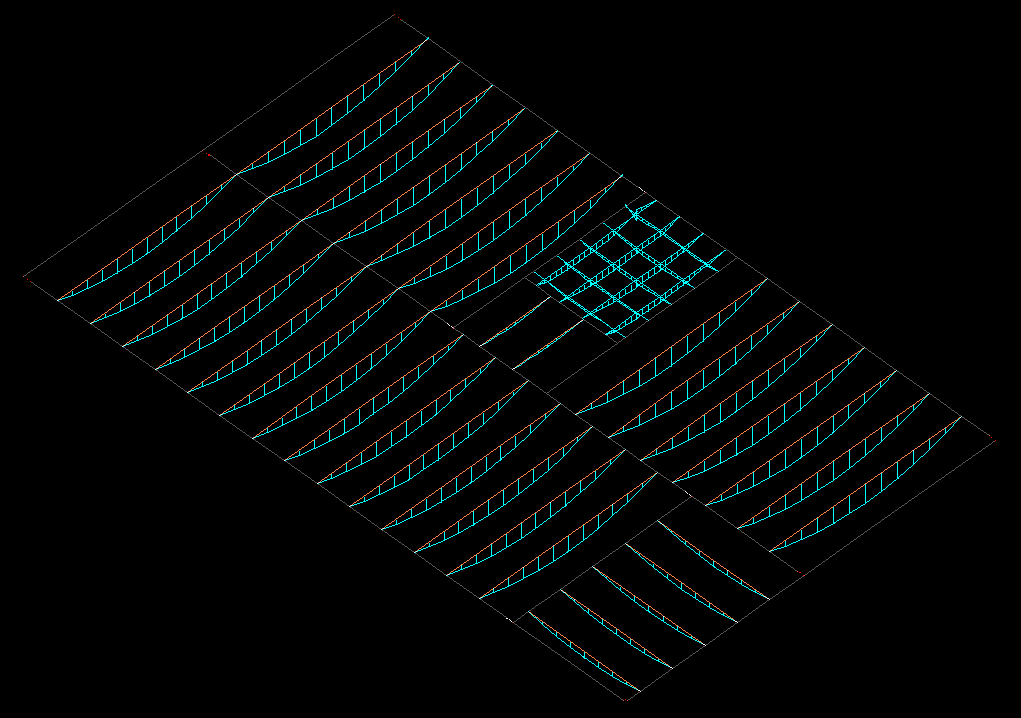
O software TQS possibilita ao engenheiro analisar e dimensionar um conjunto de lajes, confirme apresentado na figura abaixo.
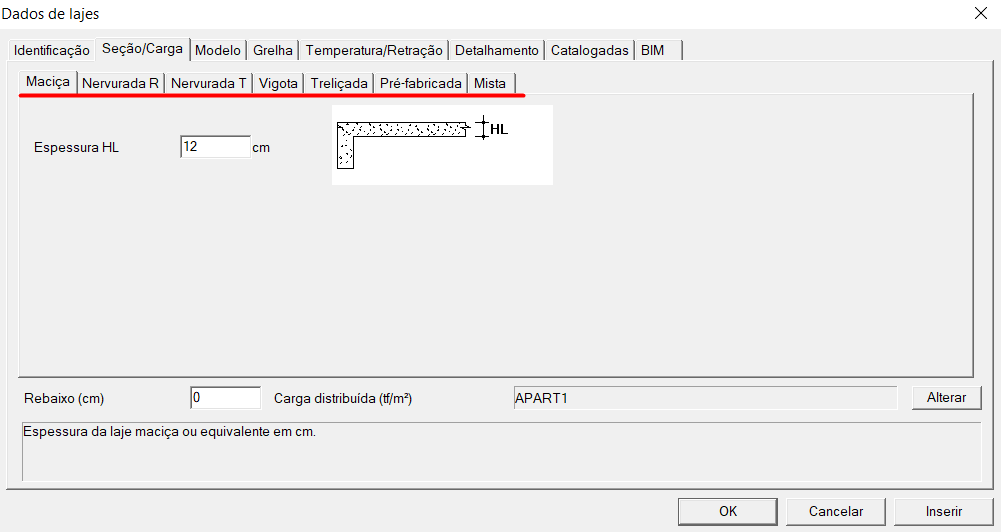
Cabe ao engenheiro configurar completamente os critérios de cálculo para se beneficiar só assim da alta produtividade proporcionada pelo software.
Diante do comentado, convido você a conferir o curso Essencial em Concreto Armado do professor Rangel Lages em que você irá aprender a utilizar o software TQS (na minha opinião, o melhor software do mercado) passando por TODAS as etapas (desde a concepção estrutural até elaboração das pranchas) necessárias para o desenvolvimento de um projeto completo.
Recado final
É importante lembrar que as lajes nervuradas usualmente são limitadas por apresentarem grandes deslocamentos. Logo, após o dimensionamento da armadura de flexão o próximo passo seria verificar os estados limites de serviço.
Até a próxima!
Fonte:
ARAÚJO, J. M. Curso de Concreto Armado. Rio Grande: Editora Dunas, 2014. v. 1
ASSOCIAÇÃO BRASILEIRA DE NORMAS TÉCNICAS. NBR 6118: Projeto de estruturas de concreto – Procedimento. Rio de Janeiro, 2014.
CARVALHO, R. C.; FIGUEIREDO FILHO, J. R. Cálculo e Detalhamento de Estruturas Usuais de Concreto Armado Segundo a NBR 6118:2014. São Carlos: EdUFSCar, 2014.
Gostaria de ter acesso a um curso sobre modelagem de alvenaria estrutural no Revit?
Aproveite enquanto está com um preço especial.

Parabéns pelos materiais. Utilizei vários para estudar, são bem simples e completos!!! Obrigada
Muito obrigado, Patrícia!
Parabéns pelo trabalho, explica muito bem o passo a passo.
Muito obrigado, José!
Fico feliz que tenha gostado,
Abraços!
Bom dia, onde encontro um curso para aprender mais como dimensionar uma laje treliçada, obrigado pela atenção.
Olá, Bruno,
No momento não temos nenhum curso sobre o tema.
Muito obrigado pela sugestão.
Abraços!
Boa noite, ótimo conteúdo. Verifiquem o cálculo da área da seção T, (0,45*0,05)+(0,08*0,12) dá 0,0321m2 e não 0,0123m2
Abraço
Boa iniciativa e boa explicação. Gostaria de saber como é feito o cálculo de nervuras transversais nas lajes unidirecionais
Nesse caso o mais correto seria utilizar modelo de grelha mesmo.
Espero ter ajudado,
abraços!