Nessa primeira publicação sobre lajes maciças nós iremos abordar como obter os esforços em lajes maciças (incluindo considerações sobre o vão teórico e diferentes condições de contorno) e dimensionar a área de aço da armadura principal.
Fica até o final que tem muito conteúdo interessante pela frente!
Ah, já ia me esquecendo! Você também pode acompanhar essa explicação em vídeo:
Obtenção dos esforços
Não era de se esperar diferente que a primeira etapa do dimensionamento de uma laje maciça é fosse a obtenção dos esforços.
Uma vez que, dou preferência à cálculos manuais em minhas publicações, nos ateremos aqui a processos simplificados através de tabelas. Recomendo que você confira na publicação marcada acima sobre as considerações desse método.
Vão teórico
A fim de utilizarmos as tabelas de lajes (como a de Czerny), primeiramente iremos rever o conceito de vão teórico.
É comum utilizarmos como vão teórico simplesmente a distância entre centro dos apoios (no caso de lajes, usualmente temos as vigas como apoio). A norma ABNT/NBR: 6118 (2014) afirma que não é necessário utilizar valores de vãos teóricos superiores à dimensão entre faces dos apoios acrescidos à 60% da espessura da laje.
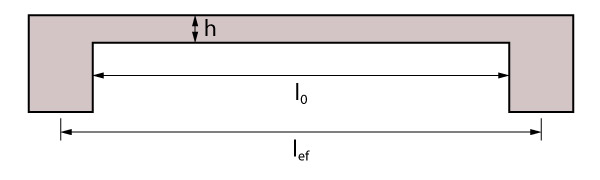
Visto que, normalmente não temos altos valores na largura da viga, não teremos muita diferença em considerar o vão teórico até o eixo dos apoios. Como recomendação pessoal, diria para pensar inicialmente na situação em que o vão teórico vai até o centro do apoio, mudando apenas em situações de apoios maiores.
Condições de contorno
Além das dimensões da laje maciça, para obtermos os esforços em lajes maciças e então calcularmos a armadura necessária, é necessário definirmos quais as condições de contorno da mesma, ou seja, quais as vinculações que suas bordas estão submetidas.
Em resumo, podemos considerar três vinculações possíveis:
- borda engastada;
- bordas simplesmente apoiada;
- borda livre.

Em primeiro lugar, em bordas engastadas, não teremos translações e nem rotação nessa extremidade.
Em seguida, no caso de bordas simplesmente apoiadas, a laje não apresentará translações naquela extremidade mas estará livre à rotação.
Por fim, as bordas livres não apresentam nenhum tipo de restrição externa, ou seja, a laje não terá nenhuma restrição de deslocamentos naquela extremidade.
Diferentes condições em uma mesma borda
Dependendo da sua planta de forma, pode ocorrer mais de uma das condições de contorno apresentadas acima em uma mesma borda. A forma que iremos prosseguir irá variar de acordo com a proporção entre as duas condições de contorno.
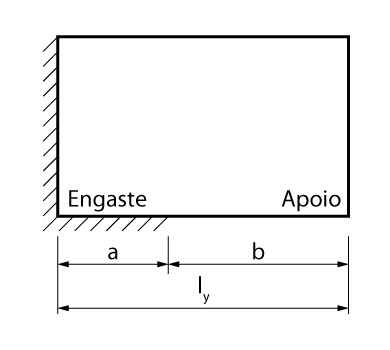
- primeiramente, vamos considerar a borda inferior como simplesmente apoiada caso o valor de \mathrm{a} seja \mathrm{a \leq \dfrac{l_y}{3}};
- de maneira análoga, caso \mathrm{b \leq \dfrac{l_y}{3}}, consideraríamos a borda como inteiramente engastada;
- enfim, caso nenhuma das condições acima sejam atendidas, é recomendado realizar o cálculo para as duas situações e atender os maiores valores de dimensionamentos obtidos.
Grandes diferenças de momentos negativos
Dependendo dos vãos e dos carregamentos atuantes em duas lajes adjacentes, é possível que os resultados obtidos não sejam satisfatórios, divergindo bastante da realidade.
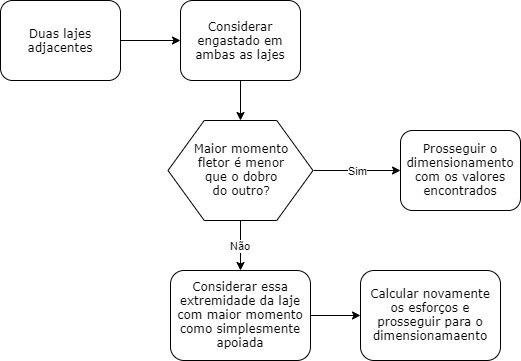
Vou apresentar agora algumas recomendações de consideração ou não de engaste para cálculos manuais.
No caso do maior momento negativo ser superior ao dobro do menor momento negativo, é interessante que os cálculos sejam refeitos considerando que a laje do maior momento esteja simplesmente apoiado na laje do menor momento. A afirmação acima foi colocada de forma mais didática no fluxograma abaixo.
Compatibilização dos momentos fletores
Uma vez que, através de métodos simplificados nós calculamos os esforços de duas lajes adjacentes isoladamente, é possível (e provável), como acabo de comentar, obtermos valores diferentes no momento negativo de intersecção.
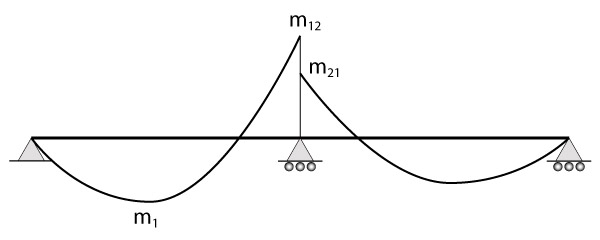
A princípio, iremos corrigir o momento fletor negativo. Assim sendo, vamos considerar o maior valor entre a média dos dois momentos negativos e 80% do maior dos momentos negativos.
\mathrm{m_{12}^* \geq \left\{ \begin{array}{ll} \dfrac{m_{12} + m_{21}}{2} \\ 0,8 \cdot m_{12} \end{array} \right. }
Perceba que a redução do momento \mathrm{m_{12}} é acompanha de um aumento no momento \mathrm{m_1}. Esse aumento equivale a metade da redução ocorrida no momento negativo.
\mathrm{m_1 ^* = m_1 + \dfrac{m_{12} - m_{12}^*}{2}}
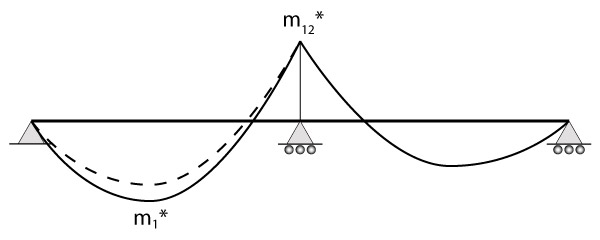
Enquanto isso, para o momento \mathrm{m_2}, a favor da segurança, não alterarmos.
Carregamentos em lajes maciças
Diferente do que abordamos em lajes nervuradas e escadas de concreto armado, para lajes maciças os carregamentos tem uma obtenção bem mais direta. As lajes maciças estão submetidas comumente aos seguintes carregamentos:
- peso próprio;
- revestimento;
- sobrecarga de utilização
A seguir, irei apresentar como obter os valores usuais para o dimensionamento de lajes maciças.
Peso próprio
A fim de calcularmos o peso próprio, basta multiplicar a espessura da laje pelo peso específico do concreto armado, que de acordo com a ABNT/NBR: 6120 (2019) vale \mathrm{25 \; kN/m^2}.
\mathrm{g_1 = h \cdot \gamma_c}
Revestimento
O carregamento decorrente do revestimento irá variar de acordo com o detalhamento da arquitetura. Os pesos específicos de diversos materiais podem ser obtidos diretamente da ABNT/NBR: 6120 (2019). Em caso usuais, recomendo utilizar um carregamento \mathrm{g_2 = 1,0 \; kN/m^2}
Sobrecarga de utilização
Semelhantemente ao revestimento também iremos verificar na norma ABNT/NBR: 6120 (2019) os valores de sobrecarga de utilização (também denominada de carga acidental). Conforme o nome indica, o valor irá variar de acordo com a utilização sobre a laje.
Só para exemplificar, a tabela abaixo apresenta os valores para obras residências, de acordo com o cômodo da laje.
| Cômodo | Carregamento (kN/m²) |
|
Dormitórios Sala, copa, cozinha Sanitários Corredores dentro de unidades autônomas |
1,5 |
| Despensa, área de serviço e lavanderia | 2,0 |
Classificação quanto à armação em lajes maciças
As lajes maciças podem ser ainda divididas em duas situações:
- lajes armadas em uma direção;
- lajes armadas em duas direções.
Primeiramente, as lajes são consideradas armadas em uma direção quando uma das direções possui pelos menos o dobro da outra. Assim sendo, o momento na direção maior pode ser desconsiderado. A obtenção dos esforços para essa laje é realizado com um modelo simplificado de barras apenas no sentido da menor direção, conforme realizado em lajes nervuradas.
Em segundo lugar, em que a razão entre as dimensões das duas direções é inferior a 2, a laje maciça é dita como armadura em duas direções (ou em cruz). Nessa situação, a obtenção dos esforços é feito a partir de modelos numéricos ou tabelas simplificadas (o que utilizaremos).
Entrando nas tabelas de Czerny
Para essa publicação, prosseguiremos o cálculo de lajes maciças com as tabelas de Czerny, mas você pode escolher outra de sua preferência.
Antes de mais nada, gostaria de destacar os dados de entrada das tabelas:
- Razão entre as dimensões;
- Carregamento atuante por unidade de área;
- Condições de contorno da laje.
A razão entre as dimensões é dada pela seguinte formulação:
\mathrm{\lambda = \dfrac{l_y}{l_x}}
Em que \mathrm{l_y} e \mathrm{l_x} indicam, respectivamente, a maior e a menor dimensão da laje e podem ser considerados como os vãos teóricos já explicados anteriormente.
Uma vez que já conhecemos as condições de contorno da laje e o carregamento distribuído uniformemente, podemos entrar nas tabelas apresentadas abaixo e calcular o esforços.
Enfim, com os valores de \mathrm{m_x}, \mathrm{m_y}, \mathrm{n_x}, \mathrm{n_y}, \mathrm{v_x} e \mathrm{v_y} retirados da tabela é possível calcularmos os momentos fletores positivos e negativos assim como os esforços cortantes.
\mathrm{M_x = \dfrac{p \cdot l_x^2}{m_x}}
\mathrm{M_y = \dfrac{p \cdot l_x^2}{m_y}}
As formulações colocada assim estão presentes no arquivo no formato PDF em que a tabela está contida. No caso do momento fletor, apenas como exemplo, a saída seria em \mathrm{kN \cdot m / m}
Dimensionamento da área de aço de lajes maciças
O dimensionamento da área de aço de uma laje maciça é o mesmo realizado para elementos submetidos à flexão simples e pura, conforme já abordado para vigas de concreto. Como já foi tratado na publicação acima, não vou avançar nas explicações nessa publicação.
A única consideração interessante que gostaria de acrescentar é quanto ao valor de \mathrm{b_w}. É interessante que o mesmo seja considerado igual a 100 cm, uma vez que os esforços foram para cada metro de largura. Dessa forma, obteremos uma área de aço também para cada metro de largura.
Caso você tenha interesse de obter a nossa calculadora de flexão simples, que pode ser utilizada para calcular lajes maciças, basta preencher o formulário abaixo.
[formulario-calculadora-flexao]Ademais, lembre-se que existem outros pontos a serem verificados em uma laje maciça, como por exemplo: regras de detalhamento e armaduras mínimas, deslocamentos excessivos e verificações de cisalhamento. Dessa maneira, não pare seu estudo por aqui, procure outras publicações ou vídeos para sempre se aperfeiçoar mais nesse conteúdo.
Recado final
Parabéns por ter chegado até aqui! Nesse momento você aprendeu a base para o dimensionamento de lajes maciças. Se você gostou desse texto ou se ainda possui alguma dúvida sobre o cálculo de lajes maciças, deixe uma mensagem nos comentários abaixo!
Caso tenho interesse de seguir nessa área de cálculo estrutural eu recomendo que você confira o curso Essencial em Concreto Armado do professor Rangel Lage em que você irá aprender a utilizar o software TQS (na minha opinião, o melhor software do mercado) passando por TODAS as etapas (desde a concepção estrutural até elaboração das pranchas) necessárias para o desenvolvimento de um projeto completo.
Fonte:
ARAÚJO, J. M. Curso de Concreto Armado. Rio Grande: Editora Dunas, 2014. v. 2
PINHEIRO, L. M, MUZARDO, C. D. SANTOS S. P. Lajes maciças. 2013 Notas de Aula.
ASSOCIAÇÃO BRASILEIRA DE NORMAS TÉCNICAS. NBR 6118: Projeto de estruturas de concreto – Procedimento. Rio de Janeiro, 2014.
Gostaria de ter acesso a um curso sobre modelagem de alvenaria estrutural no Revit?
Aproveite enquanto está com um preço especial.
