A obtenção analítica dos esforços em lajes maciças armadas em duas direções é um processo bem mais complexo do que a obtenção dos esforços em lajes nervuradas ou lajes maciças armadas em uma direção. Em situações mais comuns, tais esforços podem ser obtidos de maneira simplificada por meio de tabelas.
Neste post você aprenderá a utilizar as tabelas citadas acima e verá uma comparação dos resultados obtidos através das tabelas e de processos mais refinados.
Utilização de tabelas
Nós utilizaremos as tabelas de Czerny e Libânio (adaptado de Bares) para o estudo. Inicialmente é necessário conhecermos as condições de contorno a que a laje está submetida. A figura abaixo representa as condições de contorno abordadas pelas tabelas, que são: borda engastada, borda apoiada e borda livre.

Essas tabelas foram elaboradas com base na consideração de apoios indeslocáveis, ou seja, para o caso de arestas engastadas ou apoiadas o deslocamento vertical é assumido como nulo, situação que muitas vezes não representa a condição real.
Nas duas tabelas, além das condições de contorno, utiliza-se a razão entre a dimensão maior e a dimensão menor da laje:
\mathrm{\lambda = \dfrac{l_y}{l_x}}
Apesar da semelhança, cada tabela possui formulações distintas:
| Czerny | Libânio |
| \mathrm{\dfrac{p \cdot {l_x}^2}{m}} | \mathrm{\mu \cdot \dfrac{p \cdot {l_x}^2}{100}} |
Onde p simboliza o carregamento uniformemente distribuído em kN/m², \mathrm{l_x} a menor dimensão da laje e m e \mathrm{\mu} representam os valores retirados, respectivamente, das tabelas de Czerny e Libânio.
Exemplo aplicado
Apenas como exemplo vamos analisar uma laje de 4,8 m por 4,0 m utilizando a tabela de Libânio. A laje é simplesmente apoiada nas quatro arestas e está submetida a um carregamento de 3 kN/m².
\mathrm{\lambda = \dfrac{l_y}{l_x}=\dfrac{4,8 \; m}{4,0 \; m}=1,2 }
\mathrm{p \cdot {l_x}^2 = 3 \cdot 4^2 = 48}
A figura abaixo apresenta a utilização da tabela. Para uma laje simplesmente apoiada com \mathrm{\lambda = 1,2}, obtemos os valores 5,75 para direção x e 4,22 para direção y.
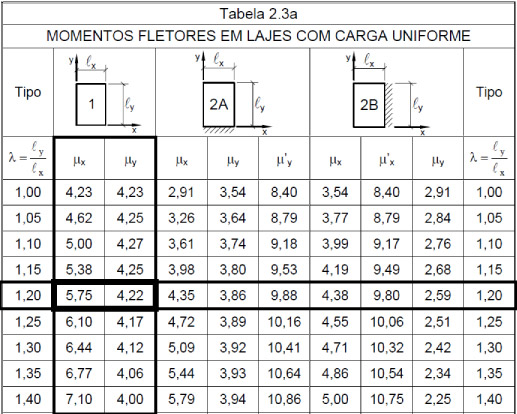
A partir do valores retirados da tabela é possível calcular os momentos fletores nas duas direções:
\mathrm{M_x = 5,75 \cdot \dfrac{48}{100}=2,76 \; kN \cdot m / m}
\mathrm{M_y = 4,22 \cdot \dfrac{48}{100}=2,03 \; kN \cdot m / m}
Comparação com o modelo de grelha equivalente
A fim de estudar a utilização dessas tabelas, iremos utilizar um programa de modelagem de grelha com intuito de comparar com momentos fletores fornecidos pelas tabelas. O objeto de estudo será uma laje quadrada de 4,0 m, 10 cm de espessura e solicitada por um carregamento de 2 kN/m².
A mesma está apoiadas em quatro vigas, que irão variar de inércia em cada caso analisado, sobre pilares de 20 x 20 em cada vértice da laje. Uma vez que as tabelas não levam em conta a inércia das vigas de apoio (considerado sempre apoios indeslocáveis), não será necessário refazer os esforços obtidos a partir das tabelas para cada caso.
A partir das tabelas de Czerny e de Libânio foram obtidos, respectivamente os momentos de 1,41 kN.m e 1,35 kN.m em ambas as direções.
Caso 1: Apoios indeslocáveis
Nesse caso, vamos assumir apoios indeslocáveis, conforme a consideração adotada para a confecção das tabelas. Para isso, utilizaremos vigas com a inércia alterada manualmente para valores bastante elevados, afim de garantir a indeslocabilidade das mesmas.
A figura abaixo ilustra o deslocamento apresentado pela a laje do caso 1, em que é possível perceber que não ocorre deslocamentos em nenhum ponto no contorno da laje.
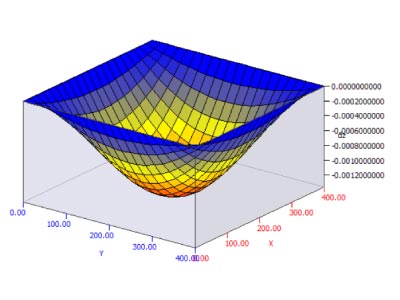
Nesse caso, a análise de grelha equivalente resultou em um momento máximo, nas duas direções, de 1,37 kN.m/m.
Caso 2: Vigas de 20 x 40 cm
No segundo caso, utilizaremos vigas deslocáveis com dimensões usuais para esse vão. Pré-dimensionando as mesmas com 1/10 do vão, ou seja, 40 cm.
Na imagem abaixo, diferentemente da anterior, já é possível perceber deslocamentos ao longo das arestas da laje, apresentando assim, indeslocabilidade apenas na posição dos pilares.
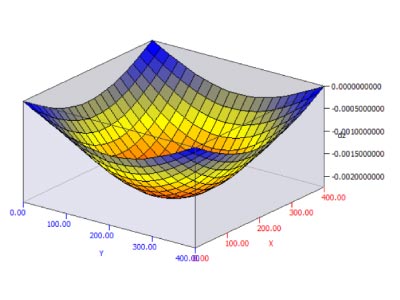
Para esse caso foi obtido um momento fletor máximo de 1,51 kN.m/m nas duas direções.
Caso 3: Direções com apoios diferentes
No terceiro e último caso estudado, manteremos duas vigas paralelas com 20 x 40 cm e na outra direção (aqui denominada de y) utilizaremos duas vigas paralelas de 20 x 80 cm.
É fácil perceber na imagem abaixo a posição das vigas de 20 x 80 cm e das vigas de 20 x 40 cm.
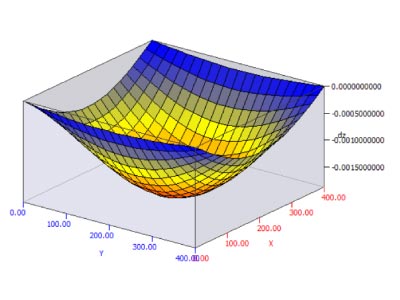
Ao observar os esforços na grelha, percebe-se que não existe uma igualdade de momentos fletores nas duas direções. O que ocorre de fato é que a laje trabalha mais na direção do apoio rígido, ou seja, os esforços são maiores na direção apoiada pelas vigas de 20 x 80 cm.
Os momentos fletores nas direções x e y são, respectivamente, 1,63 kN.m/m e 1,26 kN.m/m.
Resumo
A tabela abaixo apresenta um resumo da comparação dos momentos fletores obtidos nas duas tabelas e no modelo de grelha equivalente para os três casos estudados:
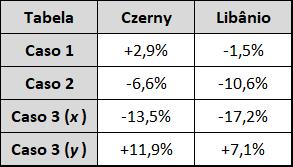
Para o caso 1, que é similar a situação prevista na elaboração das tabelas, os resultados apresentados em Czerny e em Libânio foram bem próximos do modelo de grelha, conforme era esperado.
Para os casos 2 e 3, foi obtida uma diferença máxima de 17,2% em relação ao modelo de grelha. Apesar da diferença elevada, alguns pontos devem ser observados:
- Uma parcela do coeficiente que majora as ações já é considerado para prever erros no método de cálculo empregado;
- Ao dimensionar uma laje por métodos aproximados, esse momento calculado é utilizado para dimensionar a armadura que será distribuída em toda a laje. De fato, ao analisarmos regiões próximas ao apoio, obtemos esforços bem inferiores aos obtidos nas regiões centrais;
- Em especial para o caso 3, em que obteve-se a maior diferença, deve-se observar que, para direção x tivemos resultados na tabela inferiores aos obtidos no modelo de grelha, mas para direção y, obtivemos resultados superiores. Obtendo de fato uma reserva resistente.
Devido a alta hiperestaticidade das lajes, ao uma seção atingir limites de capacidade resistente, ocorrerá uma redistribuição dos esforços para seções vizinhas.
É importante ter ciência que a comparação foi realizada apenas para uma única laje quadrada, em que o restante do pavimento não estava presente no modelo. Por isso, o domínio de um software com uma boa capacidade de análise estrutural é muito importante na atualidade.
Se ainda ficou com alguma dúvida, deixe nos comentários abaixo!
Gostaria de ter acesso a um curso sobre modelagem de alvenaria estrutural no Revit?
Aproveite enquanto está com um preço especial.
