Uma peça de concreto armado submetida a um momento fletor crescente apresenta três níveis de deformação até a sua ruptura, que são denominados de estádios de deformação.
Nesse post você aprenderá esse conteúdo que é base para muitas questões na engenharia estrutural.
Definição dos estádios
Caso prefira, você pode acompanhar esse primeiro tópico de definição pelo vídeo abaixo:
A seguir, você aprenderá os três estádios de deformação assim como as suas respectivas características.
Estádio I
No primeiro estádio a seção está submetida a um momento fletor \mathrm{M_t} de pequena intensidade, de modo que a tensão de tração no concreto é inferior a sua resistência característica. Dessa forma, a peça ainda não apresenta fissuras visíveis.
Como a resistência a tração não foi atingida, a contribuição do concreto para resistir esse esforço ainda é considerada.
Pode-se considerar que o momento de fissuração, previsto na ABNT/NBR: 6118 (2014), é o limite do estádio I:
\mathrm{M_r = \dfrac{\alpha \cdot f_{ct} \ I_c}{y_t}}
Em uma peça submetida à flexão, parte da seção estará solicitada a tração e a posição oposta à compressão. Diante desse fato, uma vez que a viga não está submetida à tração uniforme, é utilizado o coeficiente \mathrm{\alpha} para correlacionar a resistência a tração na flexão com a tração direta. O mesmo vale 1,2 para seções T ou duplo T, 1,3 para seções I ou T invertido e 1,5 para seções retangulares.
\mathrm{f_{ct}} é resistência à tração direta do concreto e, conforme presente pela ABNT/NBR: 6118 (2014), iremos utilizar porções estatísticas diferentes para cada estado limite verificado.Apenas como exemplo do apresentado acima, para o estado limite de formação de fissura deve ser utilizado o \mathrm{f_{ctk,inf}} enquanto para o estado limite de deformação excessiva deve-se utilizar o \mathrm{f_{ct,m}}.
\mathrm{I_c} é o momento de inércia da seção bruta de concreto. Também pode ser tomado como o momento de inércia no estádio I com a armação incorporada. Assim sendo, é possível aumentar a inércia da peça ao considerar a contribuição da armadura.Por fim, o \mathrm{y_t} é a distância do centro de gravidade à fibra mais tracionada.
Estádio II
No estádio II a resistência a tração do concreto foi atingida, de modo que a peça apresenta fissuras visíveis e a contribuição da parte tracionada do concreto passa a ser desprezada. Nesse momento a distribuição de tensões de compressão no concreto ainda é linear.
Estádio III
No estádio III a peça já está próxima da ruptura e a distribuição de tensões no concreto não é mais linear.
Correlação entre estádios de deformação e estado limites
Existe uma relação direta entre os estádios de deformação e os estados limites: normalmente as verificações em serviço são realizadas com seções nos estádios I e II, atuando as ações reais, enquanto as verificações últimas de situações extremas são correspondem a seções no estádio III.
A figura abaixo apresenta um resumo contendo a distribuição de tensões em seções que caracterizam os três estádios comentados anteriormente.
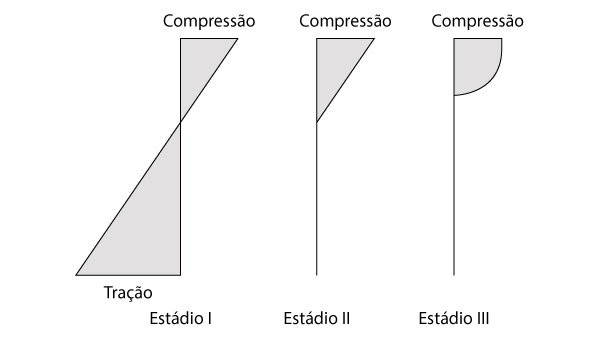
Propriedades da seção no estádio I
Agora que você já aprendeu os conceitos por trás dos estádios do concreto, vamos avançar para obtenção da rigidez em cada um desses estádios.
Para a seção atuando no estádio I, a inércia poderia ser calculada considerando apenas o concreto, mas mesmo assim consideraremos o ganho de inercia fornecido pela armadura.
A seguir são apresentadas formulações de Carvalho e Figueiredo para a área da seção, centro de gravidade e inércia considerando a armação em uma seção no formato T.
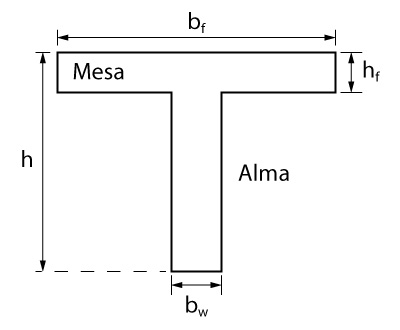
Primeiramente vamos calcular a área da seção levando em consideração a área de aço:
\mathrm{A_h=(b_f-b_w) \cdot h_f + b_w \cdot h + \cdots}
\mathrm{+ A_s \cdot (\alpha - 1)}
Para essa formulação a armadura foi levada em consideração ao converter a área de aço em uma área de concreto equivalente a partir de um fator \mathrm{\alpha = \dfrac{E_s}{E_c}}.
O centro de gravidade da seção homogeneizada pode ser obtida a partir da equação abaixo:
\mathrm{y_{h}= \dfrac{(b_f-b_w) \cdot \dfrac{h_f^2}{2} + b_w \cdot \dfrac{h^2}{2}}{A_h} + \cdots}
\mathrm{+ \dfrac{A_s \cdot (\alpha - 1) \cdot d}{A_h}}
Por fim, podemos calcular o momento de inércia da seção homogeneizada:
\mathrm{I_h = \dfrac{(b_f - b_w) \cdot h_f^3}{12} + \dfrac{b_w \cdot h^3}{12} + \cdots}
\mathrm{+ (b_f - b_w) \cdot h_f \cdot (y_h - \dfrac{h_f}{2})^2 + \cdots}
\mathrm{+ b_w \cdot h \cdot (y_h - \dfrac{h}{2})^2 + \cdots}
\mathrm{+ A_s \cdot (\alpha - 1) \cdot (y_h - d)^2}
Propriedades da seção no estádio II
Assim como realizado para o estádio I, essas são as formulações apresentadas por Carvalho e Figueiredo para a inércia no estádio II de uma peça com seção em formato de T.
É válido lembrar que para o estádio II a consideração da armação não é opcional, uma vez que é assumido que o concreto já não resiste mais a tração nesse momento.
Vamos inicialmente obter a posição da linha neutra para essa situação:
\mathrm{x_{II} = \dfrac{-b \pm \sqrt{b^2 - 4 \cdot a \cdot c}}{2 \cdot a}}
Onde:
\mathrm{a= \dfrac{b_w}{2}}
\mathrm{b = h_f \cdot (b_f - b_w) + \cdots}
\mathrm{+ (\alpha_e -1) \cdot A_s' + \alpha_e \cdot A_s}
\mathrm { c = d' \cdot (\alpha_e -1) \cdot A_s' + \cdots }
\mathrm { - d \cdot \alpha_e \cdot A_s - \dfrac{h_f^2}{2} \cdot (b_f - b_w) }
A inércia no estádio II dependerá se a linha neutra da peça caiu dentro ou fora da mesa:
Caso a linha neutra tenha caído dentro da mesa \mathrm{x_{II} \leq h_f}:
\mathrm{I_{II} = \dfrac{b_f \cdot x_{II}^3}{3} + \alpha_e \cdot A_s \cdot (x_{II}-d)^2 + \cdots}
\mathrm { + (\alpha_e -1) \cdot A_s' \cdot (x_{II} - d')^2 }
Caso a linha neutra tenha caído fora da mesa \mathrm{x_{II} > h_f}:
\mathrm { I_{II} = \dfrac{ (b_f - b_w) \cdot h_f^3 }{12} + \dfrac{b_w \cdot x_{II}^3}{3} + \cdots }
\mathrm { + (b_f - b_w) \cdot h_f \cdot (x_{II} - \dfrac{h_f}{2})^2 + \cdots}
\mathrm {+ \alpha_e \cdot A_s \cdot (x_{II} - d')^2 }
Exemplo aplicado
Vamos supor uma viga de concreto C20 com de 15 cm de largura e 40 cm de altura, vencendo um vão de 5,0 m e submetida a uma carregamento de 8 kN/m. O objetivo desse exemplo é analisar em que estádio se encontra a seção mais solicitada e qual sua inércia.
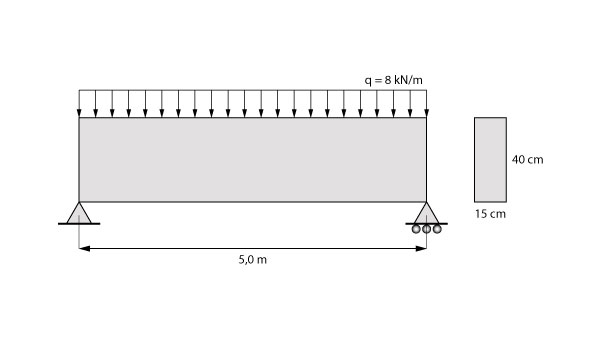
Descobrindo em que estádio a peça se encontra
Inicialmente é necessário calcular o máximo esforço a que essa viga está solicitada:
\mathrm{M_{máx} = \dfrac{q \cdot L^2}{8} = \dfrac{8 \cdot 5^2}{8} = 25 \; kN \cdot m}
Agora temos que verificar se essa seção atingiu o momento de fissuração do concreto:
\mathrm { M_r = \dfrac {\alpha \cdot f_{ct,m} \cdot I} {y_t} }
Assumiremos que essa análise tem por fim verificação do estado limite de deformação excessiva. Sendo assim, o valor da resistência à tração direta \mathrm{f_{ct}} foi tomado como o seu valor valor médio \mathrm{f_{ct,m}}.
\mathrm { f_{ct,m} = 0,3 \cdot {f_{ck}}^{\frac{2}{3}} = 0,3 \cdot 20^{\frac{2}{3}} }
\mathrm {f_{ct,m} = 2,21 \; MPa = 0,221 \; kN/cm^2}
A inércia será calculada apenas pela seção bruta de concreto, ou seja, para o estádio I desconsideraremos a contribuição da armadura.
\mathrm { I = \dfrac{b \cdot h^3}{12} = \dfrac{15 \cdot 40^3}{12} = 80000 \; cm^4 }
Por fim, o coeficiente \mathrm{\alpha} é assumido como 1,5, uma vez que se trata de uma seção retangular.
\mathrm { M_r = \dfrac{\alpha \cdot f_{ct,m} \cdot I}{y_t} = \dfrac{1,5 \cdot 0,221 \cdot 80000}{20} }
\mathrm { M_r = 1326 \; kN \cdot cm}
Visto que o momento solicitante \mathrm{(2500 kN \cdot cm)} é superior ao momento de fissuração \mathrm{(1326 kN \cdot cm)} prosseguiremos com o cálculo da inércia para o estádio II.
De acordo com a relação entre o momento atuante e o momento de fissuração é possível obtermos inercias intermediárias entre os estádios I e II (através da formulação de Branson), mas isso não é conteúdo para essa publicação.
Cálculo do momento de inércia para o estádio II
Calcularemos inicialmente a posição da linha neutra para a seção no estádio II. É válido ressaltar que mesmo as formulações apresentadas acima serem para seções em formato T, as mesmas são facilmente adaptáveis para seções retangulares.
\mathrm { a = \dfrac{b_w}{2} = \dfrac{15}{2} = 7,5 }
\mathrm { b = \alpha \cdot A_s = 9,865 \cdot 1,6 = 15,784 }
\mathrm { c = -d \cdot \alpha \cdot A_s = - 37 \cdot 9,865 \cdot 1,6 = -584,008}
\mathrm { x_{II} = \dfrac{-b \pm \sqrt{b^2 - 4 \cdot a \cdot c}}{2 \cdot a} }
\mathrm { x_{II} = \dfrac{-15,784 \pm \sqrt{15,784^2 - 4 \cdot 7,5 \cdot (-584,008)}}{2 \cdot 7,5} }
\mathrm { x_{II} = \left\{ \begin{array}{ll} 7,835 \; cm \\ -9,939 \; cm \end{array} \right. }
Se tratando de um caso de flexão simples (sem a presença de esforço normal), não faria sentido a linha neutra fora da seção transversal. Logo, a possibilidade da raiz negativa é excluída.
Utilizando então a raiz positiva como o valor para a linha neutra, calcula-se por fim o valor do momento de inércia:
\mathrm { I_{II} = \dfrac{15 \cdot 7,835^3}{3} + 9,865 \cdot 1,6 \cdot (7,835 - 37)^2 }
\mathrm { I_{II} = 15830,67 \; cm^4 }
Observe que o valor do momento de inércia no estádio II é 19,8% do valor encontrado anteriormente considerando a seção bruta de concreto. Os conceitos aprendidos nesse exemplo serão muito úteis futuramente quando verificarmos situações de serviço.
Se você gostou desse texto ou se ainda possui alguma dúvida, deixe uma mensagem nos comentários abaixo!
Gostaria de ter acesso a um curso sobre modelagem de alvenaria estrutural no Revit?
Aproveite enquanto está com um preço especial.

Parabéns , mais um belo trabalho. Grato por vocês compartilharem todo esse conhecimento de maneira simples e eficaz.
Muito obrigado pelo apoio, Matheus!
Parabéns pela página esta me ajudando muito nesse final de curso, só me arrependo de não tê-lá encontrado antes.
Muito obrigado pelo comentário e pela correção que mandou por mensagem, Luiz!
Grande Abraço!
Muito bem explicado, parabéns.
Obrigado, Humberto!
A fórmula do momento de inércia no estádio 2 quando x2 > hf está errada!
Segundo o livro cálculo e detalhamento de estruturas usuais de concreto (Carvalho, Filho) quando x2>hf:
I2 = (bf-bw)*hf^3/12+bw*x2^3/3+(bf-bw)*(x2-hf/2)^2+alfa,e*As*(x2-d)^2+(alfa,e-1)*As’*(x2-d’)^2
Espero ter ajudado com o trabalho de vocês
Olá, Gustavo,
Obrigado pela contribuição.
Mas a fórmula do livro não está correta. Basta verificar as unidades.
Abraço!