No nosso post anterior sobre Diagrama de Brückner, explicamos o que é esse diagrama, qual sua importância e também como ele é feito. Se não leu ainda, recomendamos que dê uma olhada.
Agora, vamos solidificar o que foi aprendido sobre Brückner até o momento. Para tanto, propomos um exemplo prático bem simples e, ao final, faremos uma breve interpretação dos resultados.
Confira abaixo!
Exemplo prático
Dado um trecho de uma estrada e suas seções transversais, construa um diagrama de Brückner sabendo que o estaqueamento da estrada é feito a cada 20 m e que o fator de homogeneização é de 1,1.

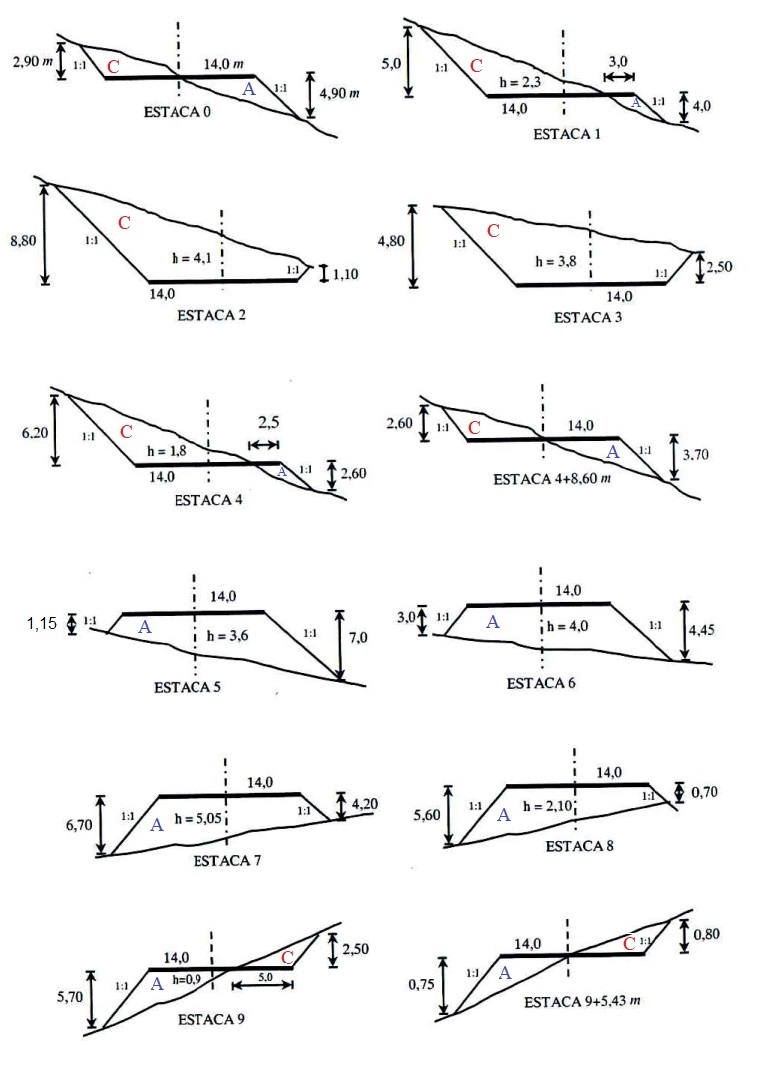
RESOLUÇÃO:
Se preferir, temos toda a resolução dessa questão no vídeo abaixo, é só clicar e conferir!
Mas, se não, é só continuar lendo.
O diagrama de Brückner é feito a partir do quadro de volumes de terraplenagem. Para isso devemos preenchê-lo conforme o passo a passo apresentado a seguir.
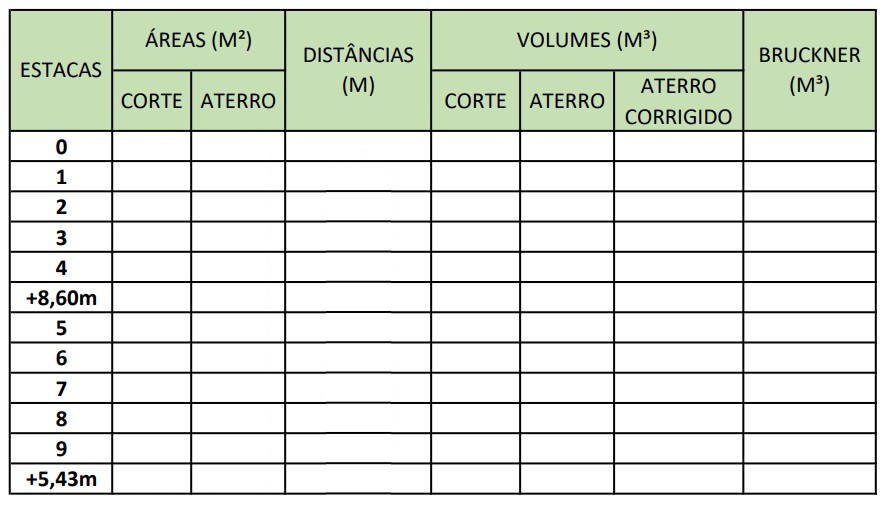
Passo 01: Calcular as áreas de corte e aterro
O cálculo aproximado das áreas de corte e aterro é feito por meio de cálculos geométricos com base nos desenhos das seções transversais fornecidos, conforme abaixo:
Seção 0:
\mathrm{A_{C,0}=\dfrac{(14/2).2,9}{2}=10,15\:m^2}
\mathrm{A_{A,0}=\dfrac{(14/2).4,9}{2}=17,15\:m^2}
Seção 1:
\mathrm{A_{C,1}=\dfrac{(14-3).5}{2}=27,50\:m^2}
\mathrm{A_{A,1}=\dfrac{3.4}{2}=6,00\:m^2}
Seção 2:
\mathrm{A_{C,2}=\dfrac{[14+(14+1,1.2)]1,1}{2}+...}
\mathrm{...+\dfrac{(14+1,1.2).(8,8-1,1)}{2}=78,98\:m^2}
\mathrm{A_{A,2}=0}
Seção 3:
\mathrm{A_{C,3}=\dfrac{[14+(14+2,5.2)]2,5}{2}+...}
\mathrm{...+\dfrac{(14+2,5.2).(4,8-2,5)}{2}=63,10\:m^2}
\mathrm{A_{A,3}=0}
Seção 4:
\mathrm{A_{C,4}=\dfrac{(14-2,5).6,2}{2}=35,65\:m^2}
\mathrm{A_{A,4}=\dfrac{2,5.2,6}{2}=3,25\:m^2}
Seção 4+8,60 m:
\mathrm{A_{C,4+}=\dfrac{2,6.(14/2)}{2}=9,10\:m^2}
\mathrm{A_{A,4+}=\dfrac{3,7.(14/2)}{2}=12,95\:m^2}
Seção 5:
\mathrm{A_{C,5}=0}
\mathrm{A_{A,5}=\dfrac{[14+(14+1,15.2)]1,5}{2}+...}
\mathrm{...+\dfrac{(14+1,15.2).(7-1,15)}{2}=65,10\:m^2}
Seção 6:
\mathrm{A_{C,6}=0}
\mathrm{A_{A,6}=\dfrac{[14+(14+3.2)]3}{2}+...}
\mathrm{...\dfrac{(14+3.2).(4,45-3)}{2}=65,50\:m^2}
Seção 7:
\mathrm{A_{C,7}=0}
\mathrm{A_{A,7}=\dfrac{[14+(14+4,42.2)]4,42}{2}+...}
\mathrm{...+\dfrac{(14+4,42.2).(6,7-4,42)}{2}=104,44\:m^2}
Seção 8:
\mathrm{A_{C,8}=0}
\mathrm{A_{A,8}=\dfrac{[14+(14+0,7.2)]0,7}{2}+...}
\mathrm{...+\dfrac{(14+0,7.2).(5,60-0,7)}{2}=48,02\:m^2}
Seção 9:
\mathrm{A_{C,9}=\dfrac{5.2,5}{2}=6,25\:m^2}
\mathrm{A_{A,9}=\dfrac{(14-5).5,7}{2}=25,65\:m^2}
Seção 9+5,43 m:
\mathrm{A_{C,9+}=\dfrac{0,8.(14/2)}{2}=2,80\:m^2}
\mathrm{A_{A,9+}=\dfrac{0,75.(14/2)}{2}=2,63\:m^2}
Passo 02: Calcular os volumes de corte e aterro
O cálculo do volume aproximado compreendido entre duas estacas também é feito por meio da geometria, de acordo com o esquema abaixo:
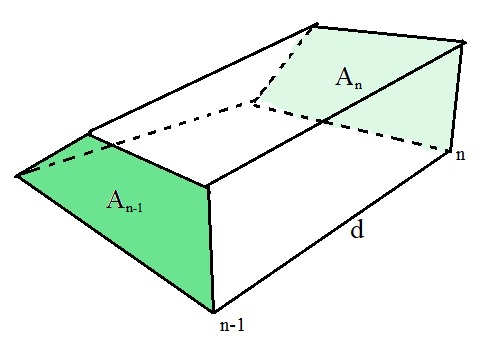
\mathrm{V=\dfrac{(A_{n-1}+A_{n}).d}{2}}
Onde:
- An-1 é a área de corte ou de aterro de um seção n-1 (m²);
- An é a área de corte ou de aterro de um seção n (m²);
- d é a distância entre essas duas seções (m).
Volume entre 0 e 1:
\mathrm{V_{C,01}=\dfrac{(10,15+27,50).20}{2}=376,50\:m^3}
\mathrm{V_{A,01}=\dfrac{(17,15+6).20}{2}=231,50\:m^3}
Volume entre 1 e 2:
\mathrm{V_{C,12}=\dfrac{(27,50+78,98).20}{2}=1064,80\:m^3}
\mathrm{V_{A,12}=\dfrac{(6+0).20}{2}=60,00\:m^3}
Volume entre 2 e 3:
\mathrm{V_{C,23}=\dfrac{(78,98+63,10).20}{2}=1420,80\:m^3}
\mathrm{V_{A,23}=\dfrac{(0+0).20}{2}=0}
Volume entre 3 e 4:
\mathrm{V_{C,34}=\dfrac{(63,10+35,65).20}{2}=987,50\:m^3}
\mathrm{V_{A,34}=\dfrac{(0+3,25).20}{2}=32,50\:m^3}
Volume entre 4 e 4+8,60 m:
\mathrm{V_{C,44+}=\dfrac{(35,65+9,10).8,60}{2}=192,43\:m^3}
\mathrm{V_{A,44+}=\dfrac{(3,25+12,95).8,60}{2}=69,66\:m^3}
Volume entre 4+8,60 m e 5:
\mathrm{V_{C,4+5}=\dfrac{(9,10+0).(20-8,60)}{2}=51,87\:m^3}
\mathrm{V_{A,4+5}=\dfrac{(12,95+65,1).(20-8,60)}{2}=444,89\:m^3}
Volume entre 5 e 6:
\mathrm{V_{C,56}=\dfrac{(0+0).20}{2}=0}
\mathrm{V_{A,56}=\dfrac{(65,1+65,5).20}{2}=1306,00\:m^3}
Volume entre 6 e 7:
\mathrm{V_{C,67}=\dfrac{(0+0).20}{2}=0}
\mathrm{V_{A,67}=\dfrac{(65,5+104,44).20}{2}=1699,40\:m^3}
Volume entre 7 e 8:
\mathrm{V_{C,78}=\dfrac{(0+0).20}{2}=0}
\mathrm{V_{A,78}=\dfrac{(104,44+48,02).20}{2}=1524,60\:m^3}
Volume entre 8 e 9:
\mathrm{V_{C,89}=\dfrac{(0+6,25).20}{2}=62,50\:m^3}
\mathrm{V_{A,89}=\dfrac{(48,02+25,65).20}{2}=736,70\:m^3}
Volume entre 9 e 9+5,43 m:
\mathrm{V_{C,99+}=\dfrac{(6,25+2,8).5,43}{2}=24,57\:m^3}
\mathrm{V_{A,99+}=\dfrac{(25,65+2,63).5,43}{2}=76,77\:m^3}
Passo 03: Corrigir o volume de aterro
Para corrigir o volume de aterro realmente necessário, devemos considerar o grau de compactação do material granular no aterro.
Para isso, observe a imagem abaixo:
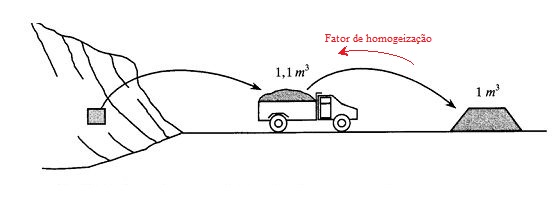
Podemos observar que o material granular retirado de um corte está no seu estado de compactação natural.
Quando esse material é escavado e transportado até um aterro, ele adquire um novo grau de compactação, em outras palavras, se torna menos compactado que no estado natural.
Por fim, quando esse material é depositado em um aterro, será necessário compactá-lo até um grau desejado.
Dessa forma, o volume de corte necessário para realizar um aterro deverá ser maior que o necessário, tendo em vista que este volume deverá ser compactado. Portanto, a essa transição de graus de compactação de corte para aterro dá-se o nome de fator de homogeneização.
Sabendo disto, para realizar a correção do real volume necessário para aterro, basta multiplicarmos o volume do aterro calculado até agora pelo fator de homogeneização = 1,1.
Passo 04: Calcular as ordenadas de Brückner
Para o cálculo da última coluna do quadro de volumes, devemos inicialmente arbitrar um valor qualquer de Brückner para a estaca inicial.
Esse valor arbitrado tem o único objetivo de evitar valores de Brückner negativos e em nada influencia no resultado final. Portanto, nesse exemplo adotaremos um valor inicial de 5000 m³.
Feito isso, o valor de Brückner da próxima estaca será a diferença entre o volume de corte e de aterro corrigido mais o valor de Brückner da estaca anterior e assim sucessivamente, conforme abaixo:
\mathrm{B_n=(V_{C,n}-V{Ac,n})+B_{n-1}}
Onde:
- Bn é a ordenada de Brückner na estaca n (m³);
- VC,n é o volume de corte na estaca n (m³);
- VAc,n é o volume de aterro corrigido na estaca n (m³);
- Bn-1 é a ordenada de Brückner na estaca n-1 (m³).
Brückner na estaca 1:
\mathrm{B_1=(376,50-245,65)+5000}
\mathrm{B_{1}=5121,85\:m^3}
Brückner na estaca 2:
\mathrm{B_2=(1064,80-66)+5121,85}
\mathrm{B_{2}=6120,65\:m^3}
Brückner na estaca 3:
\mathrm{B_3=(1420,80-0)+6120,65}
\mathrm{B_{3}=7541,45\:m^3}
Brückner na estaca 4:
\mathrm{B_4=(987,50-35,75)+7541,45}
\mathrm{B_{4}=8493,20\:m^3}
Brückner na estaca 4+8,60 m:
\mathrm{B_4+=(192,43-76,63)+8493,20}
\mathrm{B_{4+}=8609,00\:m^3}
Brückner na estaca 5:
\mathrm{B_5=(51,87-489,37)+8609,00}
\mathrm{B_{5}=8171,50\:m^3}
Brückner na estaca 6:
\mathrm{B_6=(0-1436,60)+8171,50}
\mathrm{B_{6}=6734,90\:m^3}
Brückner na estaca 7:
\mathrm{B_7=(0-1869,34)+6734,90}
\mathrm{B_{7}=4865,56\:m^3}
Brückner na estaca 8:
\mathrm{B_8=(0-1677,06)+4865,56}
\mathrm{B_{8}=3188,50\:m^3}
Brückner na estaca 9:
\mathrm{B_9=(62,50-810,37)+3188,50}
\mathrm{B_{9}=2440,63\:m^3}
Brückner na estaca 9+5,43 m:
\mathrm{B_9+=(24,57-88,44)+2440,63}
\mathrm{B_{9+}=2380,75\:m^3}
Por fim, esse é o resultado final do quadro de volumes de terraplenagem:
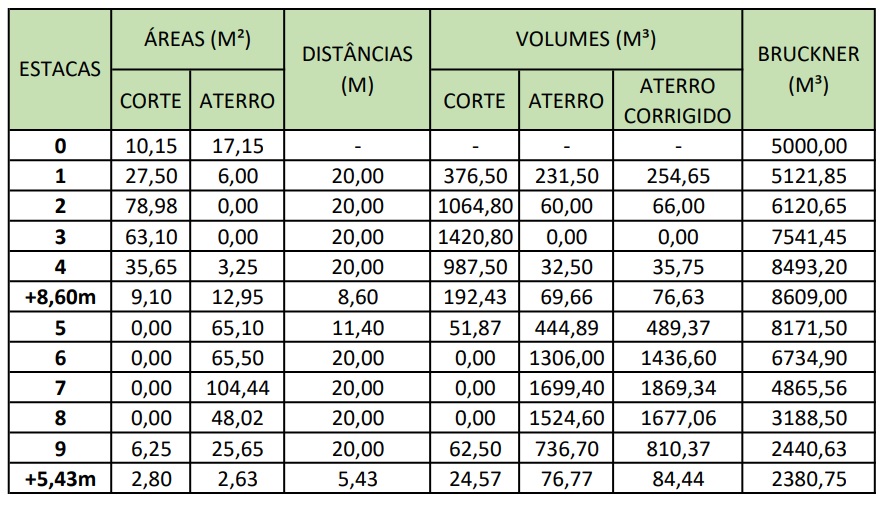
Passo 04: Diagrama de Brückner
Para a construção de uma diagrama de Brückner, basta colocarmos, em um gráfico, as estacas nas abscissas e o Brückner correspondente nas ordenas. Por fim, basta apenas interligarmos cada ponto do gráfico por meio de uma curva, que será chamada de Onda de Brückner.
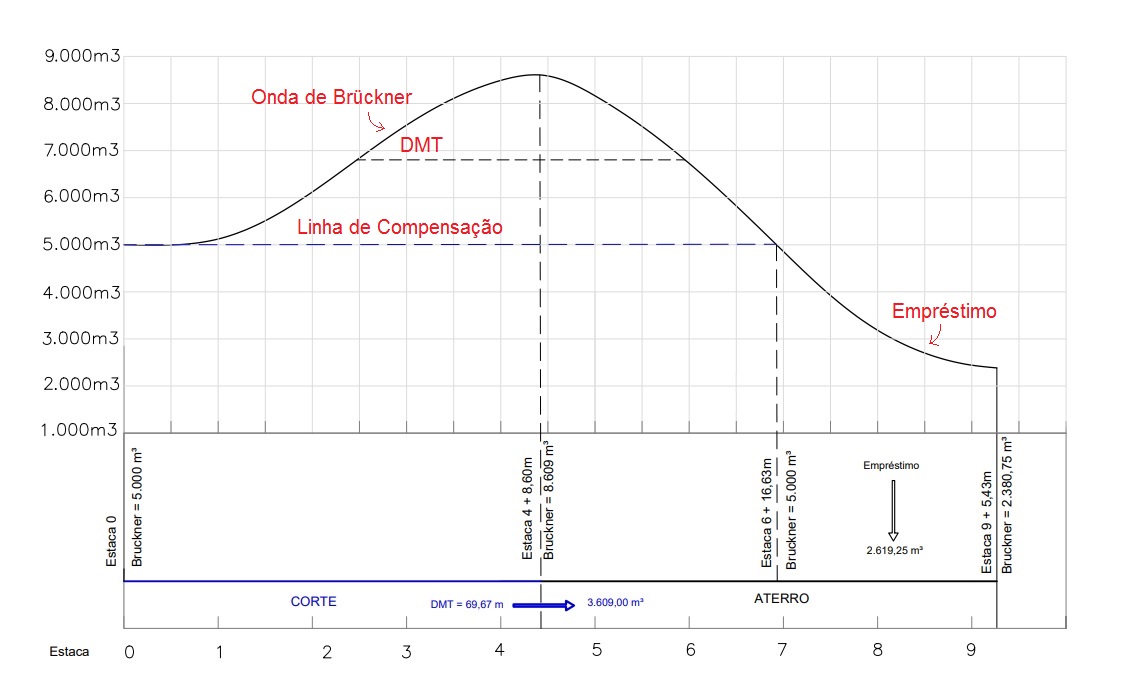
Observe abaixo o diagrama resultante do nosso exemplo:
Como interpretar os resultados do Diagrama de Brückner
Onda de Brückner
Para que possamos interpretar o Diagrama, precisamos saber que os trechos ascendentes da Onda de Brückner representam cortes, e os trechos descendentes, aterros.
Consequentemente, o ponto mais alto (E-4+8,60 m), ou seja, onde a tangente da Onda é zero, é o ponto em que o perfil de projeto coincide com o perfil do terreno e é chamado ponto de passagem de corte para aterro.
Analisando a Onda, é possível também observarmos que a diferença entre as ordenadas de dois pontos representa o volume de terraplenagem entre eles. Podemos perceber isso pelo volume entre a E-0 e a E-4+8,60 de 3609,00 m³, correspondendo justamente ao volume de corte destinado ao preenchimento do aterro.
Linha de compensação
A linha de compensação é uma reta horizontal que intersecciona a onda Brückner em pelo menos dois pontos.
Se a onda fica abaixo da linha de compensação, significa que o volume vai ser transportado no sentido contrário ao estaqueamento (esquerda), caso contrário, será transportado no sentido do estaqueamento (direita).
Distância média de transporte – DMT
É representada pela distância que equivale à base do retângulo de área equivalente ao do trecho compensado e de altura igual à máxima ordenada desse trecho. Na prática, ela representa a distância de transporte de todo o material retirado do corte para a realização do aterro.
Para traçar a DMT é muito simples, basta desenharmos uma linha vertical do ponto de passagem da onda em direção à linha de compensação e desenhar, em seguida, uma linha horizontal que interseccione o ponto médio da linha vertical e a Onda de Brückner.
O tamanho dessa linha horizontal será a DMT, que no nosso caso será 69,67 m.
Empréstimo
É o volume destinado a suprir a carência de material de aterro, que geralmente é extraído da jazida mais próxima a esse aterro.
No Diagrama de Brückner, os empréstimos são representados como linhas descendentes não contempladas pela linha de compensação e seu volume será a diferença entre as ordenadas desses intervalo. No nosso exemplo, o empréstimo necessário será de 2619,25 m³.
Por fim, esperamos que esse post tenha ajudado você a entender como construir e como interpretar um diagrama de Brückner.
Ah, não esquece de conferir o e-Book gratuito sobre Projeto Rodoviário que nós preparamos pra você.
[ebook-projetos-rodoviarios]É claro, no entanto, que esse universo é muito mais amplo do que conseguimos abordar em um e-Book.
Então, se você quiser se especializar nessa área, sugiro que conheça o curso online Formação em Estradas de um dos nosso parceiros, o Grupo HCT, que é um centro de aperfeiçoamento profissional atuante na área tecnológica desde 1997.
Dito isso, ficamos por aqui e se gostou, não deixa de seguir a gente no Instagram e também no Youtube para receber todas as novidades. Até a próxima!.
Fonte:
PONTES FILHO, Glauco. Estradas de rodagem: projeto geométrico. São Carlos: G. Pontes Filho, 1998.
.

Engenheira Civil pela Universidade Federal do Piauí, engenheira de obra, perita judicial e pós-graduanda em Avaliação, Auditoria e Perícias de Engenharia.

Boa tarde. Sugiro corrigir a denominação nos cálculos de volumes de Ac,01 para Vc,01, e também corrigir o resultado de m² para m³, assim sucessivamente em todos os volumes.
Caroline, muito boa a sua observação. Agradecemos muito e iremos corrigir!
porque a seção 2 está com A = 78,98m²??????
Para o cálculo da seção 2, a figura geométrica foi dividida em duas parte para facilitar: um trapézio isósceles de altura de 1,1 m e um triângulo escaleto de altura 7,7 m.