Você sabia que não são apenas as vigas que necessitam de armadura de cisalhamento?
Pois é, existem situações em que precisaremos utilizar armadura de cisalhamento também em lajes.
Assim sendo, nessa publicação você aprenderá, através de um exemplo aplicado, a verificar se sua laje necessita ou não de armadura de cisalhamento.
Lajes sem de cisalhamento
O comportamento das lajes em relação ao esforço cortante difere bastante do apresentado pelas vigas. Por isso, a norma ABNT/NBR: 6118 (2014), diferentemente do colocado para vigas, permite a dispensa de armadura de cisalhamento para lajes, desde que, esforços limites sejam respeitados.
\mathrm{V_{Rd1} = [ \tau_{Rd} \cdot k \cdot \left(1,2 + 40 \cdot \rho_1 \right) + \cdots}
\mathrm{\cdots + 0,15 \cdot \sigma_{cp} ] \cdot b_w \cdot d}
Dessa forma, para a dispensa da armadura de cisalhamento será necessário que \mathrm{V_{Sd} \leq V_{Rd1}}.
Onde:
\mathrm{\tau_{Rd} = 0,25 \cdot f_{ctd}} \mathrm{\rho_1 = \dfrac{A_{s1}}{b_w \cdot d} \leq 0,02} \mathrm{A_{s1}} é a área de armadura tracionada que se estende altura útil mais comprimento de ancoragem necessário além da seção analisada. \mathrm{\sigma_{cp} = \dfrac{N_{Sd}}{A_c}}, no caso da existência de esforço normal. \mathrm{k = 1} para elementos onde 50% da armadura inferior não chega ao apoio. \mathrm{k = 1,6-d} para os demais casos, com d em metros.Desenvolvendo o valor de \mathrm{\tau_{Rd}}, para \mathrm{\gamma_c = 1,4} e concreto de até 50 MPa:
\mathrm{\tau_{Rd} = 0,25 \cdot \dfrac{f_{ctk,inf}}{\gamma_c} = 0,25 \cdot \dfrac{0,7 \cdot f_{ctm}}{\gamma_c}}
\mathrm{\tau_{Rd} = 0,25 \cdot \dfrac{0,7 \cdot 0,3 \cdot f_{ck} ^\frac{2}{3}}{1,4} = 0,0375 \cdot f_{ck} ^\frac{2}{3}}
Além disso, a norma ainda nos permite verificar realizada em uma seção a uma distância d da face do apoio, conforme ilustra a figura abaixo:
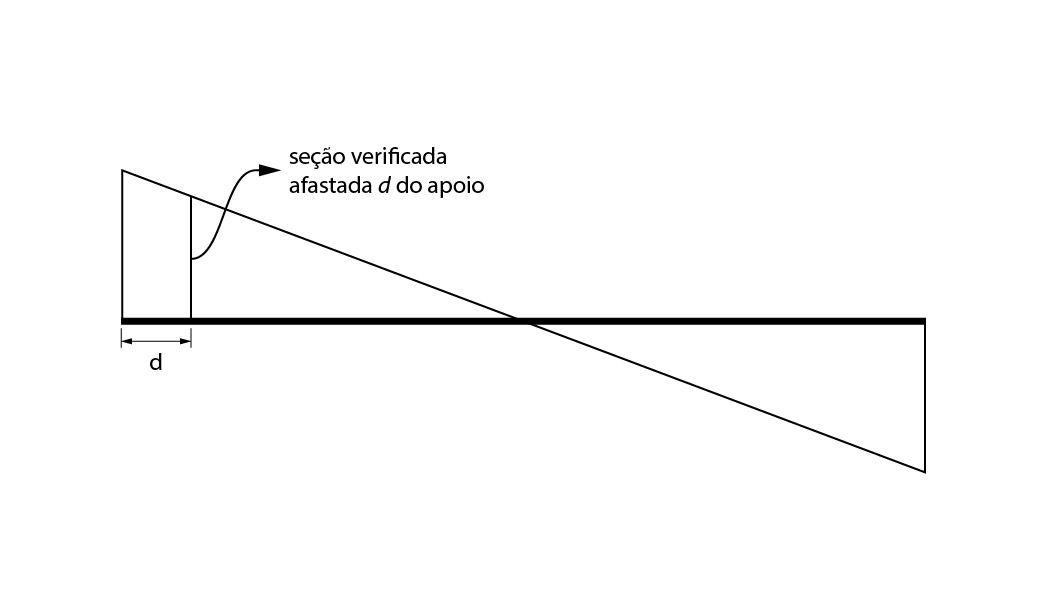
Lajes com armadura de cisalhamento
Em contrapartida, para as lajes em que a condição acima não for satisfeita, é necessário adicionar armaduras transversais para resistir aos esforços cortantes.
As verificações e o dimensionamento serão feitos da mesma forma que as verificações de cisalhamento em vigas.
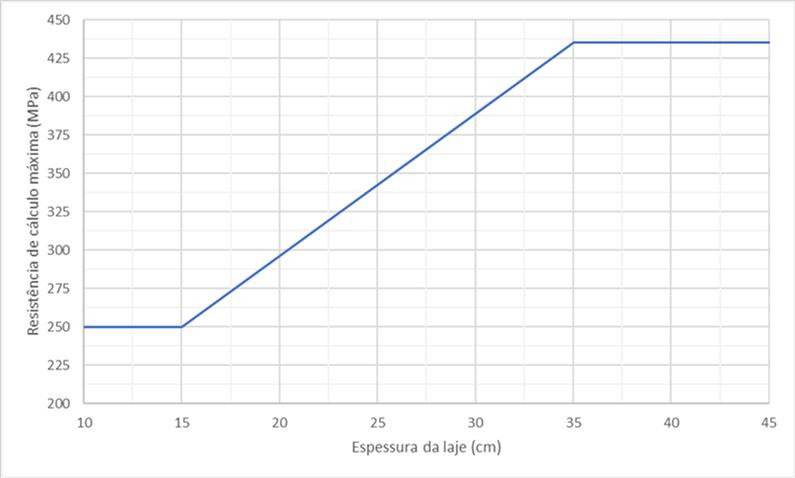
Um detalhe que devemos observar é que a norma restringe a resistência de cálculo da armadura transversal de acordo com a espessura da laje:
- 250 MPa, para lajes com espessura de até 15 cm;
- 435 MPa, para lajes com espessura maior que 35 cm.
No demais casos, a norma permite que interpolemos linearmente. A fim de melhorar o entendimento, preparamos um gráfico combinando resistência de cálculo máxima com a espessura da laje:
Tipo de armadura de cisalhamento em lajes
Quando tratamos de armaduras de cisalhamento em lajes, a facilidade de execução, de modo a não impossibilitar o posicionamento das armaduras de flexão, muitas vezes é um empecilho para diversas das soluções apresentadas. Ainda assim, temos algumas possíveis alternativas para essa armadura.
Algumas dessas alternativas são: estribos fechados simples e duplos, ganchos isolados e conectores de cisalhamento. A figura abaixo apresenta essas soluções:
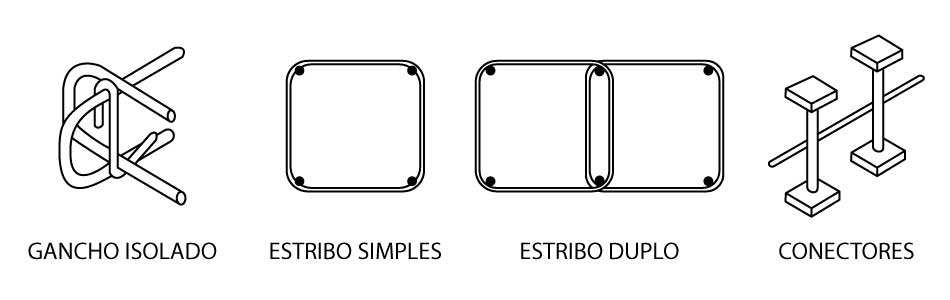
Uma vez que já foi apresentado anteriormente o cálculo da área de aço para vigas, não senti necessidade de repetir as formulações aqui.
Exemplo aplicado de cisalhamento em lajes
Com a finalidade de colocarmos em prática o que aprendemos aqui, vamos verificar a necessidade de armadura de cisalhamento de uma laje de 4,0 m x 5,0 m e 10 cm de espessura, solicitada por um carregamento acidental de 1,5 kN/m² e um revestimento de 1,0 kN/m².
Para essa laje vamos considerar concreto C20 e altura útil de 7,5 cm.
Carregamento atuante
O peso próprio é calculado apenas multiplicando a espessura da laje pelo peso específico do concreto:
\mathrm{g_1=0,1 \cdot 25 = 2,5 \; kN / m^2}
Com isso, o carregamento atuante na laje é:
\mathrm{p= g_1 + g_2 + q =5 \; kN / m^2}
Cálculo do cortante solicitante
Podemos distribuir as cargas entre as vigas por áreas de influência (quinhões de carga):
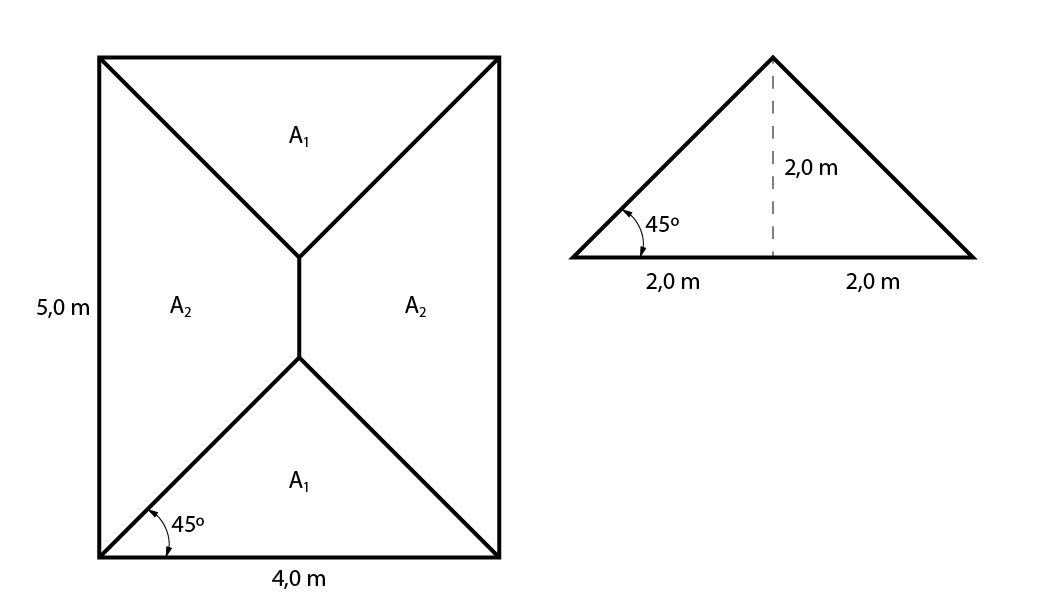
\mathrm{A_1 = \dfrac{4 \cdot 2}{2} = 4,0 \; m^2}
\mathrm{A_T = 2 \cdot A_1 + 2 \cdot A_2}
\mathrm{4 \cdot 5 = 2 \cdot 4 + 2 \cdot A_2}
\mathrm{A_2 = 6,0 \; m^2}
Dessa maneira, o carregamento distribuído na viga, que equivale ao esforço cortante na laje, vale:
\mathrm{V_y = \dfrac{A_1 \cdot p}{l_x}}
\mathrm{V_y = \dfrac{4 \cdot 5}{4} = 5 \; kN / m}
\mathrm{V_x = \dfrac{A_2 \cdot p}{l_y}}
\mathrm{V_x = \dfrac{6 \cdot 5}{5} = 6 \; kN / m}
Dessa forma, a distribuição de esforços cortantes na laje em questão fica:
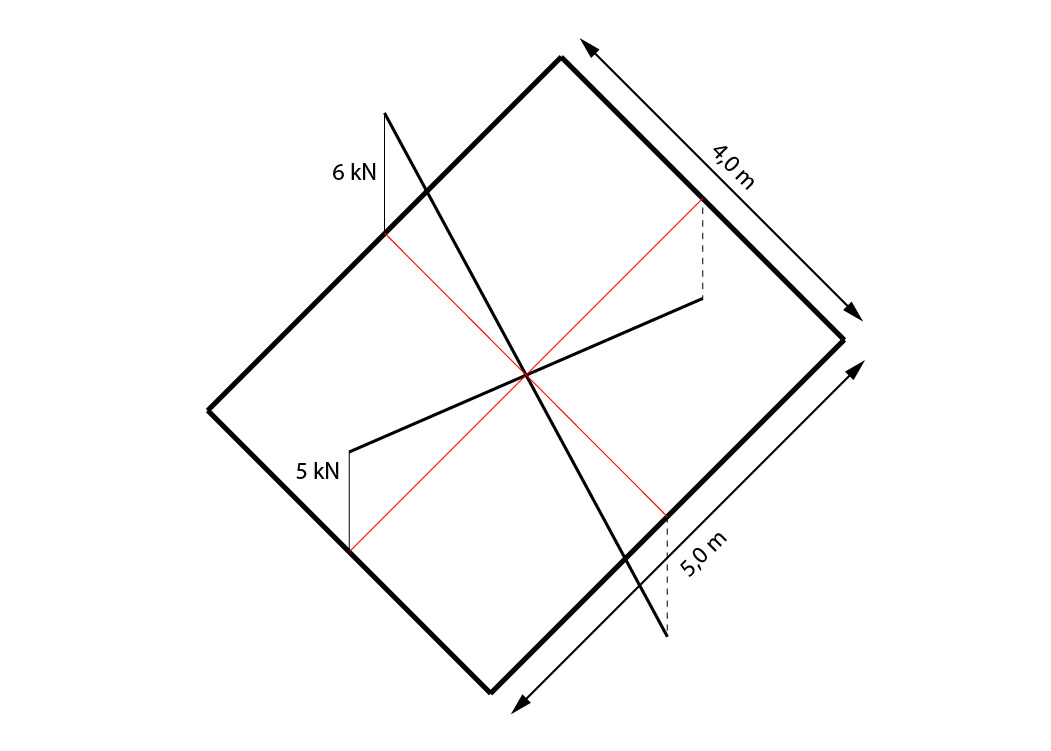
Portanto, o valor do esforço cortante máximo de cálculo vale:
\mathrm{V_{Sd} = 6 \cdot 1,4 = 8,4 \; kN / m}
Cálculo da armadura de flexão atuante
O momento fletor máximo atuante na laje foi calculado através de métodos simplificados e vale \mathrm{M_k = 4,88 \; kN \cdot m /m}.
Com esse valor, podemos calcular a área de aço necessária com utilização da nossa Calculadora de Vigas disponibilizada aqui no site ou simplesmente dimensionarmos manualmente como uma viga de 100 cm de largura por 7,5 cm de altura útil.

Como resultado de 2,21 cm²/m de área necessária, utilizaremos barras de 8 mm a cada 20 cm, o que equivale a 2,5 cm²/m.
Cálculo do cortante resistente
Antes de tudo, vamos repetir o cortante resistente apresentado na teoria:
\mathrm{V_{Rd1} = [ \tau_{Rd} \cdot k \cdot \left(1,2 + 40 \cdot \rho_1 \right) + \cdots}
\mathrm{\cdots + 0,15 \cdot \sigma_{cp} ] \cdot b_w \cdot d}
Em segundo lugar, vamos calcular a tensão de cisalhamento resistente de cálculo:
\mathrm{\tau_{Rd} = 0,0375 \cdot \dfrac{f_{ck} ^ \frac{2}{3}}{10} = 0,0375 \cdot \dfrac{20 ^ \frac{2}{3}}{10}}
\mathrm{\tau_{Rd} = 0,028 \; kN / cm^2}
Com a finalidade de calcular o valor \mathrm{k}, consideraremos que toda a armadura chegará até o apoio. Assim sendo, teremos:
\mathrm{k = 1,6 - d}
\mathrm{k = 1,6 - 0,075 = 1,525}
Sabendo que a área de aço tracionada é 2,5 cm²:
\mathrm{\rho_1 = \dfrac{A_{s1}}{b_w \cdot d}}
\mathrm{\rho_1 = \dfrac{2,5}{100 \cdot 7,5}=0,00333}
Visto que o esforço normal é nulo, \mathrm{\sigma_{cp} = 0}.
\mathrm{V_{Rd1} = [ 0,028 \cdot 1,525 \cdot (1,2 + \cdots}
\mathrm{\cdots + 40 \cdot 0,00333 ) + 0,15 \cdot 0 ] \cdot 100 \cdot 7,5}
\mathrm{V_{Rd1}= 42,7 \; kN}
Por fim, comparando o esforço cortante solicitante com o resistente:
\mathrm{V_{Sd} = 8,4 \leq 42,7}
Sendo assim, a laje estudada dispensa armadura de cisalhamento.
Recado final
No caso de lajes maciças, usualmente, as mesmas dispensam a armadura de cisalhamento. Só para exemplificar, vamos tomar como exemplo a nossa laje estudada: mesmo que aumentássemos o carregamento, a laje provavelmente apresentaria limitações de deformação excessiva antes de apresentar problemas de cisalhamento.
Seja como for, a verificação de cisalhamento em lajes é obrigatória em todos os projetos. Assim sendo, uma forma de verificarmos o cisalhamento em lajes em projetos feitos à mão, é encontrarmos o maior contante de laje em todo o edifício e verificarmos uma única vez.
Gostaria de ter acesso a um curso sobre modelagem de alvenaria estrutural no Revit?
Aproveite enquanto está com um preço especial.

E se você necessário calcular a verficação da laje, como seria seu cálculo e seu detalhamento?
Não entendi bem a pergunta, Letícia.
A verificação do cisalhamento é o apresentado no post.
Quanto ao detalhamento realmente ficou faltando.
Fica para uma publicação futura, obrigado pela sugestão!
Abraço!
Me expressei mal, se fosse necessário a armadura de cisalhamento, como seria seu cálculo?Obrigada!
Geralmente letícia não se utiliza armaduras de cisalhamento em lajes, o que costuma ser feito é a modificação da seção ( aumentar as dimenções ), afim proporcionar uma resistência suficente.