Ao tratar de estruturas de concreto armado, é importante percebermos que após dimensionarmos corretamente as áreas de aço necessárias para cada situação, é necessário também transmitirmos esses esforços ao concreto, fato que chamamos de ancoragem.
Nessa publicação você aprenderá os conceitos de ancoragem, assim como o cálculo do comprimento necessário para a mesma.
Caso queira ver um exercício aplicado de ancoragem em vigas, basta ver o vídeo abaixo:
Comprimento básico de ancoragem
Existem algumas formas de realizar a ancoragem de barras de aço. Entre elas podemos destacar a ancoragem apenas pela aderência entre aço e concreto e também a ancoragem pela utilização de dispositivos especial.
Uma vez que a utilização de ancoragem por aderência são economicamente mais atraentes e portanto mais utilizadas, focaremos na mesma nessa publicação.
Para iniciar o nosso estudo, vamos considerar uma barra de aço inserida em um bloco de concreto e submetida a uma força \mathrm{R_d}.
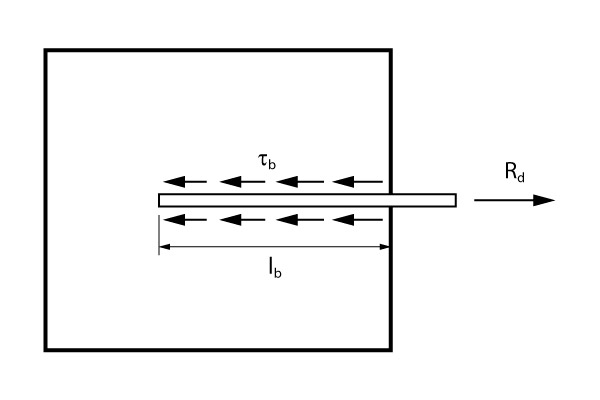
A aderência entre o concreto e o aço gera tensões \mathrm{\tau_b}. Apesar dessas tensões variarem ao longo da barra, utilizaremos um valor de tensão média \mathrm{f_{bd}}.
A força na barra pode ser escrita em função da área da tensão atuante na mesma e da sua área de seção transversal.
\mathrm{R_d = A_s \cdot f_{yd}}
\mathrm{R_d = \dfrac{\pi \cdot \phi ^2}{4} \cdot f_{yd}}
A força resultante das tensões tangências pode ser calculada pelo produto da área superficial da barra (onde a tensão atua) e o valor da tensão média.
\mathrm{F = A_{superficial} \cdot f_{bd}}
\mathrm{F = \pi \cdot \phi \cdot lb \cdot f_{bd}}
Temos que a força aplicada na barra deve ser equilibrada pela força resultante das tensões tangenciais:
\mathrm{F = R_d}
\mathrm{\pi \cdot \phi \cdot lb \cdot f_{bd} = \dfrac{\pi \cdot \phi ^2}{4} \cdot f_{yd}}
Com isso chegamos no comprimento básico de ancoragem:
\mathrm{l_b = \dfrac{\phi}{4} \cdot \dfrac{f_{yd}}{f_{bd}}}
Tensão de aderência de cálculo
Vamos focar agora na obtenção da tensão de aderência de cálculo, \mathrm{f_{bd}}, uma vez que todos os outros termos já são conhecidos. Para obtenção do mesmo, utilizaremos a seguinte fórmula da norma ABNT/NBR: 6118 (2014):
\mathrm{f_{bd} = \eta_1 \cdot \eta_2 \cdot \eta_3 \cdot f_{ctd}}
Agora vamos abordar cada elemento presente nessa igualdade.
Fator \mathrm{\eta_1}
O primeiro fator irá variar de acordo com o tipo de aço utilizado:
- \mathrm{\eta_1 = 1,0} no caso de barras lisas como CA25 e CA60 liso;
- \mathrm{\eta_1 = 1,4} no caso de barras entalhadas como CA60 entalhado;
- e \mathrm{\eta_1 = 2,25} no caso de barras nervuradas como CA50 e CA60 nervurado.
Fator \mathrm{\eta_2}
O próximo fator está relacionado diretamente com o conceito de regiões de boa e má aderência.
De acordo com a norma, as regiões de boa aderência são os trechos das barras que possuem uma inclinação superior a 45º em relação a horizontal e no caso de trechos horizontais ou com inclinação inferior a 45º nos casos:
- elementos com altura inferior a 60 cm e que as barras estejam no máximo 30 cm acima da face inferior (ou junta de concretamente mais próxima);
- elementos com igual ou superior a 60 cm e que as barras estejam no mínimo 30 cm acima da face superior (ou junta de concretamente mais próxima).
A imagem abaixo apresenta nas regiões hachuradas as regiões consideradas como boa aderência.
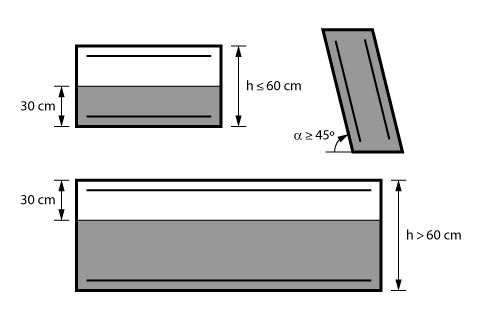
Os demais trechos podem ser considerados como de má aderência.
Uma vez determinada de qual região se trata, podemos obter os fatores:
- \mathrm{\eta_2 = 1,0} para regiões de boa aderência;
- \mathrm{\eta_2 = 0,7} para regiões de má aderência.
Fator \mathrm{\eta_3}
O último fator trazido pela norma leva em consideração apenas o diâmetro da barra que estamos ancorando. No caso de barras de diâmetro inferior a 32 mm teremos \mathrm{\eta_3 = 1,0}. Para os demais casos:
\mathrm{\eta_3 = \dfrac{132 - \phi}{100}} com o diâmetro entrando em mm.Em linhas gerais, teremos esse fator como 1,0, uma vez que raramente utilizaremos barras superior a 32 mm em obras usuais.
Valor de cálculo da resistência a tração do concreto
Para a verificação da ancoragem, o valor de cálculo \mathrm{f_{ctd}} deve ser obtido a partir da resistência característica inferior do concreto à tração \mathrm{f_{ctk,inf}}.
\mathrm{f_{ctd} = \dfrac{f_{ctk,inf}}{\gamma_c}}
A resistência característica inferior do concreto à tração vale 70% da resistência característica média \mathrm{f_{ctm}}, que por sua vez vale:
\mathrm{f_{ctm} = 0,3 \cdot f_{ck} ^{\frac{2}{3}}} para concretos de resistência característica até 50 MPa e;
\mathrm{f_{ctm} = 2,12 \cdot ln \left( 1 + 0,11 \cdot f_{ck} \right)} para concretos de resistência característica acima de 50 MPa.
A partir desse ponto, seguiremos com dedução para concretos de classe até C50. Dessa forma, podemos calcular o \mathrm{f_{ctk,inf}}:
\mathrm{f_{ctk,inf} = 0,7 \cdot f_{ctm}}
\mathrm{f_{ctk,inf} = 0,21 \cdot f_{ck} ^{\frac{2}{3}}}
E considerando o \mathrm{\gamma_c = 1,4}, podemos simplificar a formulação para o \mathrm{f_{ctd}}:
\mathrm{f_{ctd} = \dfrac{f_{ctk,inf}}{\gamma_c}}
\mathrm{f_{ctd} = \dfrac{0,21 \cdot f_{ck} ^{\frac{2}{3}}}{1,4} = 0,15 \cdot f_{ck} ^{\frac{2}{3}}}
Por fim, agora já conhecemos todos os termos para o cálculo de \mathrm{f_{bd}}.
Comprimento de ancoragem necessário
Nesse momento, é importante perceber que usualmente utilizamos áreas de aço superiores aquela calculada. Uma forma de levar isso em consideração é calcular o comprimento de ancoragem necessário multiplicando o comprimento básico de ancoragem pela razão entre essas duas áreas de aço:
\mathrm{l_{b,nec} \geq l_b \cdot \dfrac{A_{s,calc}}{A_{s,ef}}}
Vamos entrar em cada um desses termos agora:
- \mathrm{l_b} já aprendemos a calcular, e de acordo com a última edição da norma brasileira ele deve ser superior a \mathrm{25 \cdot \phi};
- por último temos a razão entre a área de aço calculada e a área de aço que realmente utilizamos na ancoragem.
O \mathrm{l_{b,nec}} em todas as situações deverá ser superior ao \mathrm{l_{b,mín}}:
\mathrm { l_{b,mín} \geq \left\{ \begin{array}{ll} 0,3 \cdot l_b \\ 10 \cdot \phi \\ 10 \; cm \end{array} \right. }
Barras com gancho na extremidade
Podemos reduzir ainda mais o comprimento de ancoragem necessário utilizando ganchos nas extremidades da barra. Dessa forma, podemos generalizar mais a formulação apresentada acima de modo a incluir a utilização ou não de ganchos:
\mathrm{l_{b,nec} \geq \alpha_1 \cdot l_b \cdot \dfrac{A_{s,calc}}{A_{s,ef}}}
Onde \mathrm{\alpha_1} será igual a 1,0 caso a ancoragem seja reta ou com ganchos com o cobrimento inferior a \mathrm{3 \cdot \phi} e será igual a 0,7 no caso da utilização de ganchos com cobrimento no mínimo igual a \mathrm{3 \cdot \phi}.
A norma brasileira apresenta alguns comprimentos mínimos para as extremidades retas desses ganchos de acordo com sua tipologia:
- prolongamento de \mathrm{2 \cdot \phi} para ganchos semicirculares;
- \mathrm{4 \cdot \phi} para ganchos em 45º;
- e prolongamento de \mathrm{8 \cdot \phi} para ganchos em ângulo reto.
A imagem abaixo resume essas dimensões:
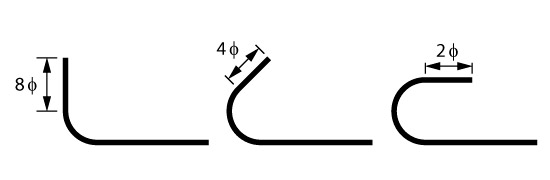
Além desse comprimento reto, também encontramos na norma os diâmetros mínimos dos pinos de dobrando para formar os ganchos em função da bitola da barra e do tipo de aço utilizado:
| Bitola | CA25 | CA50 | CA60 |
| \mathrm{\phi < 20} | \mathrm{4 \cdot \phi} | \mathrm{5 \cdot \phi} | \mathrm{6 \cdot \phi} |
| \mathrm{\phi \geq 20} | \mathrm{5 \cdot \phi} | \mathrm{8 \cdot \phi} |
Ancoragem em apoios
Nesse tópico vamos verificar as disposições da norma para a ancoragem em apoios, sejam eles intermediários ou de extremidade.
As barras em uma apoio de extremidade devem ser capazes de ancorar uma força de:
\mathrm{R_{Sd} = \dfrac{a_l}{d} \cdot V_{Sd}}
O valor de \mathrm{a_l} é o mesmo que já utilizamos em publicações anteriores relativo ao deslocamento do diagrama de momentos fletores e o \mathrm{V_{Sd}} equivale ao esforço cortante de cálculo naquele apoio.
Com a força já calculada, podemos obter a área de aço necessária no apoio apenas considerando que a mesma está escoando:
\mathrm{A_s = \dfrac{R_{Sd}}{f_{yd}} }
No caso de ancoragem em apoios de extremidade com a utilização de ganchos o valor de \mathrm{l_{b,nec}} também deve ser superior a:
\mathrm { l_{b,nec} \geq \left\{ \begin{array}{ll} R + 5,5 \cdot \phi \\ 6 \; cm \end{array} \right. }
Em que podemos tirar o valor de R do diâmetro do pino de dobramento apresentado na tabela acima.
Além da área calculada anteriormente, tanto no caso de apoios de extremidade quanto nos apoios intermediários devemos:
- utilizar pelo menos 1/3 da área de aço do vão, caso o momento no apoio seja nulo ou inferior a 50% do momento no vão;
- ou utilizar pelo menos 1/4 da área de aço do vão, caso o momento no apoio seja superior a 50% do momento no vão.
No caso de apoios intermediários que não haja possibilidade de ocorrência de momentos fletores positivos, o comprimento de ancoragem pode ser igual a \mathrm{10 \cdot \phi}. Nesta situação, é recomendado utilizar uma barra contínua ou realizar uma emenda adequada na região.
Utilização de grampos
Vamos imaginar agora a situação em que temos um comprimento disponível para ancoragem das barras de uma viga dentro de um pilar inferior ao comprimento de ancoragem necessário. Nessa situação, podemos prosseguir de duas formas:
- caso não estejamos levando todas as barras do meio do vão para o apoio, podemos fazer assim. O motivo é aumentar a área de aço efetiva, diminuindo assim o comprimento de ancoragem necessário;
- na situação em que todas as barras já estão indo até o apoio podemos complementar essa armação com grampos horizontais.
Podemos calcular a área de aço necessária nesses grampos pela formulação abaixo:
\mathrm{A_{grampo} = \dfrac{R_{sd}}{f_{yd}} \cdot \left( 1 - \dfrac{l_{b,disp}}{l_{b,nec}} \right)}
Para o comprimento dos grampos, podemos utilizar o comprimento básico de ancoragem levando em consideração o diâmetro das barras do grampo. Vamos avançar esse comprimento a partir da face de apoio.
Recado final
Agora eu espero que você já tenha aprendido sobre ancoragem em barras de aço. Para complementar essa publicação vamos estudar em posts futuros sobre emendas de barras de aço, assim como a resolução de exercícios.
Caso esse conteúdo tenha sido útil para você, compartilhe com um amigo que você acredita que também tem interesse.
Fonte:
ARAÚJO, J. M. Curso de Concreto Armado. Rio Grande: Editora Dunas, 2014. v. 1
ASSOCIAÇÃO BRASILEIRA DE NORMAS TÉCNICAS. NBR 6118: Projeto de estruturas de concreto – Procedimento. Rio de Janeiro, 2014.
Gostaria de ter acesso a um curso sobre modelagem de alvenaria estrutural no Revit?
Aproveite enquanto está com um preço especial.
