Ancoragem da armadura no concreto: exercício resolvido

Nesse post nós vamos resolver um exercício completo sobre ancoragem de armaduras no concreto. Como aqui focaremos apenas na resolução do problema, recomendo que confira a publicação que citei anteriormente, em que apresento a teoria e as considerações de norma sobre o assunto.

Apresentação do problema

Para aplicarmos esse conteúdo eu selecionei um viga já utilizada como exemplo aqui no blog. A mesmo foi utilizada para estudarmos sobre decalagem em vigas de concreto armado. Apenas para facilitar, vou repetir aqui a situação que iremos resolver. É importante que você veja a resolução do exemplo de decalagem em vigas porque utilizaremos os comprimentos já decalados para chegar ao comprimento total da barra.

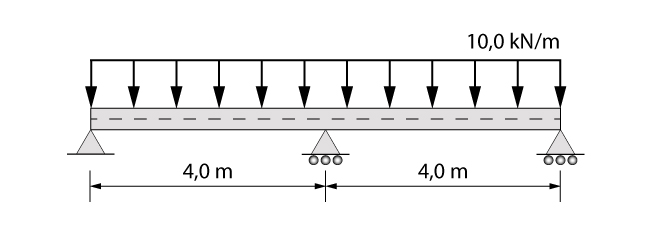
A viga em questão tem 14 cm de largura por 30 cm de altura, 27,5 cm de altura útil e utiliza concreto classe C20 e aço CA-50.

Além desses valores, será necessário adicionar mais uma informação aqui, que é a largura dos apoios. No nosso caso, consideraremos que os pilares possuem 20 cm na direção da viga.

Antes de partirmos para essa resolução, caso você prefira acompanhar o conteúdo por vídeo, basta clicar no vídeo abaixo:

Resultados já obtidos

No dimensionamento da armadura longitudinal dessa viga, obtivemos 1,42 cm² para a armadura positiva e com isso utilizamos 3 barras de 8 mm e chegamos em 2,67 cm² para armadura negativa sob o apoio intermediário e utilizamos 4 barras de 10 mm.

Nós chegamos nessa área de aço utilizando a Calculadora de Vigas gratuita aqui do blog. Caso queira receber a sua também basta informar o e-mail no formulário abaixo.

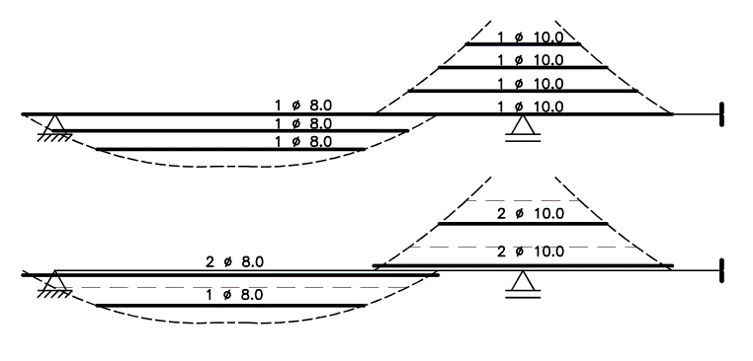
[formulario-calculadora-flexao]

A imagem a seguir, apresenta o resultado da decalagem tanto para o momento positivo quanto para o momento negativo.

Comprimento básico de ancoragem

O primeiro passo para analisarmos os comprimentos de ancoragem é o cálculo do comprimento básico de ancoragem. Para isso, vamos calcular inicialmente a tensão média de aderência entre o aço e o concreto.

\mathrm{f_{bd} = \eta_1 \cdot \eta_2 \cdot \eta_3 \cdot f_{ctd}}

A resistência a tração do concreto, no caso de concretos até 50 MPa e considerando o \mathrm{\gamma_c = 1,4} pode ser calculada pela fórmula abaixo:

\mathrm{f_{ctd} = 0,15 \cdot f_{ck} ^{\frac{2}{3}}}

\mathrm{f_{ctd} = 0,15 \cdot 20 ^{\frac{2}{3}} = 1,11 \; MPa}

Como no caso estamos utilizando barras de CA-50 com diâmetro inferior a 32 mm, utilizaremos \mathrm{\eta_1 = 2,25} e \mathrm{\eta_3 = 1,0}.

Para o valor de \mathrm{\eta_2}, temos que lembrar que para uma viga inferior a 60 cm, os primeiros 30 cm são considerados de boa aderência.

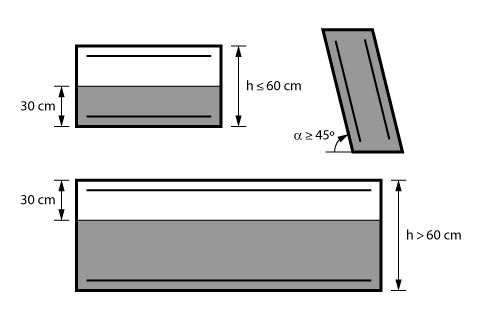
Como no nosso caso a viga é inferior a 60 cm e tem apenas 30 cm, ela por inteira será considerada uma região de boa aderência. Dessa forma, teremos \mathrm{\eta_2 = 1,0}.

Podemos então calcular o valor de \mathrm{f_{bd}}:

\mathrm{f_{bd} = \eta_1 \cdot \eta_2 \cdot \eta_3 \cdot f_{ctd}}

\mathrm{f_{bd} = 2,25 \cdot 1,0 \cdot 1,0 \cdot 1,11 = 2,49 \; MPa}

Agora vamos para o cálculo do comprimento básico de ancoragem:

\mathrm{l_b = \dfrac{\phi}{4} \cdot \dfrac{f_{yd}}{f_{bd}}}

\mathrm{l_b = \dfrac{\phi}{4} \cdot \dfrac{435}{2,49} = 44 \cdot \phi \geq 25 \cdot \phi}

Coloquei o comprimento básico em função do diâmetro da barra devido ao fato de termos diâmetros diferentes para as armaduras positivas e negativas.

Ancoragem da armação positiva decalada

Temos que para o vão positivo, agrupamos a decalagem em dois grupos de barras, 2 barras de 8 mm de um comprimento e 1 barra de 8 mm de outro comprimento. Lembre-se que, apesar do comprimento decalado das duas barras de 8 mm não chegar até o apoio intermediário, temos que levar no mínimo duas barras até os apoios.

Dessa forma, para as duas barras de 8 mm, já temos definido que as mesmas irão de apoio a apoio.

Para a barra de 8 mm isolada, temos que calcular o comprimento de ancoragem necessário:

\mathrm{l_{b,nec} \geq l_b \cdot \dfrac{A_{s,calc}}{A_{s,ef}}}

O valor do mesmo será basicamente o comprimento básico de ancoragem minorado pela razão da área de aço calculada e a área de aço efetiva. Como temos 3 barras de 8 mm, a área de aço efetiva vale 1,5 cm². Assim sendo, o comprimento de ancoragem necessário vale:

\mathrm{l_{b,nec} = 44 \cdot 0,8 \cdot \dfrac{1,42}{1,5} = 33 \; cm}

Comprimento de ancoragem mínimo

É necessário compararmos o valor encontrado com o comprimento de ancoragem mínimo.

\mathrm { l_{b,mín} \geq \left\{ \begin{array}{ll} 0,3 \cdot l_b \\ 10 \cdot \phi \\ 10 \; cm \end{array} \right. }

\mathrm { l_{b,mín} \geq \left\{ \begin{array}{ll} 0,3 \cdot 44 \cdot 0,8 = 10,6 \; cm  \\ 10 \cdot 0,8 = 8 \; cm \\ 10 \; cm \end{array} \right. }

Como o valor encontrado foi superior ao comprimento mínimo, podemos prosseguir com o mesmo.

Com isso podemos acrescentar o valor encontrado para cada direção do barra, conforme apresenta em verde a figura abaixo:

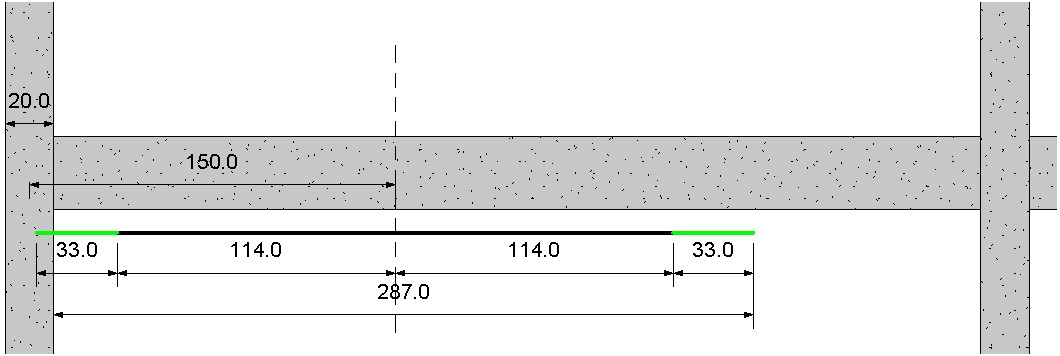
Julgo importante comentarmos os valores apresentados na figura acima. O 150 cm corresponde a distância entre o eixo do pilar (considerando como apoio pontual no modelo de cálculo) até o máximo momento positivo. O valor de 114 cm corresponde a metade do comprimento decalado e assim como os 150 cm, também foi retirado do AutoCAD.

Como ao adicionar os 33 cm na extremidade esquerda da barra chegamos ao apoio de extremidade, iremos levar essa barra também para esse apoio. Logo, teremos 3 barras de 8 mm chegando até o apoio de extremidade.

O valor de 287 cm marca o ponto que podemos interromper a barra de 8 mm que está isolada. Podemos chegar nele também pela simples conta abaixo:

\mathrm{140 + 114 + 33 = 287 \; cm}

Observe que, se temos 150 cm do eixo do apoio até o pico do momento e o apoio tem 20 cm de largura, teremos 140 cm da face do pilar até o pico do momento.

Ancoragem da armadura positiva nos apoios de extremidade

Pensando inicialmente na armadura efetiva, teremos o mesmo valor utilizado anteriormente, uma vez que estamos com as três barras de 8 mm chegando nesse apoio.

Podemos avançar então para o cálculo da área de aço necessária no apoio. A primeira área que vamos calcular é a ancoragem da força \mathrm{R_{sd}}:

\mathrm{A_s = \dfrac{R_{Sd}}{f_{yd}} =\dfrac{a_l}{d} \cdot \dfrac{V_{sd}}{f_{yd}} }

\mathrm{A_{s,apoio} = \dfrac{27,5}{27,5} \cdot \dfrac{21}{43,5} = 0,48 \; cm^2 }

Nessa resolução, não calculamos o momento negativo na ligação da viga com os pilares de extremidade. Vamos considerar aqui que seu valor (em módulo) é inferior a metade do momento positivo. Dessa forma, é necessário termos pelo menos um terço da armadura do vão chegando até o apoio.

\mathrm{A_{s,apoio} = \dfrac{1,5}{3} = 0,50 \; cm^2 }

Entre os dois valores, prosseguiremos com o maior encontrado.

Podemos agora então calcular o \mathrm{l_{b,nec}}:

\mathrm{l_{b,nec} \geq \alpha \cdot l_b \cdot \dfrac{A_{s,calc}}{A_{s,ef}}}

\mathrm{l_{b,nec} = 0,7 \cdot 44 \cdot 0,8 \cdot \dfrac{0,5}{1,5} = 8,16 \; cm}

Repare que utilizamos o valor \mathrm{\alpha = 0,7}, considerando assim que teremos gancho na extremidade.

Comprimento de ancoragem mínimo

Além do \mathrm { l_{b,mín} = 10,6 \; cm} já encontrado, para apoios de extremidade com gancho temos que verificar também os seguintes valores:

\mathrm { l_{b,nec} \geq \left\{ \begin{array}{ll} R + 5,5 \cdot \phi \\ 6 \; cm \end{array} \right. }

\mathrm { l_{b,nec} \geq \left\{ \begin{array}{ll} 2,5 \cdot \phi + 5,5 \cdot \phi = 6,4 \; cm \\ 6 \; cm \end{array} \right. }

Considerando o maior valor encontrado, 10,6 cm, e sabendo que o apoio de 20 cm de largura, observamos possuímos espaço suficiente para ancorar essas barras no apoio.

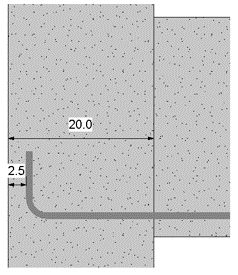
Ancoragem da armadura positiva no apoio intermediário

No apoio intermediário, temos que o momento fletor negativo é superior a metade do momento fletor no meio do vão. Assim sendo, é necessário levar pelo menos um quarto da área de aço até esse apoio.

De qualquer forma, estamos levando a quantidade mínima de duas barras (2/3 da área de aço do vão) até o apoio.

No caso de apoios intermediários em que não existe a possibilidade de ocorrência de momentos fletores positivos, podemos avançar apenas 10 vezes o diâmetro da barra.

\Delta l = \mathrm{10 \cdot \phi}

\Delta l = \mathrm{10 \cdot 0,8 = 8 \; cm}

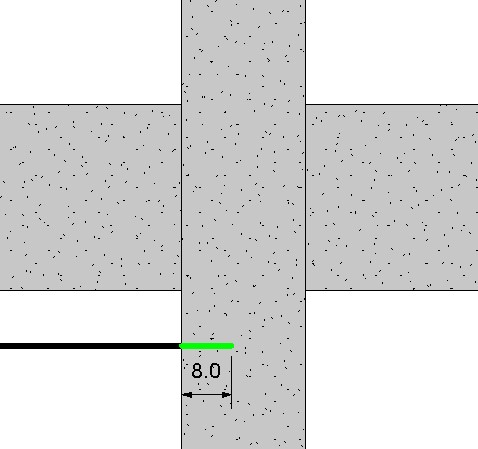
Ancoragem da armação negativa

A área de aço calculada para o momento negativo foi 2,67 cm². Como adotamos 4 barras de 10 mm para a região, a área de aço efetiva vale 3,2 cm². Assim sendo, podemos calcular o comprimento de ancoragem necessário:

\mathrm{l_{b,nec} \geq l_b \cdot \dfrac{A_{s,calc}}{A_{s,ef}}}

\mathrm{l_{b,nec} \geq 44 \cdot 1,0 \cdot \dfrac{2,67}{3,2} = 37 \; cm}

É necessário compararmos o valor encontrado com o comprimento de ancoragem mínimo.

\mathrm { l_{b,mín} \geq \left\{ \begin{array}{ll} 0,3 \cdot l_b \\ 10 \cdot \phi \\ 10 \; cm \end{array} \right. }

\mathrm { l_{b,mín} \geq \left\{ \begin{array}{ll} 13,1 \; cm  \\ 10 \; cm \\ 10 \; cm \end{array} \right. }

Podemos obter o comprimento decalado tanto através de uma cota direta no AutoCAD como através de uma equação dos momentos fletores. Aqui seguiremos com a primeira opção:

Assim sendo, vamos prolongar 37 cm para cada direção nos dois grupos de ferro, chegando no comprimento total do ferro negativo:

\mathrm { l_1 = 2 \cdot \left( 71+37 \right) = 216 \; cm}

\mathrm { l_2 = 2 \cdot \left( 128+37 \right) = 330 \; cm}

Detalhamento final

A fim de chegarmos no detalhamento final, só falta calcularmos o comprimento da parte reta dos ganchos. No caso de ganchos retos, esse valor deve ser \mathrm {8 \cdot \phi = 6,4 \; cm}. Utilizaremos no detalhamento o valor de 10 cm.

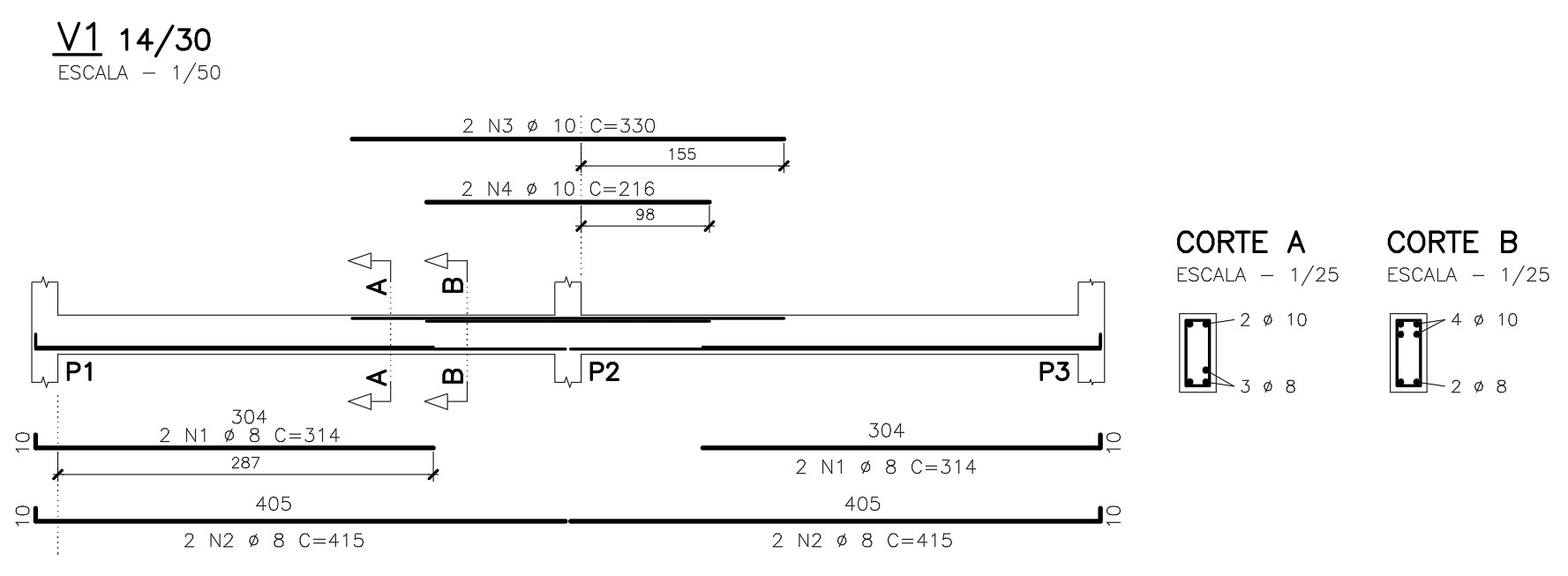
Recado final

Agora que você já conferiu a teoria e um exemplo prático de aplicação, nós fechamos o conteúdo de ancoragem em barras de concreto. Saiba que essa seção de comentários e o nosso YouTube estão sempre abertos para questionamentos sobre assuntos de engenharia.

---

Fonte:

ARAÚJO, J. M. Curso de Concreto Armado. Rio Grande: Editora Dunas, 2014. v. 1

ARAÚJO, J. M. Curso de Concreto Armado. Rio Grande: Editora Dunas, 2014. v. 2

ASSOCIAÇÃO BRASILEIRA DE NORMAS TÉCNICAS. NBR 6118: Projeto de estruturas de concreto – Procedimento. Rio de Janeiro, 2014.

CARVALHO, R. C.; FIGUEIREDO FILHO, J. R. Cálculo e Detalhamento de Estruturas Usuais de Concreto Armado Segundo a NBR 6118:2014. São Carlos: EdUFSCar, 2014.