Uma das etapas que geram bastante dúvidas durante o detalhamento de vigas de concreto é a etapa da decalagem, em que o modelo de cálculo utilizado até então (equilíbrio da seção) é corrigido. Mas não se preocupe, nesse post você vai aprender de uma vez por todas o necessário para realizar a decalagem.
O que você irá encontrar nesse post:
- o porquê de fazermos a decalagem;
- as considerações da norma sobre o assunto;
- um exemplo prático da aplicação da decalagem.
Antes de partimos para o conteúdo, caso você prefira aprender decalagem através de vídeo, basta conferir abaixo!
Introdução
É importante lembrar que as formulações utilizadas no dimensionamento de vigas de concreto foram obtidas considerando as vigas submetidas à flexão pura, ou seja, sem existência de cisalhamento. Esta consideração não é muito usual, uma vez que, em situações usuais, as vigas estarão submetidas também a cisalhamento.
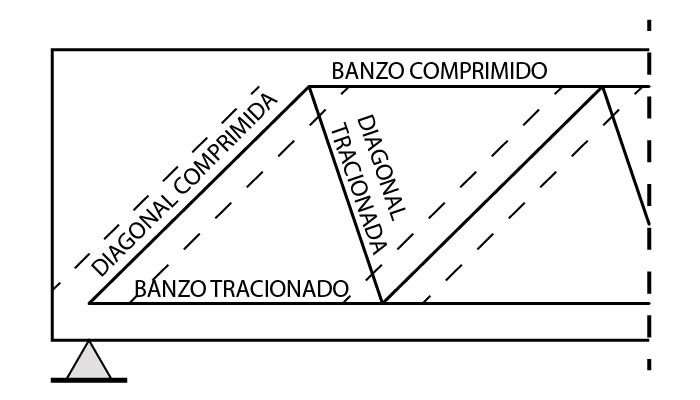
A fim de considerar o efeito do cisalhamento, vamos utilizar as mesmas considerações realizadas nas verificações de vigas submetidas à cisalhamento. Ou seja, utilizaremos um modelo que representa a viga de concreto a partir de uma treliça, denominada treliça de Mörsch, ilustrada na figura abaixo.
Por que fazemos decalagem?
Inicialmente, é importante revisarmos como o modelo de treliça representa uma viga de concreto. Veja abaixo o que cada elemento da treliça simula em uma viga de concreto:
a) o banzo tracionado representa a armadura longitudinal;
b) o banzo comprimido simula o concreto comprimido;
c) a diagonal comprimida representa a biela inclinada;
d) a diagonal tracionada (usualmente disposta na vertical) representa a armadura transversal.
Agora que já entendemos o que cada elemento representa, vamos analisar a extremidade esquerda de uma viga hipotética através de uma treliça.
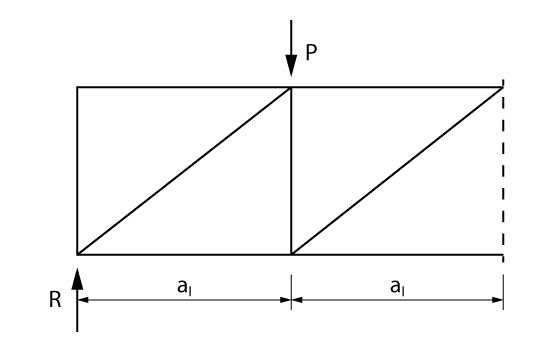
Agora vamos seccionar a treliça a partir de uma seção SS, em que obteremos a tração na armadura \mathrm{F_{s,B}} no ponto B e a compressão no concreto no \mathrm{F_c} no ponto A.

Realizando agora o equilíbrio de momento no ponto A, teremos:
\mathrm{R \cdot 2 \cdot a_l - P \cdot a_l - F_{s,B} \cdot Z=0}
Onde \mathrm{Z} é o braço de alavanca, distância entre o banzo tracionado e o banzo comprimido.
Repare que a parcela \mathrm{R \cdot 2 \cdot a_l - P \cdot a_l} representa o momento fletor na seção em que o ponto A se localiza.
\mathrm{M_{d,A} - F_{s,B} \cdot Z}
\mathrm{F_{s,B} = \dfrac{M_{d,A}}{Z}}
O mais importante de repararmos aqui é que a tração na armadura no ponto B está sendo calculada em uma seção deslocada (mais solicitada), no caso no ponto A.
Decalagem de acordo com a ABNT/NBR: 6118 (2014)
Conforme visto, uma vez que podemos calcular a área de aço de uma seção com base na seção adjacente mais desfavorável, a norma ABNT/NBR: 6118 (2014) propõe solucionar o problema apenas deslocando o diagrama de momento fletor, processo comumente denominado de decalagem.
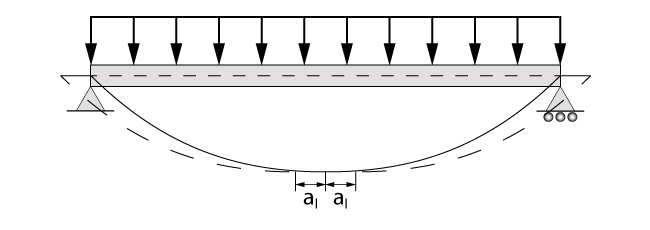
Conforme observado na verificação de cisalhamento de vigas de concreto, a norma brasileira utiliza dois modelos de treliça para representar o comportamento de vigas de concreto.
Decalagem no modelo I
Para o modelo I, as diagonais comprimidas estarão dispostas a 45º e a parcela \mathrm{V_c} terá um valor constante. O valor do deslocamento do diagrama de momentos fletores será fornecido pela equação abaixo.
\mathrm{a_l = d \cdot \left[ \dfrac{V_{Sd,máx}}{2 \cdot (V_{Sd,máx} - V_c)} \cdot (1 + cotg \alpha) - cotg \alpha \right] \leq d}
onde:
\mathrm{a_l = d}, para \mathrm{V_{Sd,máx} \leq V_c}. \mathrm{a_l \geq 0,5 \cdot d}, no caso geral; \mathrm{a_l \geq 0,2 \cdot d}, para estribos em 45º.Considerando agora estribos verticais, que é o mais usual, podemos simplificar um pouco a formulação acima.
\mathrm{a_l = d \cdot \left[ \dfrac{V_{Sd,máx}}{2 \cdot (V_{Sd,máx} - V_c)}\right] \leq d}
Decalagem no modelo II
Já no modelo II, o ângulo de inclinação das bielas \mathrm{\theta}, pode variar de 30º a 45º e a parcela complementar \mathrm{V_c} sofrerá redução com o aumento de \mathrm{V_{Sd}}.
\mathrm{a_l = 0,5 \cdot d \cdot (cotg \theta - cotg \alpha)}
onde:
\mathrm{a_l \geq 0,5 \cdot d}, no caso geral; \mathrm{a_l \geq 0,2 \cdot d}, para estribos em 45º.Considerando também os estribos verticais, teremos a equação abaixo.
\mathrm{a_l = 0,5 \cdot d \cdot cotg \theta}
Exemplo aplicado
A fim de aplicar o conceito de decalagem, vamos analisar uma viga contínua, de 14 cm de largura por 30 cm de altura, com dois vãos de 4,0 m, submetida a um carregamento distribuído de 10 kN/m. Utilizaremos um concreto classe C20 e será considerada uma altura útil de 27,5 cm.
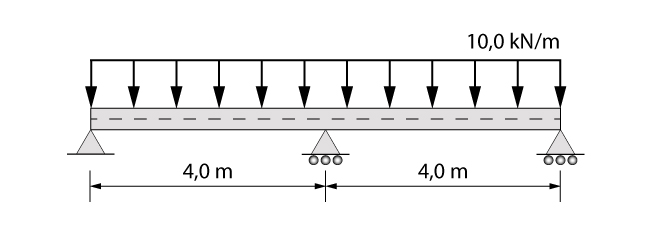
Análise e dimensionamento da viga
Para esse exemplo, iremos analisar apenas o momento negativo localizado na região do apoio central.
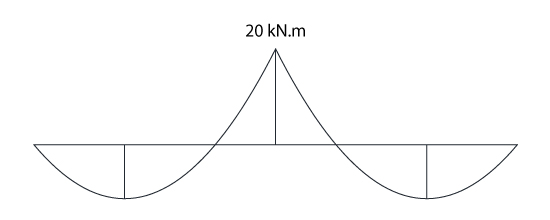
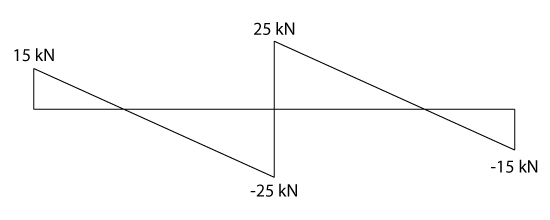
Traçando o diagrama momento fletor e o diagrama esforço cortante da viga obtemos um momento negativo de 20 kN.m e um esforço cortante máximo de 25 kN, conforme ilustram as figuras abaixo. Para a resolução desse exemplo a viga foi analisada com utilização do software Ftool.
Utilizando o momento de cálculo de \mathrm{M_{Sd}=1,4 \cdot 20 = 28 \; kN \cdot m} em nossa calculadora de flexão, obtemos uma área de aço de 2,67 cm², conforme ilustra a figura abaixo.
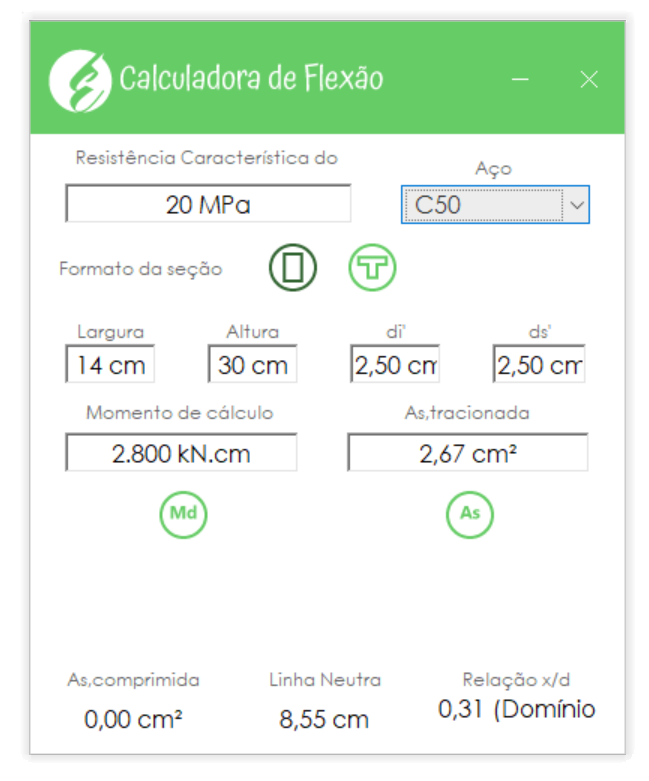
A partir de uma tabela de área de aço por quantidade de barras, utilizaremos 4 barras de 10 mm na seção central, o que resulta em uma área de aço efetiva de 3,2 cm².
Cálculo do valor do deslocamento
Partindo agora para o cálculo de \mathrm{a_l}, temos que decidir o modelo que será utilizado na resolução. Nesse exemplo utilizaremos o modelo I. Vale lembrar que ao utilizarmos o modelo I para o cálculo de \mathrm{a_l}, devemos utilizar o mesmo nas demais verificações, por exemplo: verificações de cisalhamento e verificações de torção.
Inicialmente devemos calcular o valor de \mathrm{V_c}:
\mathrm{V_c = 0,09 \cdot f_{ck} ^{\frac{2}{3}} \cdot b_w \cdot d}
\mathrm{V_c = 0,09 \cdot \dfrac{20 ^{\frac{2}{3}}}{10} \cdot 14 \cdot 27,5 = 25,5 \; kN}
Como \mathrm{V_{Sd,máx} = 1,4 \cdot 25 = 35 > V_c}, vamos prosseguir calculando o valor de \mathrm{a_l}.
\mathrm{a_l = d \cdot \left[ \dfrac{35}{2 \cdot (35 - 25,5)}\right] \leq d}
\mathrm{a_l = 1,84 \cdot d \leq d}
Como o limite de \mathrm{a_l} vale \mathrm{d}, consideraremos \mathrm{a_l = d = 27,5 \; cm}.
Deslocando o diagrama
Agora iremos deslocar o diagrama no valor encontrado de 27,5 cm. Repare que todo o procedimento está sendo realizado graficamente, mas também poderia estar sendo realizado analiticamente a partir das equações do momento fletor.
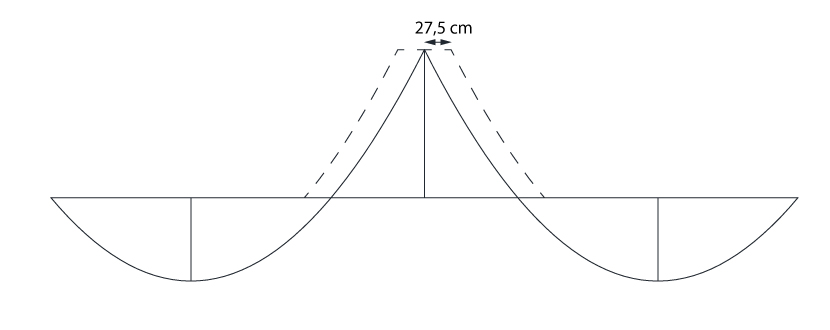
Distribuição de barras de aço
Nesse ponto, já seria possível detalhar as 4 barras de 10 mm cobrindo todo o comprimento em que o diagrama deslocado está negativo. Mas observe que, uma seção deslocada da seção central (seção em que foi obtida o momento máximo e que a área que foi calculada) não requer toda a área de aço calculada (as 4 barras) para essa seção central.
Uma forma de balancear a utilização das armaduras é dividindo o pico do diagrama pelo número de barras. No caso em que encontramos 4 barras de 10 mm, a ordenada do momento fletor será dividida em 4 espaços, conforme ilustra a figura abaixo.
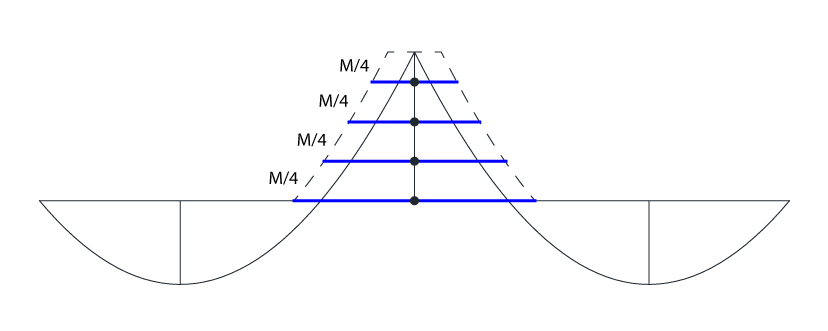
Assim, teremos uma barra para cada comprimento azul ao invés de 4 barras com o comprimento maior. Além do comprimento obtido até aqui ainda devemos acrescentar ainda o comprimento de ancoragem, mas isso é assunto para outro post.
A fim de aliar economia de aço com exequibilidade do serviço, vamos considerar apenas dois grupos de armadura, conforme apresentado na figura abaixo.
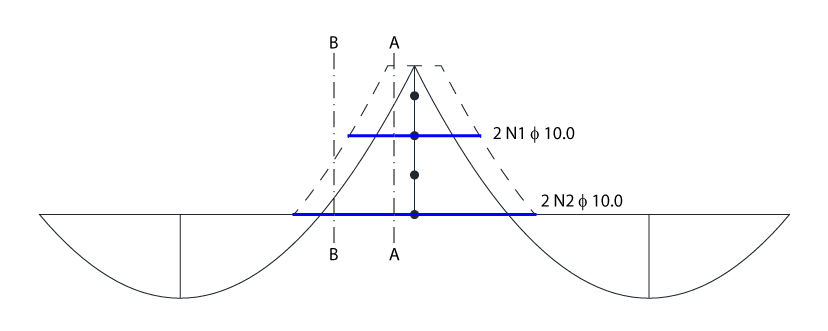
Dessa forma, obteremos os detalhamentos transversais apresentados na figura abaixo, em que o corte A mostra o trecho em que estão presentes apenas duas barras de 10 mm e o corte B mostra o trecho em que encontra-se quatro barras de 10 mm.
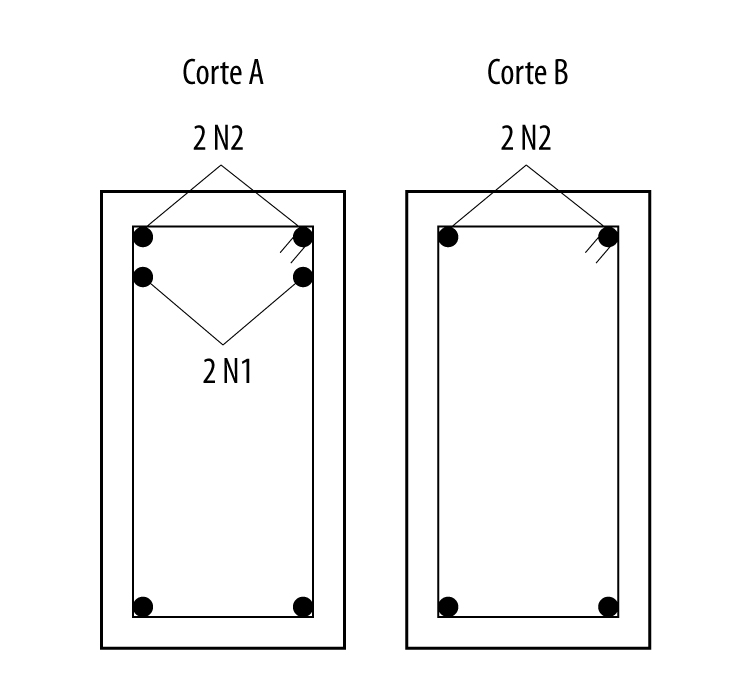
Automatização com softwares
Em softwares de cálculo, devemos ter uma atenção maior com a parte de análise estrutural, uma vez que o dimensionamento e o detalhamento são realizados de forma automática. A figura abaixo ilustra uma decalagem automática do software TQS.
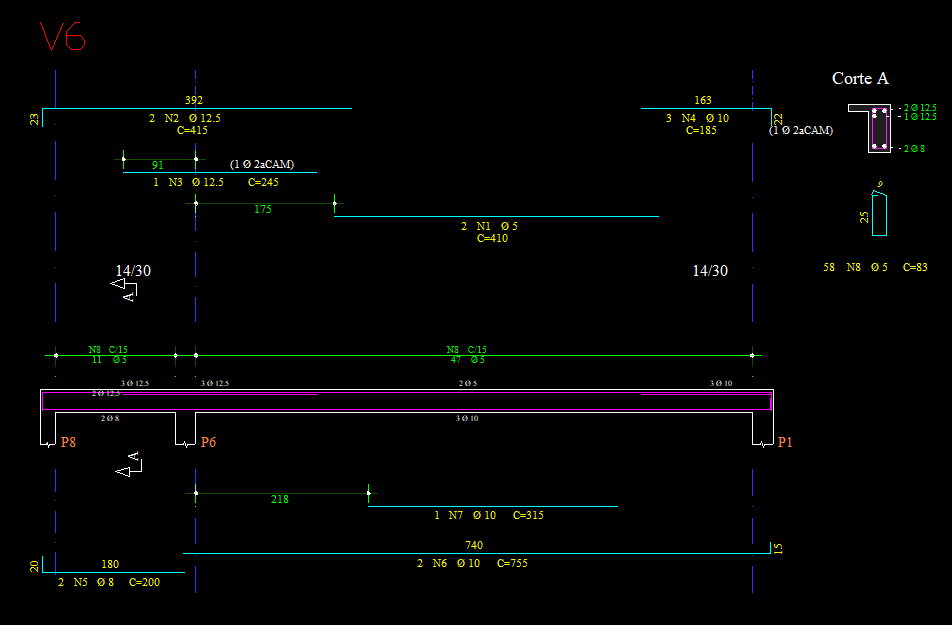
Se você se interessou por esse conteúdo, quero convidar você para conferir o curso Essencial em Concreto Armado do professor Rangel Lage em que você irá aprender a utilizar o software TQS (na minha opinião, o melhor software do mercado) passando por TODAS as etapas (desde a concepção estrutural até elaboração das pranchas) necessárias para o desenvolvimento de um projeto completo.
Recado final
Nesse post você aprendeu o conceito de decalagem e como distribuir as barras realizando economia na obra. Se você gostou desse texto ou se ainda possui alguma dúvida, deixe uma mensagem nos comentários abaixo!
Fonte:
ARAÚJO, J. M. Curso de Concreto Armado. Rio Grande: Editora Dunas, 2014. v. 1
ASSOCIAÇÃO BRASILEIRA DE NORMAS TÉCNICAS. NBR 6118: Projeto de estruturas de concreto – Procedimento. Rio de Janeiro, 2014.
CARVALHO, R. C.; FIGUEIREDO FILHO, J. R. Cálculo e Detalhamento de Estruturas Usuais de Concreto Armado Segundo a NBR 6118:2014. São Carlos: EdUFSCar, 2014.
Gostaria de ter acesso a um curso sobre modelagem de alvenaria estrutural no Revit?
Aproveite enquanto está com um preço especial.

Muito boa explicações! para bens.
Muito obrigado pelo comentário, Albino!
Muito boa a explicação. Obrigado!
Você possui alguma aula que trata do calculo de Vc para viga submetidas a flexo compressão? (Quando Vc = Vc0 (1 + M0/Msd,max) para o modelo I).
Não encontro material sobre esse assunto em lugar algum, nem para figas com flexo compressão quanto para vigas protendidas.
Obrigado e parabéns pelo trabalho!
E ai, Robson,
No momento não tenho nada escrito sobre vigas submetidas a flexo-compressão
Mas no futuro escreverei
Abraços!
Gostei muito das suas explicações e de sei jeito paciencioso de explicar ,meus parabéns
Muito obrigado, Marcos!
José, que objetivo seu post!! E mais ainda o esquema que ilustra os comprimentos de barras no momento negativo. Meus parabéns. Procurei no google o conceito de decalagem na engenharia civil e apareceu esse seu post logo no 3º link após as apostilas de concreto armado do prof Dr. Paulo José Bastos da Unesp Bauru, que é uma leitura bem mais densa para quem quer se aprofundar um pouco. Novamente, obrigado, e parabéns!!
Fico muito feliz que tenha ajudado, João.
Forte abraço!