Dimensionamento de escadas de concreto armado

Você se sentiria confiante se um cliente lhe solicitasse hoje o dimensionamento de uma escada de concreto armado? Pois saiba que o cálculo de escadas são bem similares ao dimensionamento de lajes.

A seguir você aprenderá, passo a passo, como calcular escadas de concreto armadas longitudinalmente, partindo da obtenção das ações até o detalhamento da armação da escada.

Dimensões de escadas

Em primeiro lugar, vamos analisar as dimensões das escadas. Em geral, as mesmas já são fornecidas pelo projeto de arquitetura mas uma regra conhecida como Fórmula de Blondel pode nos ajudar a definir essas dimensões:

\mathrm{60 \leq p + 2 \cdot e \leq 64}

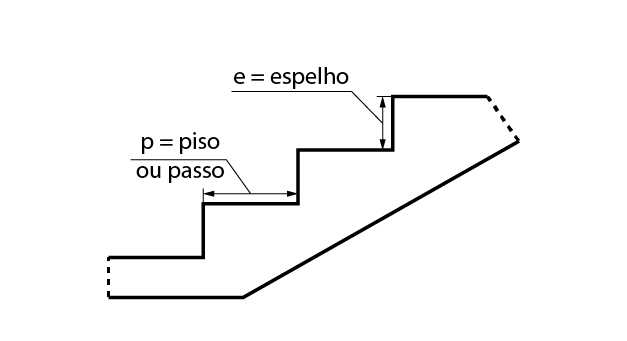
Onde p representa o “piso” ou “passo” e varia normalmente de 25 a 30 cm e o e representa o espelho e varia normalmente de 16 a 18 cm.

Vale lembrar que nosso foco aqui não é não definição das dimensões dos degraus e espelhos de uma escada e sim a obtenção da armação necessária na mesma.

A fim de definirmos a largura do lance, é recomendado a largura mínima de 100 cm, sendo usual o uso de 120 cm como largura.

Ações em escadas

Em segundo lugar, vamos estudar sobre as ações que normalmente atuam em escadas. Essa ações, podem inclusive serem utilizadas em escadas metálicas, desde que sejam feitas as devidas alterações de materiais.

Peso próprio

O peso próprio na região dos patamares pode ser calculado igual fazemos em lajes maciças, apenas multiplicado a espessura pelo peso específico do concreto. Para os trechos inclinados uma solução muito utilizada é calcular o peso próprio a partir de uma espessura média de concreto.

A espessura média pode ser calculada através das equações abaixo:

\mathrm{cos \alpha = \dfrac{p}{\sqrt{e^2 + p^2}}}

\mathrm{h_1 = \dfrac{h}{cos \alpha}}

\mathrm{h_m = h_1 + \dfrac{e}{2}}

Ao reduzir as equações acima obtemos:

\mathrm{h_m = \dfrac{h}{\dfrac{p}{\sqrt{e^2 + p^2}}} + \dfrac{e}{2}}

Revestimento

O revestimento, assim como o peso próprio, é considerado como uma carga vertical por metro quadrado de projeção horizontal. O mesmo vai variar do material que o arquiteto detalhou em seu projeto. Na ausência dessa informação é recomendado utilizar uma carga de revestimento de 1,0 kN/m².

Parapeito

Uma outra ação que deve ser analisada ao calcularmos uma escada é a originada pelo peso dos parapeitos. Muitas vezes os mesmos são apoiados diretamente sobre vigas laterais, sendo assim, o carregamento não é considerado no dimensionamento da escada.

Utilizando a altura, espessura e peso específico do material que compõe o parapeito é possível calcular a carga distribuída por metro:

\mathrm{\gamma_a \cdot H \cdot t, \; kN/m}

Apenas para exemplo, podemos calcular a carga de um parapeito de tijolo cerâmico furado (\mathrm{\gamma_a = 13 \; kN/m^3}) com 15 cm de espessura e 1,0 m de altura:

\mathrm{\gamma_a \cdot H \cdot t = 13 \cdot 1,0 \cdot 0,15 =1,95 \; kN/m}

Sobrecarga de utilização

Usualmente, a única ação variável presente em escadas são as sobrecargas de utilização, também conhecidas como carga acidentais, que de acordo com a norma atualizada ABNT/NBR: 6120 (2019) devemos considerar:

• 3,0 kN/m² para escadas em residências e hotéis, no caso de uso comum, ou em edifícios comerciais, clubes, escritórios e bibliotecas
• 2,5 kN/m² para escadas em residências e hotéis (dentro de unidades autônomas)

Ao existirem parapeitos apoiados sobre a escada, a norma ABNT/NBR: 6120 (2019) informa que deve-se considerar uma ação horizontal \mathrm{p} kN/m aplicada a uma altura de 1,1 m, independente da altura do parapeito.

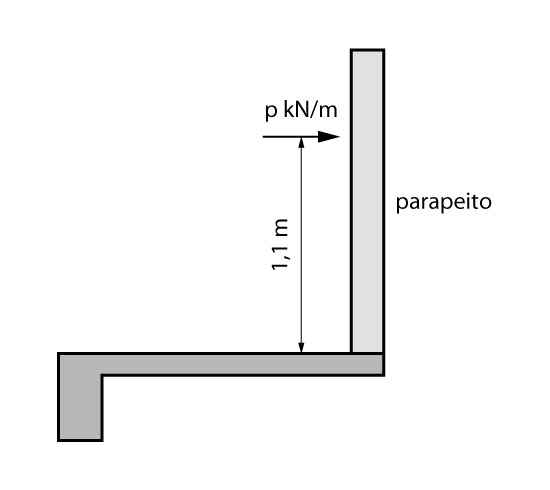
Segue abaixo o valor de \mathrm{p} para situações mais usuais:

• 1,0 kN/m para áreas privativas de unidades residenciais, escritórios, quartos de hotéis,
  quartos e enfermarias de hospitais, coberturas, terraços, passarelas etc. sem acesso público
• 1,0 kN/m para escadas privativas ou sem acesso público, escadas de emergência em edifícios
• 2,0 kN/m para escada panorâmicas

Modelo de cálculo

Nesse post, trataremos apenas do caso em que a escada trabalha em sua direção longitudinal.

Para o modelo estrutural de uma escada apoiada no nível inferior, no nível superior e no nível intermediário (viga do patamar), um modelo composto apenas por elementos de barra é o suficiente para a obtenção dos esforços.

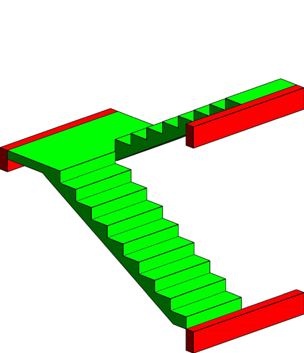
A figura abaixo ilustra um modelo estrutural de um lance de uma escada:

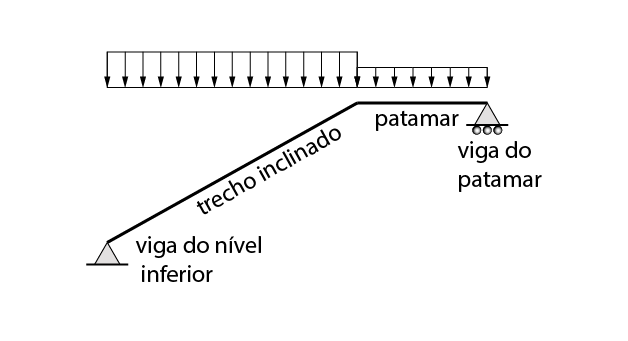
Exemplo aplicado

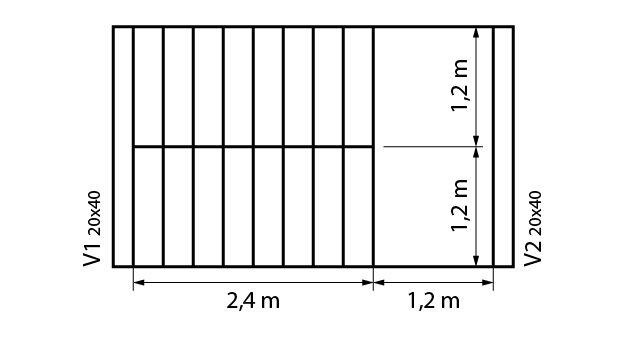
A fim de aplicarmos os conceitos acima estudados, vamos calcular uma escada com lances adjacentes com espelho de 17 cm, piso (ou passo) de 30 cm e espessura de 12 cm.

Essa escada será executada com concreto C20 e a mesma é apoiada sobre vigas nos níveis inferiores e superiores, assim como no nível do patamar, por vigas de 20 cm de largura.

O pé direito do pavimento é de 3,06 m e o patamar está localizado a meia altura (1,53 m).

Caso você prefira, pode acompanhar essa resolução através de um vídeo no nosso canal do YouTube:

Calculo das ações

Para esse exemplo temos que calcular 4 ações: peso próprio na região do patamar, peso próprio na região inclinada, revestimento e carga acidental distribuída uniformemente.

O peso próprio do patamar pode ser calculado apenas multiplicando a espessura pelo peso específico do concreto:

\mathrm{g_{pat} = 0,12 \cdot 25 = 3 \; kN/m^2}

Para o peso próprio da região inclinada é necessário calcular inicialmente uma espessura média, que pode ser calculada pela equação simplificada abaixo:

\mathrm{h_m = \dfrac{h}{\dfrac{p}{\sqrt{e^2 + p^2}}} + \dfrac{e}{2}}

\mathrm{h_m = \dfrac{0,12}{\dfrac{0,30}{\sqrt{(0,17)^2 + (0,3)^2}}} + \dfrac{0,17}{2}}

\mathrm{h_m = 0,22293 \; m}

\mathrm{g_{inclinado} = 0,22293 \cdot 25 = 5,57 \; kN/m^2}

A escada será considerada sem acesso ao público, logo a sobrecarga de utilização é de 2,5 kN/m². Para o revestimento iremos considerar o valor de 1,0 kN/m².

Em resumo, no trecho do patamar temos um carregamento total de 6,5  kN/m² (somatório de revestimento, carregamento acidental e peso próprio na região do patamar) e no trecho inclinado de 9,07 kN/m² (somatório de revestimento, carregamento acidental e peso próprio na região do patamar).

Obtenção dos esforços

A partir das ações calculadas acima é possível calcular os esforços solicitantes utilizando apenas um modelo composto por elementos de barra.

Como temos carregamentos distribuídos por área (kN/m²), é necessário multiplicarmos por uma largura para obtermos carregamentos distribuídos linearmente (kN/m) e resolvermos o modelo.

Assim sendo, utilizaremos uma faixa de 1,0 m de largura. Ou seja, apenas como exemplo, um carregamento de 9,07 kN/m² será uma carga distribuída linearmente de 9,07 kN/m em uma faixa de 1,0 m de largura.

O modelo utilizado para obtenção dos esforços pode ser observado na figura abaixo:

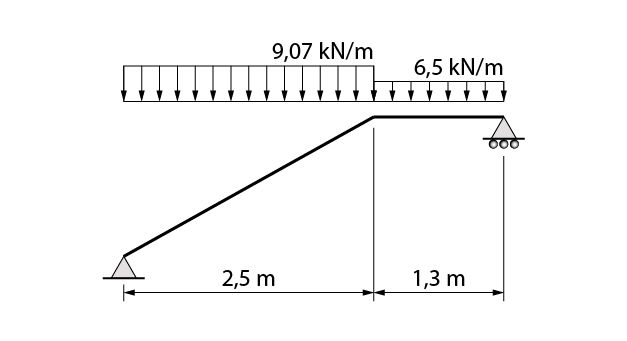
Observe que a projeção horizontal do trecho inclinada e a dimensão do trecho reto foram incrementadas em 10 cm, uma vez que o apoio foi considerado no eixo das vigas.

Você já pensou em detalhar escadas plissadas de concreto armado de uma forma bem simplificada? Dá uma conferida no vídeo abaixo:

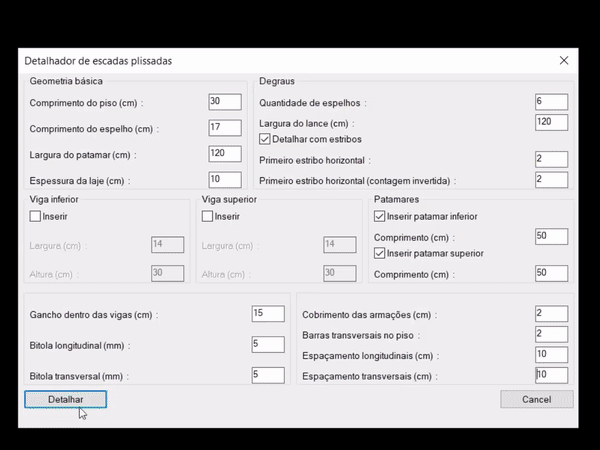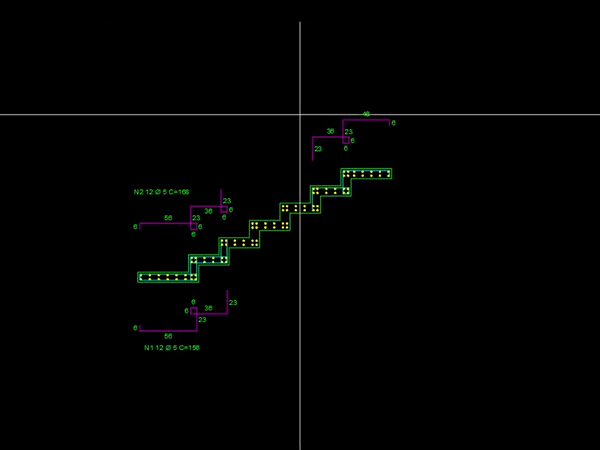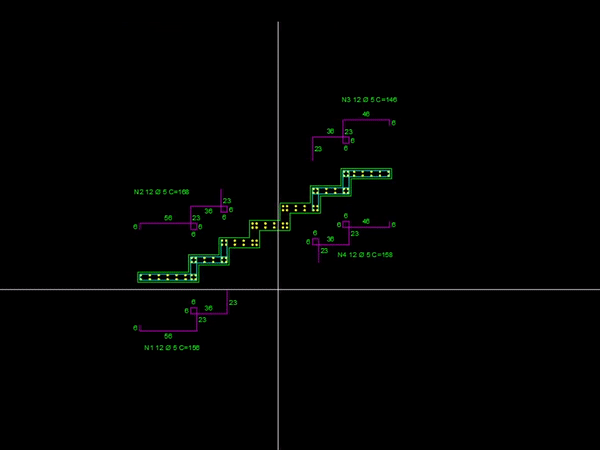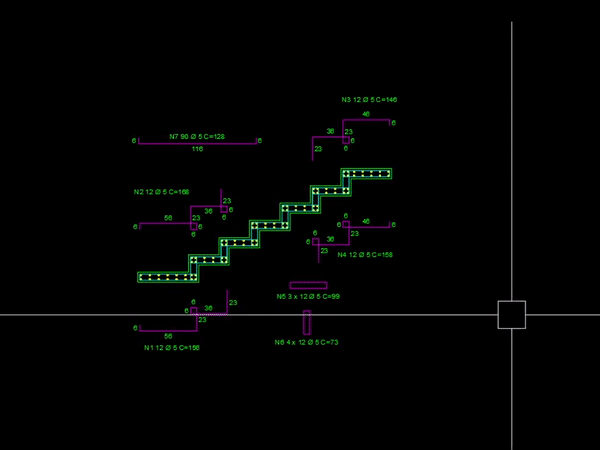
Pois é, essa é uma rotina de detalhamento de escadas plissadas que foi desenvolvida para o AutoCAD. Caso queira conferir mais sobre essa ferramenta basta acessar o link anterior.

É possível obter a reação do apoio esquerdo pela equação abaixo:

\mathrm{V_A=\dfrac{9,07 \cdot 2,5 \cdot (1,25+1,3)}{3,8}+\cdots}

\mathrm{\dfrac{6,5 \cdot 1,3 \cdot 0,65}{3,8}=16,66 \; kN}

Com isso a equação de momento fletor do primeiro trecho fica:

\mathrm{M(x)=16,66 \cdot x - 9,07 \cdot \dfrac{x^2}{2}}

Aplicando x igual a 2,5 m obtemos o valor 13,3 kN.m. A fim de calcular o máximo momento fletor no trecho um podemos derivar a equação acima e igualar a zero:

\mathrm{-9,07 \cdot x +16,66 = 0 \rightarrow x = 1,837}

Aplicando x igual a 1,837 m obtemos o momento fletor de 15,3 kN.m, que é o momento fletor máximo atuante no lance.

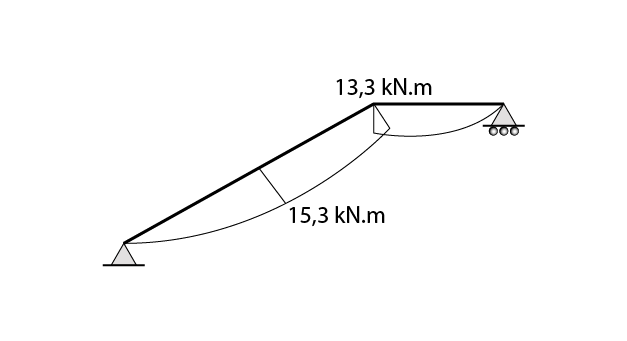
Os esforços acima também poderiam ser obtidos em softwares de análise de estruturas, como por exemplo o software gratuito Ftool.

Dimensionamento da escada

Considerando a altura útil igual a 9,5 cm, para resistir a um momento de 15,3 kN.m (momento fletor máximo) será necessário uma área de aço de 5,83 cm²/m. O processo de obtenção dessa área de aço é basicamente o mesmo realizado no dimensionamento de vigas de concreto armado, e por isso não será detalhado nessa publicação.

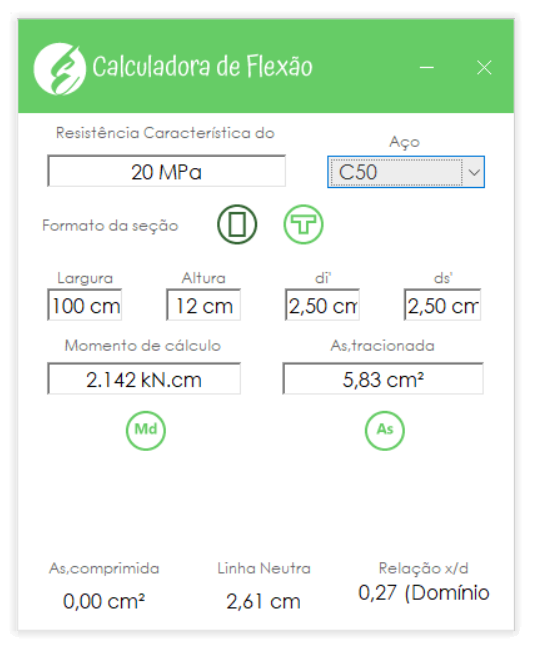
Como esperando, obtivemos os mesmos \mathrm{As = 5,83 \; cm^2} utilizando a calculadora.

[formulario-calculadora-flexao]

Detalhamento da escada

Usando a tabela a abaixo para converter uma área de aço por metro em uma bitola e um espaçamento chegamos em barras de 10 mm a cada 12,5 cm (6,4 cm²/m efetivos).

Finalmente, como a largura de cada lance é 1,2 m utilizaremos 10 barras de 10 mm para o detalhamento do lance.

É importante perceber que nesse post não fizemos nenhuma verificação de estado limite de serviço: verificação dos deslocamentos (conforme visto nas verificações de deslocamento de lajes nervuradas) e de fissuração.

Apesar de usualmente escadas não necessitarem de armadura para resistir esforço cortante, essa verificação ainda deve ser feita. Podemos utilizar a mesma verificação realizada para cisalhamento em lajes.