Distribuição de tensões nos solos: tensões geostáticas

Nós sabemos que para o adequado dimensionamento de uma obra geotécnica, seja ela fundação ou contenção, é imprescindível o correto cálculo das tensões atuantes e resistentes do solo.

As tensões admissíveis podem ser determinadas de forma simplificada através de correlações com o resultado do ensaio de SPT.

Já as tensões atuantes são resultado dos esforços que solicitam um maciço de solo.

Nesse post veremos um pouco sobre alguns tipos de tensões atuantes no solo, dando uma maior ênfase, inicialmente, no cálculo das tensões geostáticas.

Distribuição de tensões no solo

As tensões no solo, de maneira simplificada, podem ser divididas em geostáticas e induzidas.

As tensões geostáticas são aquelas decorrentes do próprio peso próprio do solo e da água presente em seus interstícios.

Já as tensões induzidas são causadas por elementos externos, podendo ser sobrecarga de trânsito, fundações, etc.

De maneira geral, as tensões geostáticas serão mais elevadas quanto maior for a profundidade do ponto analisado, enquanto as tensões induzidas serão menores quanto maior a distância do ponto analisado ao ponto de aplicação na carga, como podemos ver na figura abaixo.

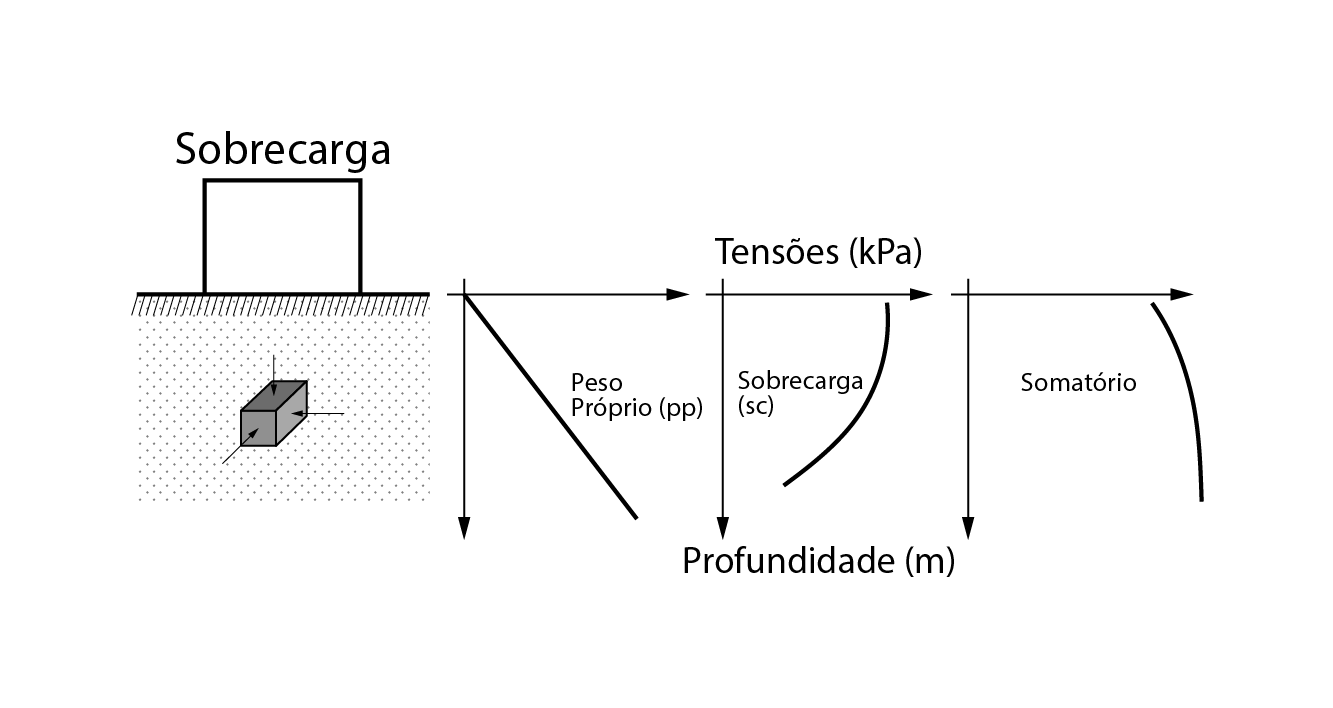
As tensões em um ponto no interior do maciço de solo se desenvolvem no espaço, ou seja, em três dimensões, porém, podemos simplificar o problema, adotando-o como um plano, logo consideraremos as tensões atuantes apenas em dois eixos ortogonais entre si.

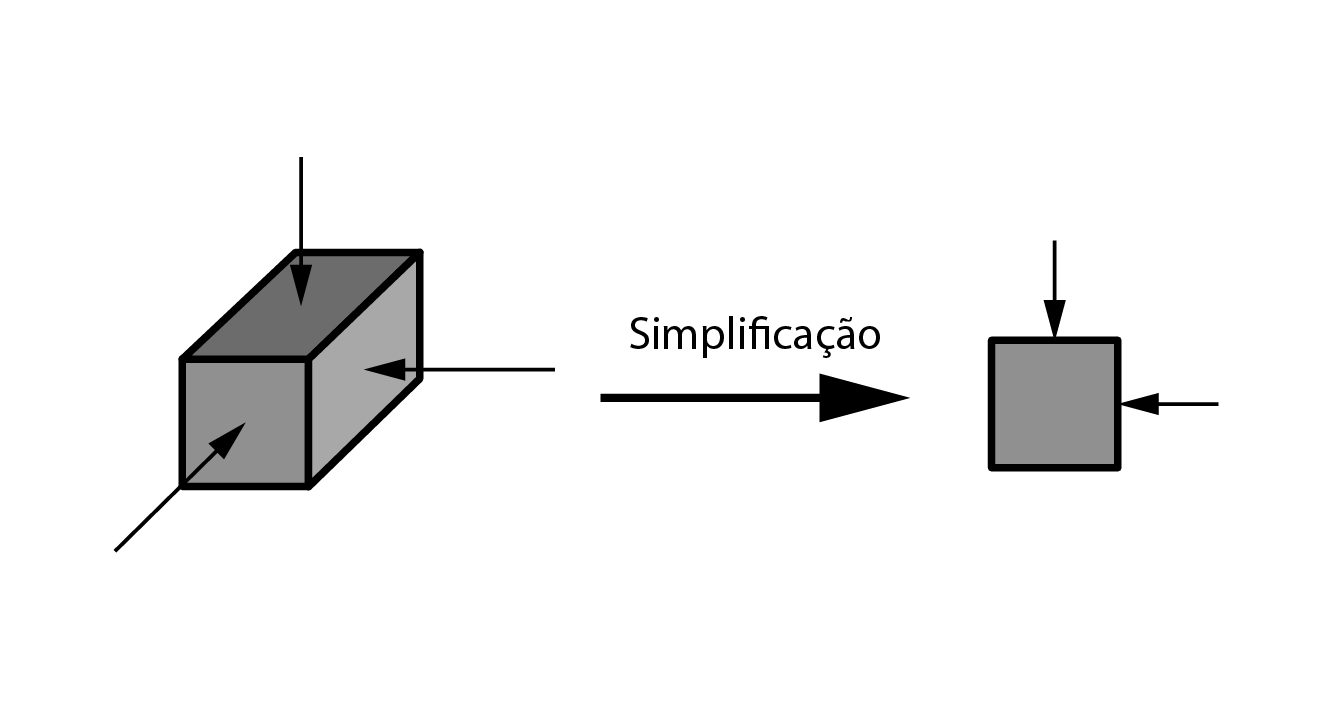
Ainda com tal simplificação, o correto cálculo das tensões atuantes decorrentes do peso próprio do maciço e de sobrecargas é um problema complexo, pois dependem de muitas variáveis.

A seguir iremos ver o cálculo das tensões geostáticas para várias situações específicas, a fim de tentar facilitar o entendimento do conteúdo.

Tensões Geostáticas

Como dito anteriormente, o cálculo do estado de tensões ocasionadas pelo peso próprio do maciço pode ser bastante complexo principalmente pela irregularidade de topografia ou heterogeneidade do material.

Entretanto, em alguns casos, a distribuição de tensões pelo peso próprio é simplificada. Tal caso é chamado de geostático e é caracterizado por:

• Superfície horizontal do terreno;
• Baixa variação das propriedades do solo ao longo da profundidade;
• Caso existam subcamadas de solo, as mesmas também são horizontais;
• Se houver água no solo, a mesma encontra-se em condição estática;

Tal idealização pode ser correlacionada com a análise do processo de deposição de um solo sedimentar, onde a deposição de camadas acarreta um acréscimo de tensões e geram deformações no solo, porém, sem deslocamentos horizontais, visto que há uma compensação na tendência de deslocamentos entre elementos adjacentes.

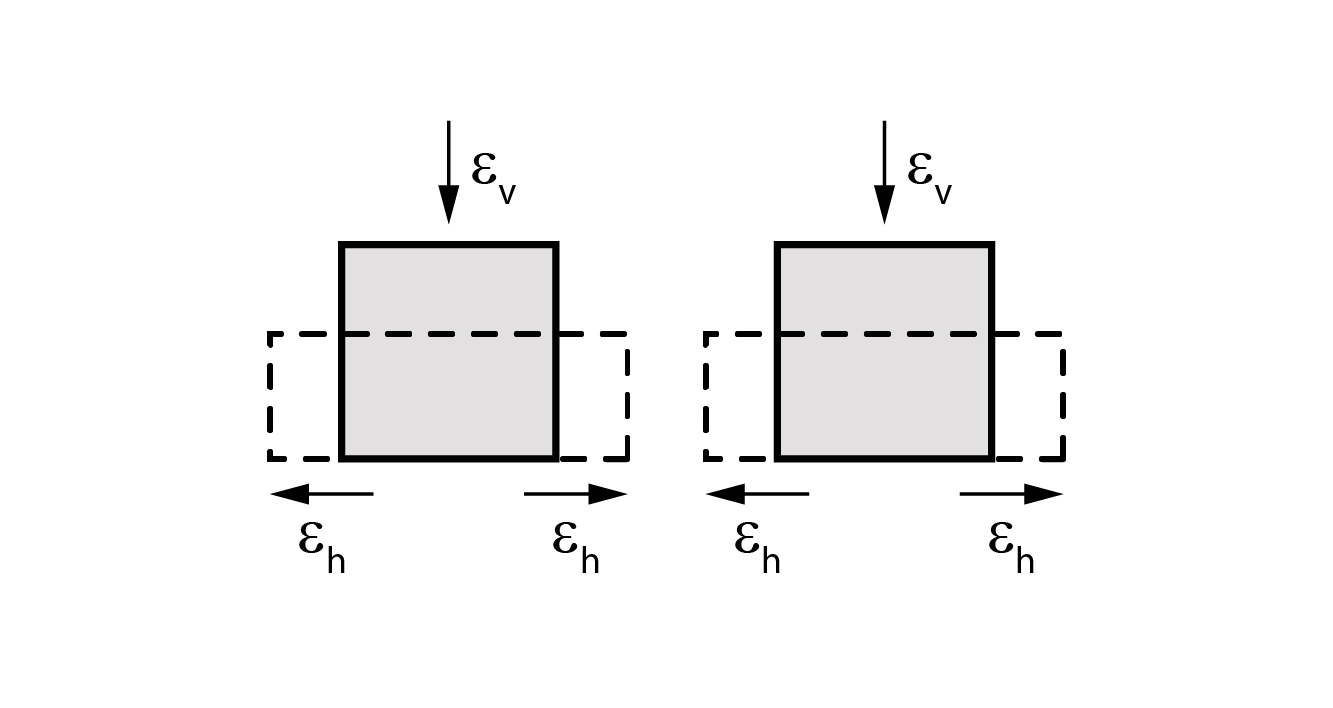
Tensão geostática vertical

A tensão vertical, em qualquer profundidade, é calculada simplesmente considerando o peso de solo acima daquela profundidade.

Logo, se o peso específico do solo é constante em cada uma das camadas, a tensão vertical total pode ser calculada a partir da seguinte formulação:

\mathrm{\sigma_v = \gamma \cdot z}

Onde:

• \mathrm{\sigma_v} : tensão vertical total em um determinado ponto do solo;
• \mathrm{\gamma} : peso específico do solo;
• z: profundidade do ponto analisado.

No caso em que há estratificação do terreno, ou seja, existam mais de uma camada de solo, deve ser calculado de maneira similar, porém levando em conta o peso de todas as camadas de solo, seguindo a seguinte formulação:

\mathrm{\sigma_v = \sum \gamma_i \cdot z_i}

Para melhor entendimento da formulação, segue a imagem de um exemplo simples de solo estratificado.

Outro caso possível é a presença do nível d’água no solo.

Nesse caso, os vazios do solo são preenchidos por água. Para uma situação em que não há fluxo de água no interior do solo, ou seja, a água encontra-se em condição estática, o cálculo da pressão suportada pela água é feito simplesmente considerando o peso da coluna de água acima do ponto analisado:

\mathrm{u = \gamma_w \cdot h_w}

Onde:

• u: pressão resistida pela coluna d’água (poropressão);
• \mathrm{\gamma_w}: peso específico da água;
• \mathrm{h_w}: altura da coluna d’água.

Há ainda tensões horizontais atuantes, que são relacionadas com as tensões verticais, mas tal conteúdo é tratado com mais ênfase no post sobre empuxos do solo.

Tensões totais, efetivas e poropressão

Como já discutido, os solos são sistemas multifásicos, em que as partículas sólidas são distribuídas de maneira aleatória e apresentam espaços vazios entre elas, sendo estes contínuos e ocupados por ar e/ou água.

Então, é preciso entender a natureza da distribuição de tensões ao longo de determinada seção, considerando tal heterogeneidade do material analisado.

A tensão total, como falamos anteriormente, pode ser dividida em duas partes:

1. Parcela suportada pela água nos espaços vazios. A tal tensão daremos o nome de poropressão (ou pressão neutra);
2. Restante da tensão total suportado pelos sólidos em seus pontos de contato. A soma das componentes verticais das forças desenvolvidas em tais pontos por unidade de área de seção transversal é chamada de tensão efetiva.

Então, a tensão total vertical no solo pode ser escrita como:

\mathrm{\sigma_v = \sigma^{'} + u}

Onde:

• \mathrm{\sigma^{'}}: tensão efetiva;
• u:  poropressão;

Tal conhecimento, de que apenas uma parcela da tensão total é transmitida aos grãos, possibilita um melhor entendimento do comportamento de solos saturados, principalmente a características como resistência e compressibilidade.

Propriedades relacionadas às tensões

A compressibilidade do solo é consequência direta do deslocamento relativo entre as partículas do mesmo, conforme figura abaixo.

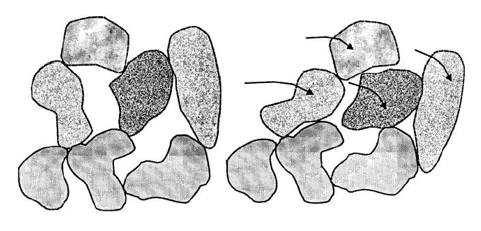
O deslocamento das partículas depende das tensões transmitidas entre os grãos, ou seja, da tensão. Logo, sempre que houver uma variação na tensão efetiva ocorrerão variações volumétricas no solo, podendo ser recalque ou expansão.

Tal variação pode ser gerada por um acréscimo de tensões totais devido a carregamentos externos ou mesmo por variações na poropressão, como no caso de elevação ou rebaixamento de lençol freático.

Outra característica do solo que é intimamente ligada à tensão efetiva é a sua resistência. Uma maior tensão efetiva, ou seja, uma maior tensão normal entre as partículas, eleva a capacidade resistente a cisalhamento do solo.

Vale ressaltar também, que para o cálculo da tensão efetiva em solos que se encontram em camadas submersas é necessário utilizar o peso do solo submerso, de forma que um acréscimo na pressão neutra sobre uma camada não tenha efeito nas propriedades mecânicas do solo.

Exemplo

Vamos calcular a tensão total, efetiva e poropressão no ponto A, de acordo com o perfil de solo ilustrado na figura abaixo.

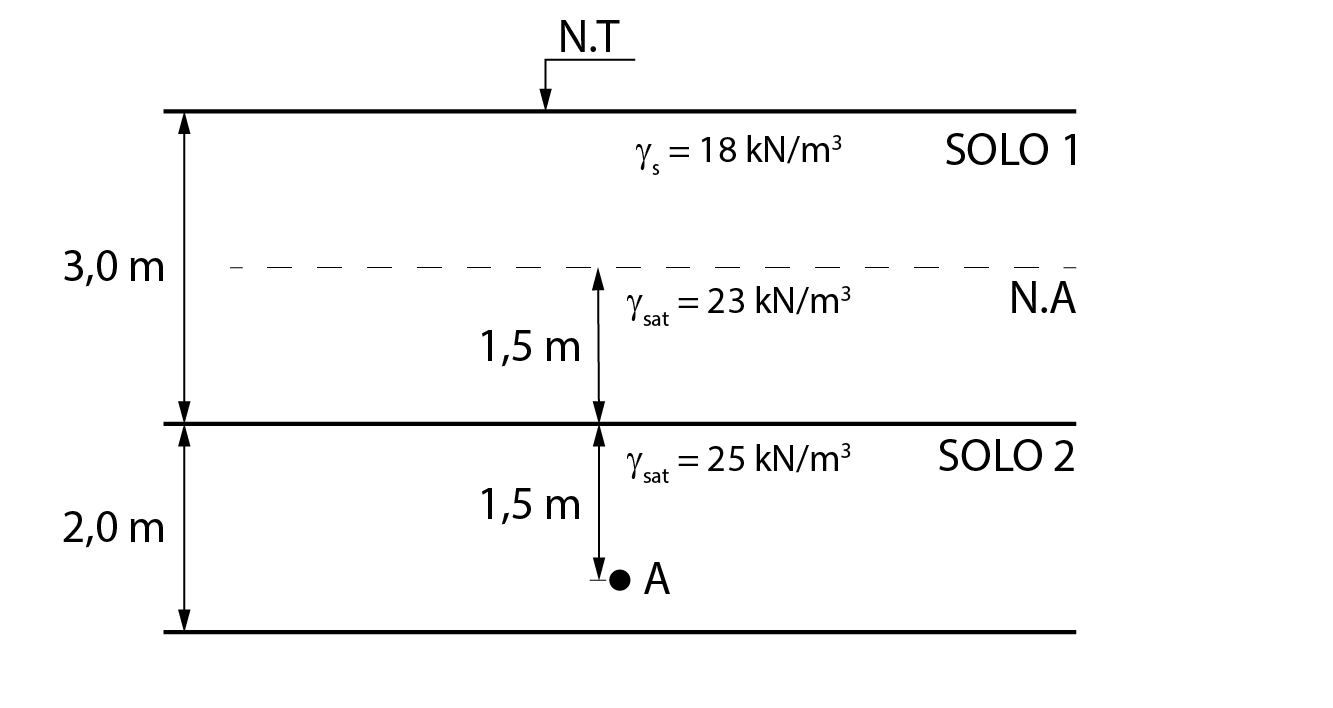
Inicialmente, calcularemos a tensão efetiva no ponto A. Ela será composta pelas seguintes parcelas:

1. Solo 1 seco, que se encontra acima da nível d’água;
2. Solo 1 submerso.
3. Solos 2, que também se encontra submerso.

Logo, temos:

\mathrm{\sigma^{'} = \gamma_{s}^{1} + \gamma_{sub}^{1} + \gamma_{sub}^{2}}

Lembrando que:

\mathrm{\gamma_{sub} = \gamma_{sat} - \gamma_{w}}

E considerando \mathrm{\gamma_{w} = 10 kN/m^{3}}, temos:

\mathrm{\sigma^{'} = 18.0\cdot 1.5 + 13.0\cdot 1.5+ 15.0\cdot 1.5}

\mathrm{\sigma^{'} = 69.0 kN/m^{2}}

Agora, iremos calcular a poropressão. Lembrando que a mesma independe do solo, devemos considerar apenas a altura da coluna d’água acima do ponto A. Logo:

\mathrm{u = \gamma_{w} \cdot h_w = 10.0 \cdot 3.0}

\mathrm{u = 30.0 kN/m^{2}}

Por fim, a tensão vertical total no ponto A será a soma da tensão efetiva com a poropressão. Logo:

\mathrm{\sigma_{v} = 99.0 kN/m^{2}}

Nesse post discutimos um pouco sobre os tipos de tensões às quais os solos podem estar submetidos. Aprendemos sobre os conceitos de tensões geostáticas e como calculá-las.

Se você ainda quer saber mais sobre tensões nos solos, confere nosso post sobre tensões induzidas!

E não deixe de continuar seguindo nosso blog e de nos acompanhar também no YouTube.

Até a próxima, pessoal! =)

---

Fonte:

GERSCOVICH, D. M. S. Tensões em solos. Notas de aula. Rio de Janeiro, 2008.

CAPUTO, Homero Pinto. Mecânica dos solos e suas aplicações. Volume 1. 7ª edição. Rio de Janeiro, LTC, 2015.

DAS, Braja M. Fundamentos de engenharia geotécnica. São Paulo, Thomson Learning, 2007.