Empuxos de terra: conceitos iniciais

Se você já leu nosso post sobre muro de arrimos, percebeu no conceito apresentado que tais muros são responsáveis por suportar as tensões horizontais do solo.

Mas afinal, como surgem essas tensões horizontais e como podemos calculá-las?

Calma!

Isso não é nenhum bicho de sete cabeças.

Depois de ler esse post você não terá mais dúvidas em saber identificar os tipos de tensões horizontais de solo, ou empuxos de terra, e com calculá-los.

Vamos começar?

Empuxos de terra

Bem, antes de aprendermos como devemos calcular os empuxos de terra, devemos entender qual seu significado!

Então, entenda como empuxos de terra as ações ou resultantes das ações horizontais em um maciço de solo e são muito importantes, principalmente, para o dimensionamento de estruturas de contenção.

Então você se pergunta: como se originam tais tensões horizontais nos solos?

Nós já vimos em posts anteriores vários conceitos sobre as tensões verticais nos solos, sejam elas geostáticas, induzidas ou, até mesmo sua aplicação, nos bulbos de tensão.

Pois bem, para entendermos bem como se originam as tensões horizontais no solo, precisamos utilizar dos nossos conhecimentos da Teoria da Elasticidade.

Então, vamos analisar um ensaio de compressão em um corpo de prova.

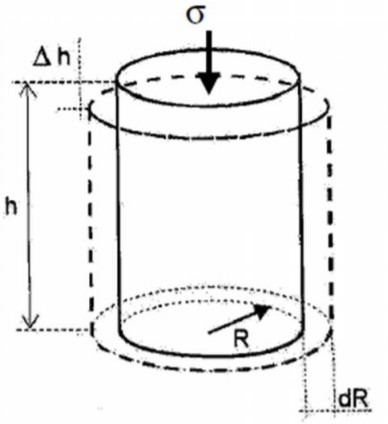
Da Teoria da Elasticidade, temos:

\mathrm{{\varepsilon _v} = \dfrac{{\Delta L}}{L}}

\mathrm{{\varepsilon _h} = \dfrac{{\Delta R}}{R}}

\mathrm{\sigma = \varepsilon \cdot E}

\mathrm{\mu = \dfrac{{{\varepsilon _h}}}{{{\varepsilon _v}}}}

Onde:

• \mathrm{\varepsilon _v}: deformação vertical;
• \mathrm{\varepsilon _h}: deformação horizontal;
• \mathrm{\sigma}: tensão;
• E: módulo de deformabilidade do solo;
• \mathrm{\mu}: coeficiente de Poisson.

Logo, podemos concluir que:

\mathrm{{\varepsilon _h} = \mu \cdot {\varepsilon _v} = \mu \cdot \frac{{{\sigma _v}}}{E}}

Então, o que podemos concluir a partir disso?

Simples! Percebemos através da relação entre as constantes de elasticidade do material (\mathrm{\mu} e E) que existe uma proporcionalidade entre a tensão vertical no solo e sua respectiva tensão horizontal.

Logo, a partir desse momento você sabe que os valores de tensões horizontais podem ser calculados através da tensão vertical efetiva no solo para o mesmo ponto:

\mathrm{{\sigma _h} = k \cdot {\sigma^{'}}_v}

Onde:

• k: coeficiente de empuxo do solo.

Agora que você já entendeu a proporcionalidade entre as tensões e sabe uma fórmula geral para a determinação da tensão horizontal no solo, vamos falar um pouco mais sobre os tipos de empuxo.

Tipologias de empuxo

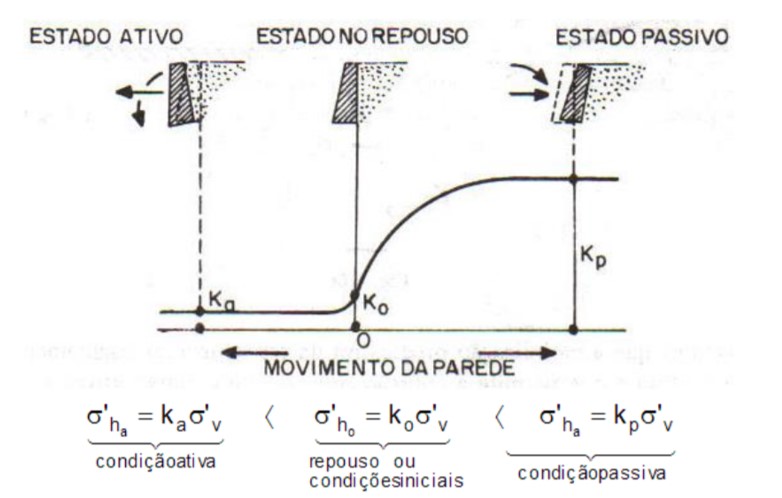
Para falarmos sobre os três tipos de empuxo, vamos imaginar um paramento, ou um plano de contenção, ao longo da altura de um maciço de solo.

Então, poderemos ter três situações distintas para esse paramento: o mesmo encontra-se imóvel, se movimenta em direção ao maciço ou se movimenta na direção oposta ao maciço.

A partir disso, podemos definir os três tipos de empuxo:

• Empuxo no repouso: a massa de solo se mantém em equilíbrio perfeito, sem deformações em sua estrutura, geralmente equilibrada lateralmente pela continuidade do maciço em todas as direções;
• Empuxo ativo: quando o paramento se “afasta” do solo. Nesse caso o solo sofre uma distensão por esse afastamento do plano de contenção, mobilizando sua resistência interna de cisalhamento.
• Empuxo passivo: o solo sofre compressão pela aproximação do plano de contenção. Nesse caso, são mobilizadas tensões de cisalhamento para resistir a essa compressão.

É interessante que você perceba que tanto no empuxo ativo quanto no passivo há a mobilização de tensões de cisalhamento, porém no estado ativo tais tensões reduzem a ação no solo na contenção, enquanto no estado passivo as tensões de cisalhamento aumentam a reação do solo na contenção.

Agora vamos aprender como calculamos tais empuxos!

Empuxo no repouso

O valor do coeficiente do empuxo no repouso (k₀) pode ser obtido de maneira teórica, através dos conceitos de elasticidade, através de experimentos e ensaios laboratoriais ou até mesmo de correlações empíricas.

De maneira geral, baseado em diversos ensaios já realizados e de simplificações admitidas, apresentam-se na literatura diversas tabelas com valores aproximados de coeficientes do empuxo no repouso para diferentes tipos de solo.

Abaixo, apresento uma tabela sugerida por Caputo e Caputo.

Solo	K0
Areia solta	0,45 a 0,50
Areia compacta	0,40 a 0,45
Argila	0,70 a 0,75

Lembrando que essa é apenas uma tabela sugerida, assim como existem diversas outras na literatura. O mais indicado, caso houver condições, é a realização de ensaios com o solo presento no local para determinar seu coeficiente de empuxo no repouso.

Empuxo ativo

Como comentamos anteriormente, empuxo ativo é aquele que ocorre quando o plano de contenção se afasta do maciço de solo, mobilizando tensões cisalhantes que irão diminuir a ação desse solo no paramento.

Para a determinação do coeficiente de empuxo ativo, iremos utilizar a teoria de Rankine.

Rankine, no desenvolvimento de sua teoria faz algumas limitações de forma a simplificar seu modelo e facilitar sua análise. As considerações propostas por Rankine para a determinação dos coeficientes de empuxo do solo são:

• O maciço de solo deve ser considerado plano, horizontal e sem coesão (areia pura seca);
• O solo é formado por uma camada única e contínua (homogêneo);
• É desconsiderado o atrito entre o solo e o paramento no plano de contenção;
• O solo não é submetido a nenhum tipo de sobrecarga de utilização.

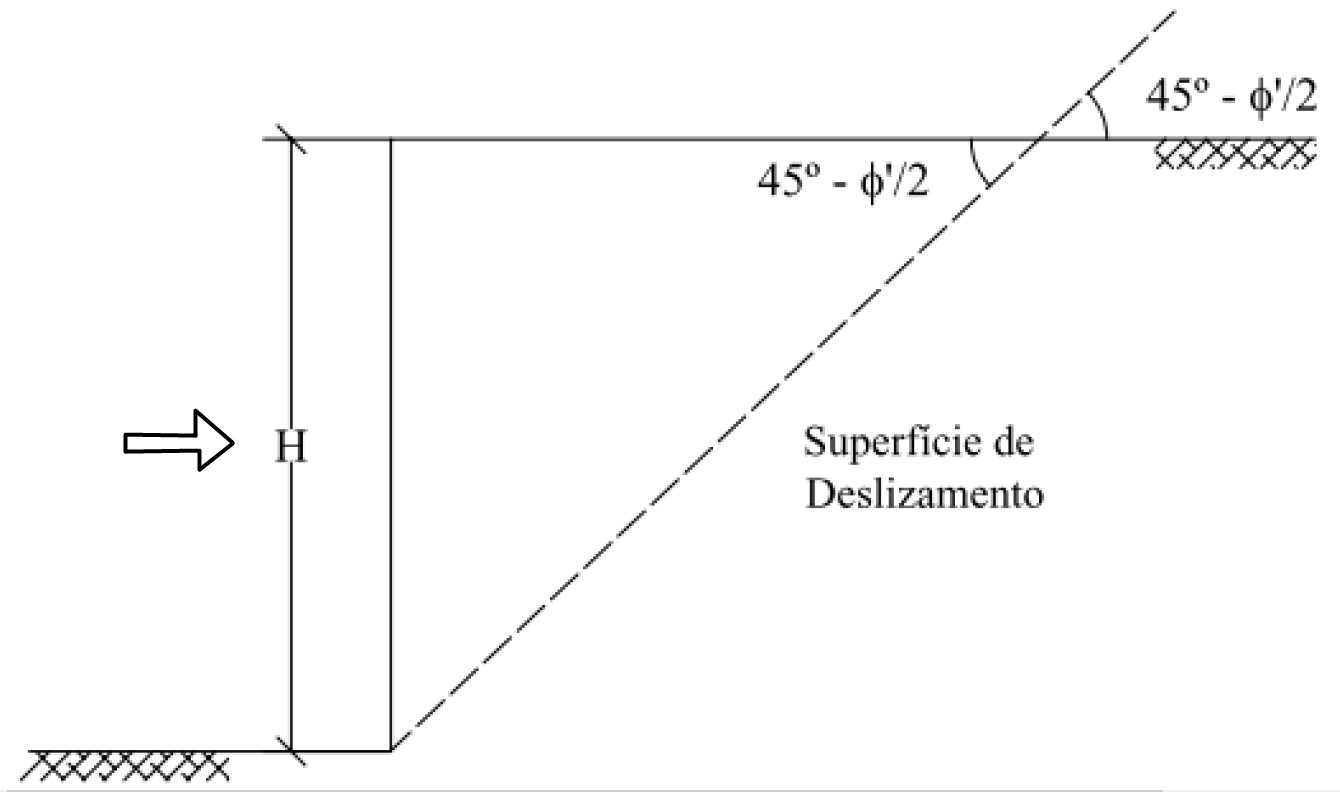
Rankine então, fazendo a análise matemática das forças atuantes em uma cunha de solo instável, com deslocamento no paramento, como ilustrado na figura abaixo, chegou a seguinte formulação:

\mathrm{{k_a} = {\tan ^2}(45 - \varphi /2)}

Onde:

• k_a: coeficiente de empuxo ativo;
• \mathrm{\varphi}: ângulo de atrito interno do solo.

Empuxo passivo

Assim como o coeficiente de empuxo ativo, a determinação do coeficiente de empuxo passivo também pode ser feito a partir da Teoria de Rankine.

Como já falamos, no caso do empuxo passivo, a contenção se move comprimindo o maciço de solo.

Nesse caso, a resistência a cisalhamento é mobilizada e atua aumentando a reação do solo no paramento.

A teoria de Rankine segue as mesmas proposições já citadas e também é feita a partir da análise de uma cunha de solo instável.

A análise nas tensões em tal cunha, leva a seguinte formulação para o coeficiente de empuxo passivo:

\mathrm{{k_p} = {\tan ^2}(45 + \varphi /2)}

Onde:

• k_p: coeficiente de empuxo passivo;

Relação entre empuxo ativo e passivo

Como podemos perceber matematicamente, os coeficientes de empuxo, tanto ativo, como passivo, de acordo com a teoria de Rankine, variam unicamente com o seu ângulo de atrito interno.

Fazendo uma relação matemática simples entre os dois tipos de empuxo, podemos chegar à seguinte formulação:

\mathrm{{k_a} = \dfrac{1}{{{k_p}}}}

Outro fato que podemos perceber pelas formulações, e que já era esperado pela teoria apresentada anteriormente, é que os empuxos ativos tendem a ter valores menores do que os empuxos passivos.

Substituindo alguns ângulos de atrito interno nas equações propostas por Rankine, podemos chegar à seguinte tabela para os valores dos coeficientes de empuxo.

\mathrm{\varphi}	ka	Kp
0º	1,00	1,00
10º	0,70	1,42
20º	0,49	2,04
30º	0,33	3,00
40º	0,22	4,40
45º	0,17	5,83
50º	0,13	7,55

Nesse post, apresentamos os conceitos para que você pudesse entender como surgem as tensões horizontais (empuxos de terra) nos solos e os principais tipos de empuxo de terra e uma maneira simplificada de calcular os mesmos.

Lembrando que existem outras condições que a serem analisadas, por exemplo, solos coesivos, presença de água no solo (sem fluxo) e perfis geotécnicos com várias camadas de solos distintos. Todo esse conteúdo, você pode aprender aqui!

Caso você ainda tenha alguma dúvida, deixa nos comentários que a gente responde!

Não deixe de seguir nosso blog, assinar nossa newsletter, além de acompanhar nosso canal no Youtube e ficar por dentro das novidades!

Até a próxima!