Empuxos de terra: cálculo e aplicações

Se você precisa realizar o dimensionamento de um muro de arrimo ou de uma cortina de contenção, o primeiro passo é determinar a magnitude dos empuxos de terra atuantes na sua estrutura.

Como já abordamos os conceitos iniciais sobre empuxos de terra, nesse post vamos dar mais foco no cálculo dessas tensões horizontais, apresentando situações usuais e práticas.

Preparado para aprender?

Vamos lá!

Teoria de Rankine

Lembrando das considerações feitas para a elaboração da teoria de Rankine apresentado no post anterior, temos:

• O maciço de solo deve ser considerado plano, horizontal e sem coesão (areia pura seca);
• O solo é formado por uma camada única e contínua (homogêneo);
• É desconsiderado o atrito entre o solo e o paramento no plano de contenção;

Para tais situações, já apresentamos as formulações para os coeficientes de empuxos ativo e passivo, que são:

\mathrm{{k_a} = {\tan ^2}(45 - \varphi /2)}

\mathrm{{k_p} = {\tan ^2}(45 + \varphi /2)}

Onde:

• \mathrm{\varphi}: ângulo de atrito interno do solo.

A partir de agora, vamos estudar algumas situações mais usuais e práticas:

• Presença de sobrecarga no solo;
• Presença do nível d’água do solo;
• Solos estratificados (mais de uma camada de solo);
• Solos coesivos;

Presença de sobrecarga no solo

É comum, na prática, termos situações em que o solo a ser contido terá algum tipo de sobrecarga de utilização, seja por alguma edificação ou até mesmo como a construção de rodovias.

Nesse caso, para considerar a influência nos empuxos de terra ocasionados pelo carregamento distribuído da sobrecarga de utilização, devemos “transformar” tal sobrecarga (q) em uma altura equivalente de solo da camada, que chamaremos de h₀.

Ou seja, a tensão vertical no solo ocasionada por q, é equivalente a uma altura de solo h₀:

\mathrm{q = \gamma \cdot {h_0}}

Onde:

• \mathrm{\gamma}: peso específico do solo.

Como já vimos no post anterior, a tensão horizontal em um ponto do interior de um maciço de solo, será a tensão vertical efetiva naquele ponto multiplicada pelo coeficiente de empuxo do solo.

Para calcularmos a tensão horizontal ocasionada por uma sobrecarga, teremos então:

\mathrm{{\sigma _h} = k \cdot \gamma \cdot {h_0}}

Ou simplesmente:

\mathrm{{\sigma _h} = k \cdot q}

Na representação abaixo podemos perceber bem a parcela da tensão horizontal advinda das tensões verticais da sobrecarga de utilização e do peso próprio do solo.

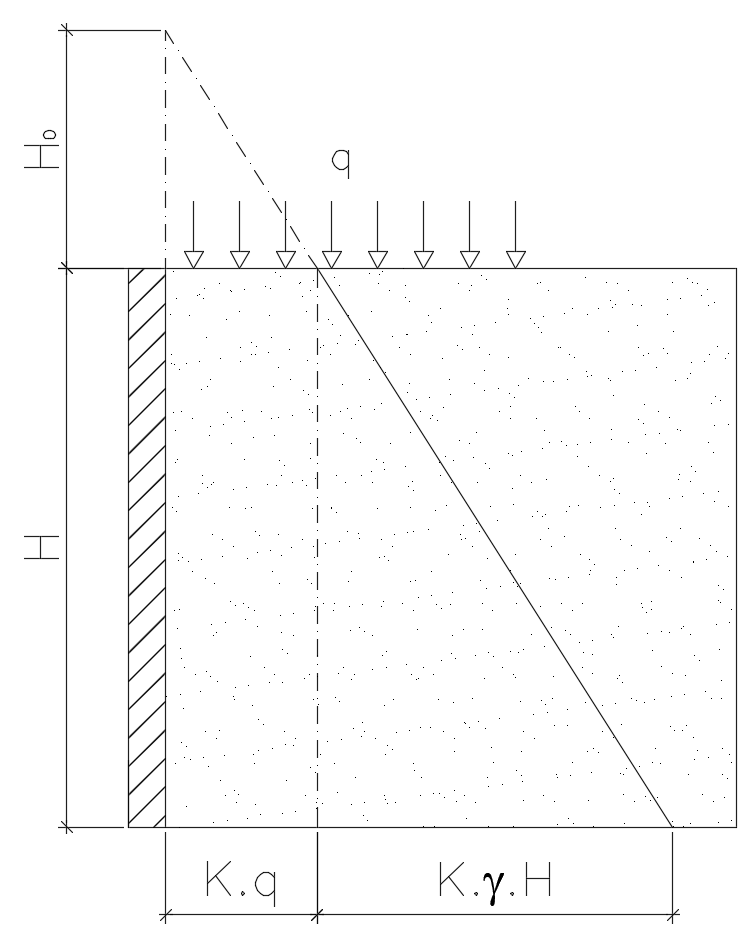
Presença do nível d’água

Outra situação usual é a presença de nível de água no local onde pretende-se construir a contenção.

Vale ressaltar que, como citado no post sobre muros de arrimo, é comum que se tenha um sistema de drenagem nas contenções, de maneira que a água não desenvolva poropressão sobre a estrutura.

Porém, se por algum motivo não é possível realizar um sistema de drenagem nesse paramento ou o mesmo apresentar qualquer problema, devemos considerar o acréscimo de tensão ocasionada pela água.

Lembrando também que, como já citado, as tensões horizontais, e consequentemente os empuxos de terra, são calculadas a partir das tensões verticais EFETIVAS.

Ou seja, para as camadas de solo que estiverem abaixo do nível d’água, devemos utilizar seu peso específico submerso para o cálculo do empuxo.

Então, para camadas de solo que se encontram abaixo do nível d’água, teremos duas parcelas de tensões horizontais, uma ocasionada pelo peso próprio do solo submerso e outra ocasionada pelo peso de água, como podemos ver na figura ilustrativa abaixo.

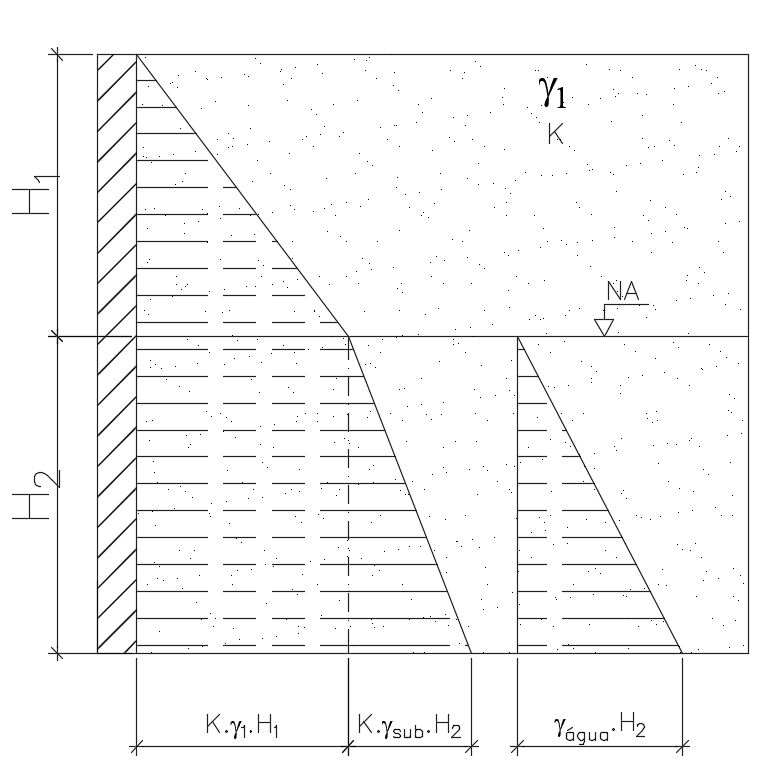
É interessante perceber também, que como a água é um fluido, seu coeficiente de empuxo é igual a 1,0, pois ela transmite em todas as direções o mesmo valor de pressão.

Outra anotação importante é que, geralmente, solos submersos, mesmo que sejam de mesmo material da camada superior ao nível d’água, apresentam ângulo de atrito diferente da camada superior, logo variam também seu coeficiente de empuxo, na figura tal aspecto não é representado!

Presença de solos estratificados

Como os solos tem formação natural, é comum, tanto em solos sedimentares como em solos residuais, serem encontradas várias camadas de solo em um mesmo perfil geotécnico.

Nesse caso, devemos calcular as tensões horizontais individualmente para cada camada de solo. Utilizemos como exemplo, a figura abaixo.

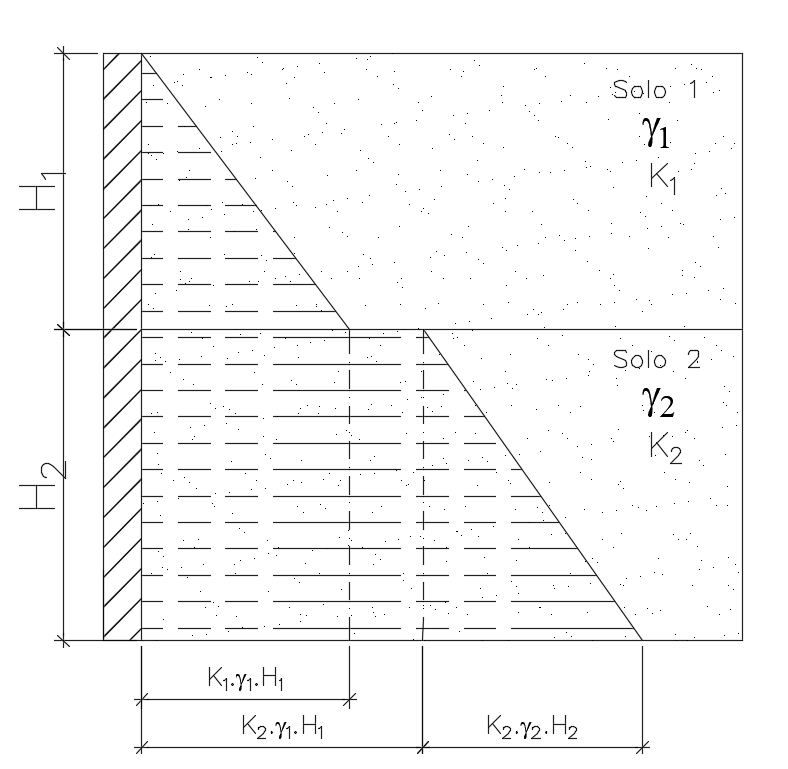
Como cada camada possui um ângulo de atrito interno próprio, elas terão coeficientes de empuxo diferentes entre si.

Perceba que na interface entre as duas camadas de solo, a tensão efetiva vertical é a mesma tanto para o solo 1, quanto para o solo 2.

Logo, nesse ponto ocorrerá uma descontinuidade no gráfico de tensões horizontais. Nesse ponto, são calculados dois valores de tensão horizontal, um com o coeficiente de empuxo do solo 1 e outro com o coeficiente de empuxo do solo 2, conforme pode ser visualizado na ilustração.

Ou seja, no caso de solos estratificados, para a determinação dos empuxos de terra atuantes, apenas devemos ter um cuidado especial no cálculo das tensões horizontais na interface entre diferentes camadas de solo.

Empuxo em solos coesivos

Até agora, todos os exemplos abordados foram para solos não coesivos, ou seja, não levamos em consideração a coesão do solo no cálculo do empuxo, apenas seu ângulo de atrito interno.

Porém, na prática, é bastante usual a presença de argilas ou até mesmo areias argilosas, que por consequência apresentam uma parcela de coesão que não devemos descartar no cálculo dos empuxos.

Como a coesão “trabalha” na resistência ao deslocamento do solo, ela age minorando o empuxo ativo e aumentando o valor do empuxo passivo.

Para o empuxo ativo, temos a seguinte formulação:

\mathrm{{\sigma _h} = {k_a} \cdot \sigma {`_v} - 2 \cdot c \cdot \sqrt {{k_a}}}

Onde:

• c: coesão do solo.

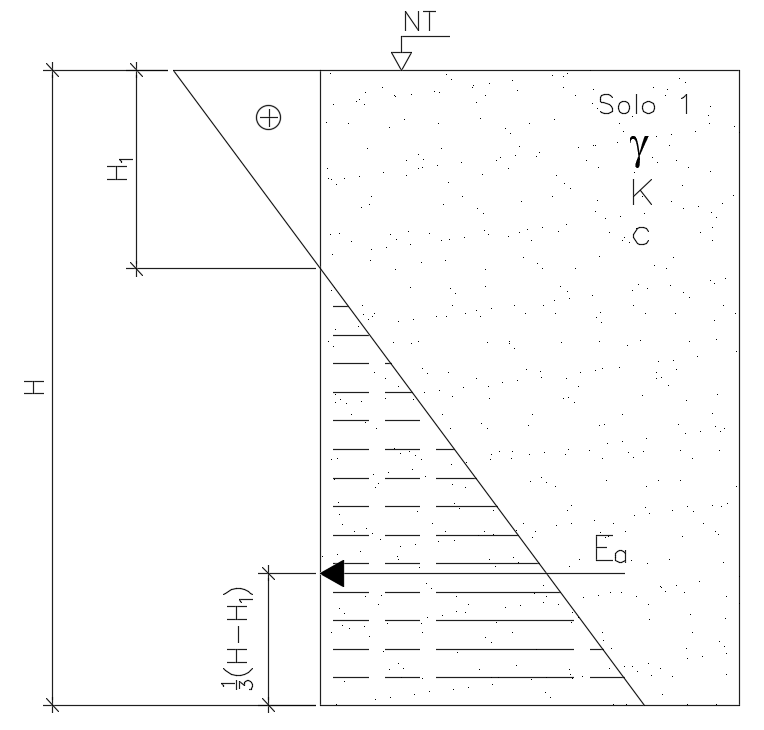
Como podemos perceber pela formulação, para solos em que não há a presença de sobrecarga ou a mesma tenha um baixo valor, a pequenas profundidades, terão tensões horizontais negativas, ou seja, de tração, como pode-se perceber na figura abaixo.

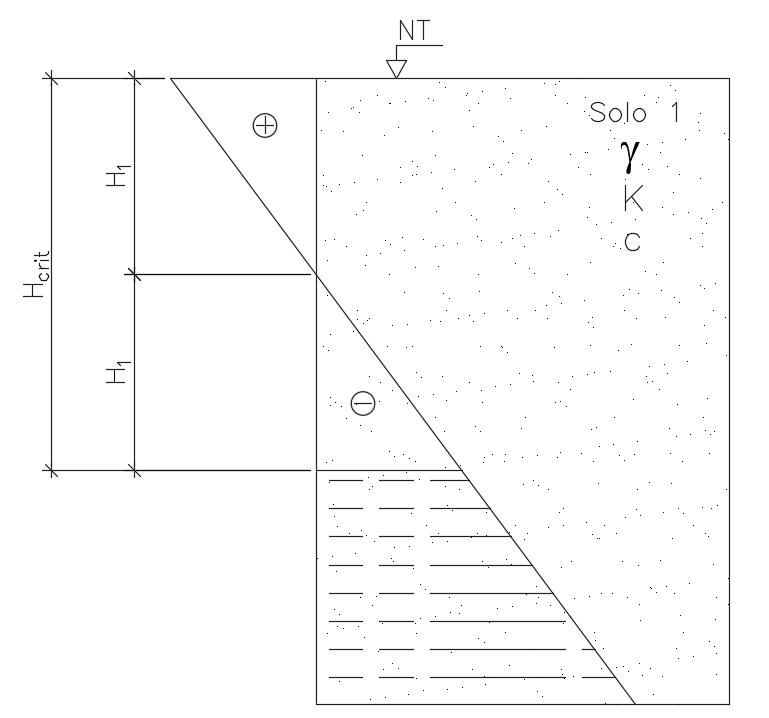
Como o solo não resiste a esforços de tração, nessa região de h₁ é comum a abertura de trincas ou fendas de tração no solo.

Observação sobre solos coesivos

Podemos perceber também, pela figura e por análise matemática, que como o gráfico de tensões horizontais é uma reta, as tensões de tração serão equilibradas por tensões de compressão a uma profundidade de 2h₁.

Essa profundidade em que as tensões de tração se anulam é denominada altura crítica h_crit.

Como até tal altura não dá desenvolvimento de empuxo de terra, teoricamente, é possível realizar corte no solo sem a necessidade de contenção ou escoramento.

Entretanto, é recomendado que na prática, se considere h_crit=h₁.

Logo, para aplicações práticas, devemos considerar o gráfico de tensões horizontais hachurado na figura abaixo para o cálculo do empuxo.

Exemplo resolvido

Para a melhor fixação do conteúdo abordado no post, calcularemos a resultante do empuxo ativo para o exemplo abaixo.

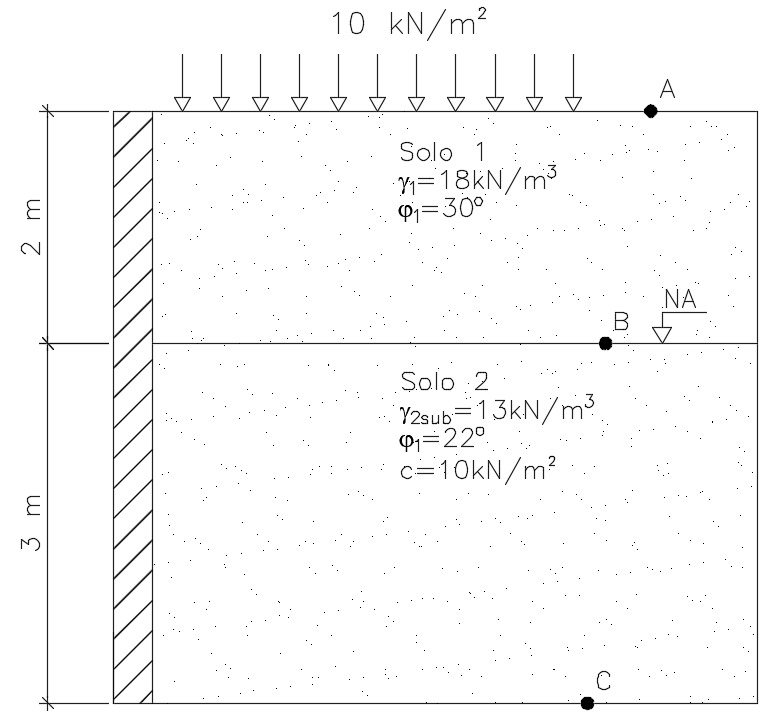
OBS: Para a questão, iremos considerar que a tendência de deslocamento do paramento é para esquerda, logo os empuxos desenvolvidos serão os empuxos ativos.

Resolução

1º Passo

O primeiro passo para a resolução do problema é a determinação das tensões verticais efetivas nos pontos A, B e C, determinados na imagem da questão.

Então, temos que a tensão no ponto A será a da sobrecarga. No ponto B será a soma da sobrecarga com o peso próprio do solo até aquela profundidade e no ponto C será a tensão do no ponto B somada ao peso próprio do solo 2 submerso. Logo:

\mathrm{{\sigma _{vA}} = 10kN/m^2}

\mathrm{{\sigma _{vB}} = 10 + 18 \cdot 2 = 46kN/m^2}

\mathrm{{\sigma _{vC}} = 46 + 13 \cdot 3 = 85kN/m^2}

Agora que já sabemos às tensões nos pontos, devemos determinar o coeficiente de empuxo ativo para os solos 1 e 2. Teremos então, segundo a teoria de Rankine:

\mathrm{{k_{a1}} = {\tan ^2}(45 - 30/2) = 0,33}

\mathrm{{k_{a2}} = {\tan ^2}(45 - 22/2) = 0,45}

2º Passo

De posse desses dados, já podemos calcular a tensão horizontal atuante nos pontos A, B e C. Lembrando que para o ponto B devemos determinar a tensão horizontal para o solo 1 e para o solo 2 e que no cálculo da tensão para o solo 2 devemos considerar a coesão do mesmo e o peso da água no trecho. Temos então:

\mathrm{{\sigma _{hA}} = {\sigma _{vA}} \cdot {k_{a1}} = 10 \cdot 0,33 = 3,3kN/m^2}

\mathrm{{\sigma _{hB1}} = {\sigma _{vB}} \cdot {k_{a1}} = 46 \cdot 0,33 = 15,2kN/m^2}

\mathrm{{\sigma _{hB2}} = {\sigma _{vB}} \cdot {k_{a2}} - 2 \cdot c\sqrt {{k_{a2}}}}

\mathrm{{\sigma _{hB2}} = 46 \cdot 0,45 - 2 \cdot 10\sqrt {0,45} = 7,3kN/m^2}

\mathrm{{\sigma _{hC}} = {\sigma _{vC}} \cdot {k_{a2}} - 2 \cdot c\sqrt {{k_{a2}}} + {\gamma _{água}} \cdot 3}

\mathrm{{\sigma _{hC}} = 85 \cdot 0,45 - 2 \cdot 10\sqrt {0,45} + 30 = 54,8kN/m^2}

Pronto! Agora nós já podemos montar o diagrama de tensões horizontais atuantes na contenção. Temos então o seguinte gráfico:

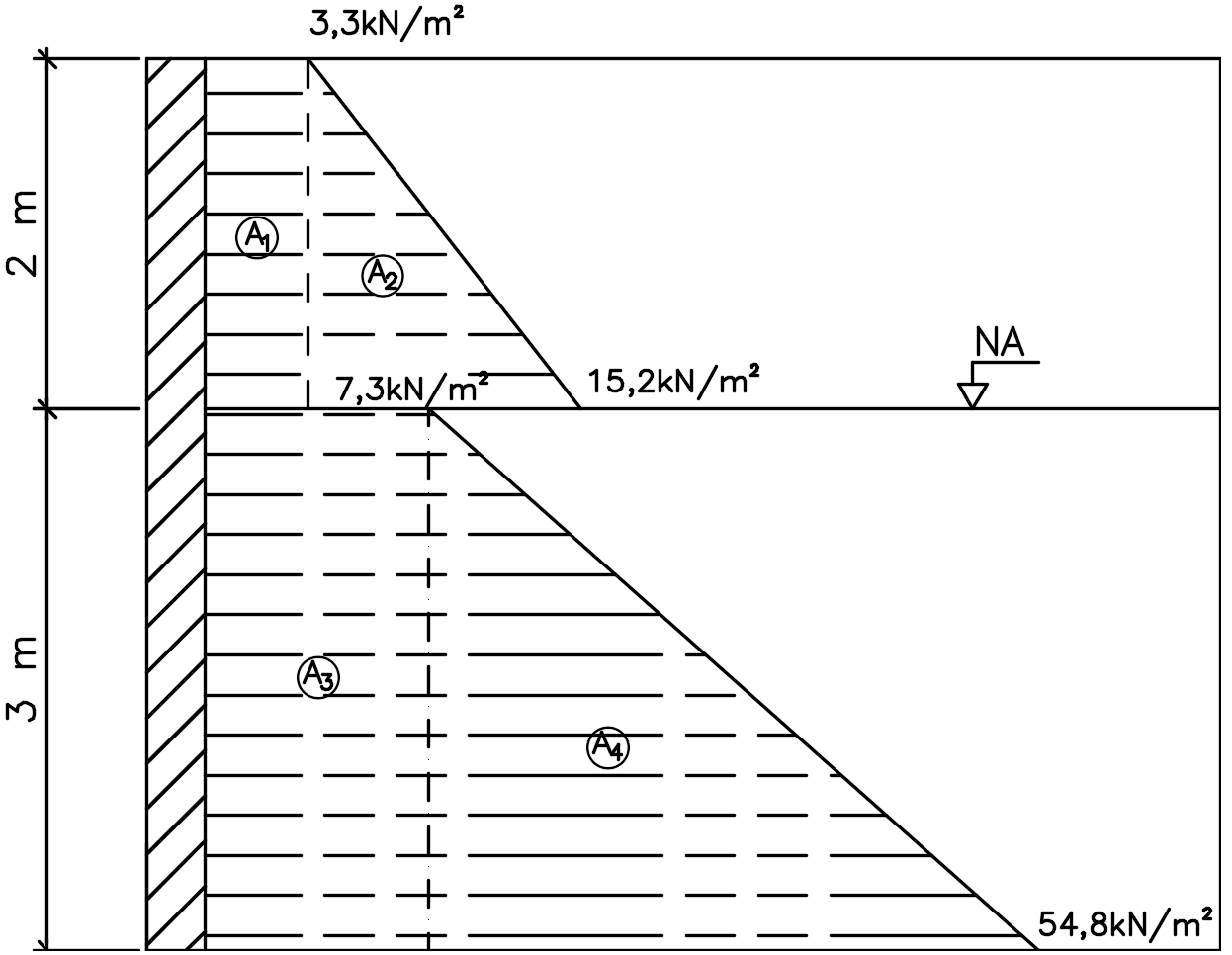
Para realizarmos o cálculo do empuxo resultante, devemos apenas calcular o volume desse prisma de tensões. Considerando a largura do prisma como sendo 1,0 metro, consideração bastante usual no cálculo de contenções, basta calcular a área do gráfico apresentado acima que teremos o empuxo para 1,0 metro de contenção.

3º Passo

Como você já percebeu, eu as áreas foram subdivididas em quatro áreas menores para facilitar tanto o cálculo do empuxo quanto a posição dessa força resultante. Vamos então calcular o empuxo para cada área já demarcada acima.

\mathrm{{E_{A1}} = 3,3 \cdot 2,0 = 6,6kN}

\mathrm{{E_{A2}} = \dfrac{{(15,2 - 3,3) \cdot 2,0}}{2} = 11,9kN}

\mathrm{{E_{A3}} = 7,3 \cdot 3,0 = 21,9kN}

\mathrm{{E_{A4}} = \dfrac{{(54,8 - 7,3) \cdot 3,0}}{2} = 71,3kN}

Pronto, já calculamos o empuxo ativo total atuante na contenção, agora para finalizar, vamos apenas determinar o ponto de aplicação desses empuxos de terra, que será o centroide de cada prisma de tensões. Teremos então o seguinte esquema:

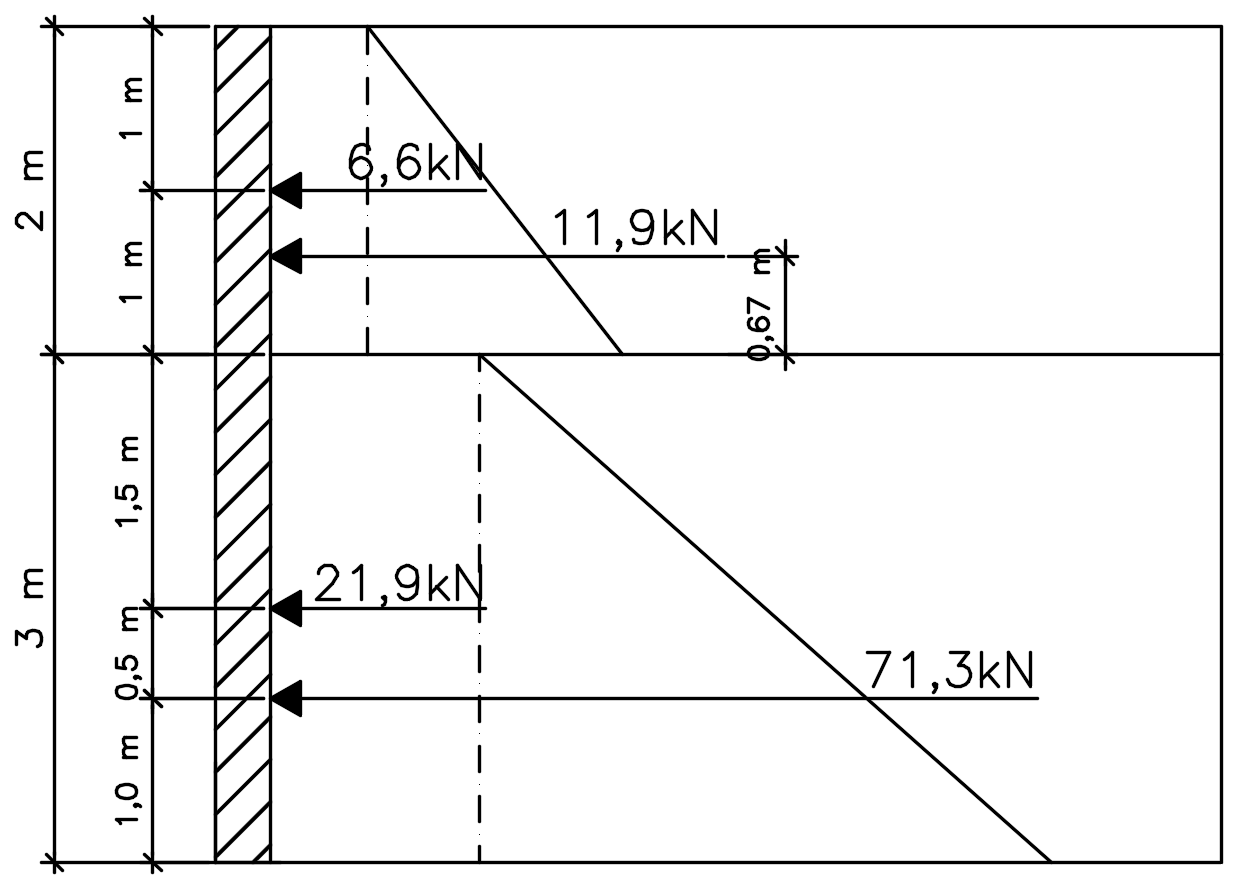
Pronto, viu como não foi tão complicado? Espero que você tenha entendido tudo. Agora que você já aprendeu a calcular os empuxos de terra para os mais diversos tipos de situações, já podemos ir para a etapa do dimensionamento de muros de arrimo!

 

Caso você ainda tenha alguma dúvida, deixa nos comentários que a gente responde!

Não deixe de seguir nosso blog, assinar nossa newsletter, além de acompanhar nosso canal no Youtube e ficar por dentro das novidades!

Até a próxima!