As 5 etapas para dimensionar um muro de gravidade

Você está elaborando um projeto residencial e, ao receber o projeto topográfico do terreno onde a residência será executada, você percebe que há um grande desnível de terra e que você terá que realizar o dimensionamento de um muro de arrimo. E agora, José?

Não precisa se desesperar. É bem mais simples do que você imagina e nós vamos te ajudar!

Nesse post você vai aprender todas as etapas para dimensionar um muro arrimo de gravidade.

Vamos lá?

Etapas do dimensionamento

Como já citado, nesse post vamos nos concentrar no dimensionamento de um muro de arrimo de gravidade.

Lembrando do conceito apresentado no post sobre muros de arrimo: os muros de gravidade, de maneira simplificada, são aqueles que realizam a contenção do maciço de solo por meio de uma combinação entre o seu peso próprio e suas características geométricas.

Ou seja, são estruturas que possuem dimensões mais robustas que os muros de flexão.

Então, podemos dividir o dimensionamento de um muro de gravidade em três etapas:

1. Cálculo dos empuxos (que tenho certeza que você já aprendeu a determinar através dos nossos posts);
2. Pré-dimensionamento do muro de arrimo: nessa etapa, iremos arbitrar as dimensões iniciais do nosso muro de gravidade;
3. Verificação da estabilidade do muro: nessa etapa, iremos fazer as verificações de equilíbrio do muro e das tensões no solo.

Como já tratamos do cálculo do empuxo em posts anteriores, vamos então agora para a etapa de pré-dimensionamento da nossa contenção.

Pré-dimensionamento

Iremos agora apresentar o pré-dimensionamento para as três geometrias de murs de arrimo de gravidade mais utilizados na prática.

Muro de seção retangular

É muito utilizado para pequenas alturas de contenção. Podemos fazer o pré-dimensionamento desse tipo de muro, em pedra argamassada ou concreto ciclópico, a partir das equações na figura abaixo.

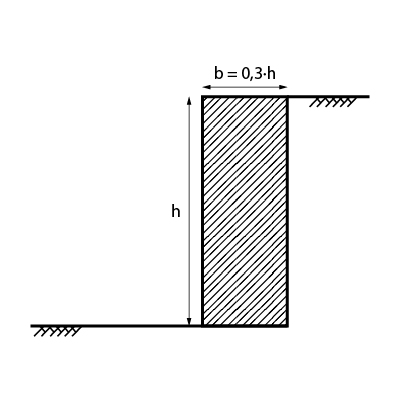
Você pode perceber que, de maneira geral, os pré-dimensionamentos de muros são feitos a partir da altura de solo a ser contida, que geralmente é o dado inicial de que se tem conhecimento.

Muro de seção trapezoidal

Os muros de seção trapezoidal talvez sejam os mais utilizados dos muros de gravidade. O pré-dimensionamento desse tipo de estrutura pode ser feito de acordo com as equações ilustradas nas figuras abaixo.

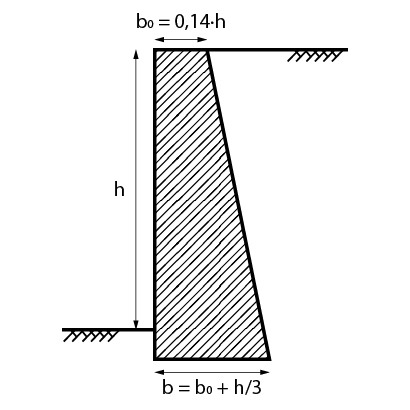
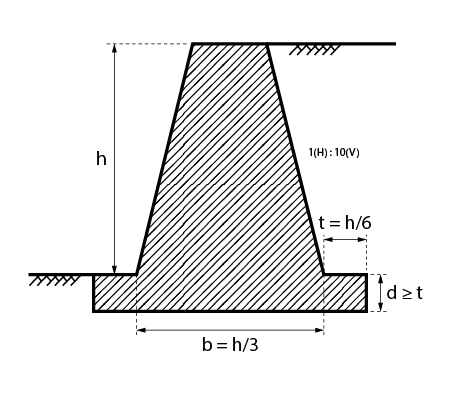
Muro com perfil escalonado

Esse tipo de muro é uma solução muito adotada em estruturas cujo material de construção é a pedra argamassada.

A seguir, é ilustrado um muro com equações usuais no pré-dimensionamento desse tipo de estrutura.

Agora que já temos uma noção das diretrizes para o pré-dimensionamento do nosso muro de arrimo, vamos aprender as condições de estabilidade do muro e de tensão no solo.

Condições de estabilidade

Considere um empuxo ativo atuando sobre um muro de gravidade, ilustrado na figura abaixo.

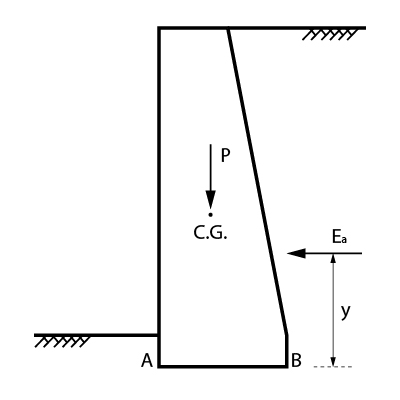
Podemos perceber que o empuxo ativo causa sobre o muro a tendência à dois efeitos: o de deslizamento ao longo da base e o de tombamento do muro, como podemos ver nas figuras abaixo.

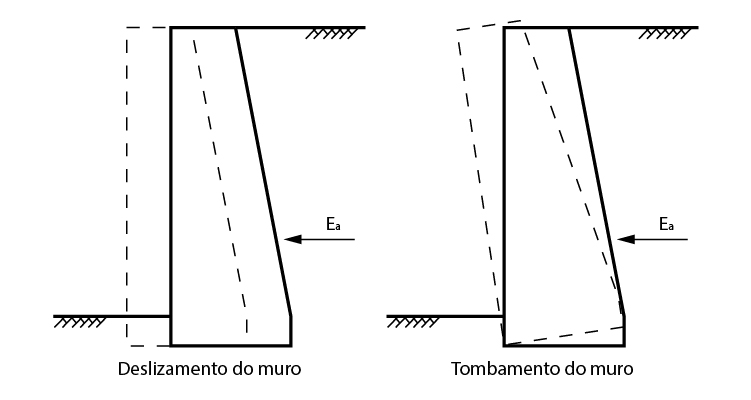
Logo, podemos dizer que para considerarmos o equilíbrio estático do muro, temos as seguintes condições:

\mathrm{\sum {{F_H}} = 0}

\mathrm{\sum {{M_A}} = 0}

Onde:

• F_H: forças horizontais atuantes no muro;
• M_A: momentos em torno do ponto A.

É valido lembrar que além de atender a tais condições de estabilidade, ainda devem ser realizadas duas verificações:

• Verificação das tensões no solo ao longo da base do muro, a fim de garantir que o solo não sofrerá ruptura por compressão;
• Estabilidade global do maciço de solo, considerando o muro de arrimo. Tal verificação será apenas comentada nesse post.

Então, agora vamos às verificações de estabilidade.

Verificação de estabilidade ao deslizamento

Considere a situação ilustrada na figura abaixo.

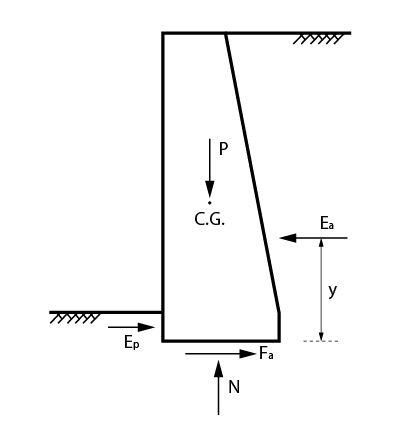
Podemos perceber que a força de empuxo ativo tende a movimentar o muro de arrimo para a esquerda, enquanto o empuxo passivo e a força de atrito entre o solo e o muro, na base da estrutura, resistem à esse movimento se opondo ao empuxo ativo.

Então, a partir de agora, iremos chamar as forças que tendem a causar deslocamento no muro de F_D, no caso F_D=E_a.

E as forças que resistem a esse movimento iremos chamar de F_R.

\mathrm{{F_R} = {E_p} + {F_{at}}}

Em que:

\mathrm{{F_{at}} = N \cdot \mu}

 Onde \mathrm{\mu} é o coeficiente de atrito entre a base do muro de arrimo e o solo.

Para garantir a estabilidade do muro em relação ao deslizamento do mesmo, é utilizado um fator de segurança, geralmente considerado como 1,5, mas podendo ser adotados valores superiores. Logo, temos:

\mathrm{FS = \dfrac{{{F_R}}}{{{F_D}}} \ge 1,50}

Verificação de estabilidade ao tombamento

Em analogia a verificação ao deslizamento, vamos analisar a figura abaixo, com as forças atuantes no muro e seus pontos de aplicação.

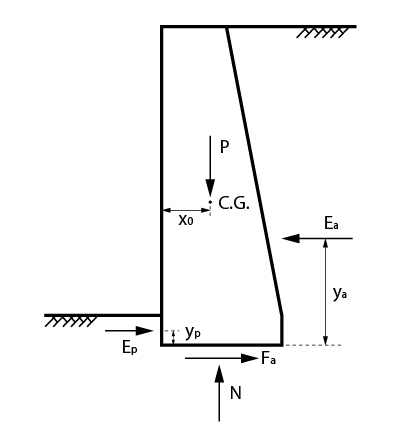
Então, podemos perceber que o empuxo ativo tende a tombar o muro em relação ao ponto A, enquanto o peso do muro e o empuxo passivo causam momentos que resistem a esse tombamento.

Então, chamemos M_T de momento de tombamento e M_R de momento resistente ao tombamento, temos:

\mathrm{{M_T} = {E_a} \cdot {y_a}}

\mathrm{{M_R} = {E_p} \cdot {y_p} + P \cdot {x_g}}

Assim como na verificação ao deslizamento do muro de arrimo, considera-se usualmente um fator de segurança de 1,5 para garantir a estabilidade do muro ao tombamento. Temos então:

\mathrm{FS = \dfrac{{{M_R}}}{{{M_T}}} \ge 1,50}

Capacidade de carga da fundação

A verificação da capacidade de carga na base do muro de arrimo nada mais é do que garantir que não ocorram deformações excessivas no solo na região da base.

Para muros de arrimo de gravidade, costumamos considerar o mesmo como corpo rígido e, assim, as tensões na base, ou fundação, do muro serão distribuídas de maneira linear.

Podemos dizer então, que a base do muro está solicitada à flexocompressão, ou seja, terá a compressão advinda do seu peso próprio e a flexão na base ocasionada pelos empuxos de terra e por uma possível excentricidade do seu peso.

Na figura abaixo, apresentamos, de maneira simplificada como é a distribuição de tensões na base do muro.

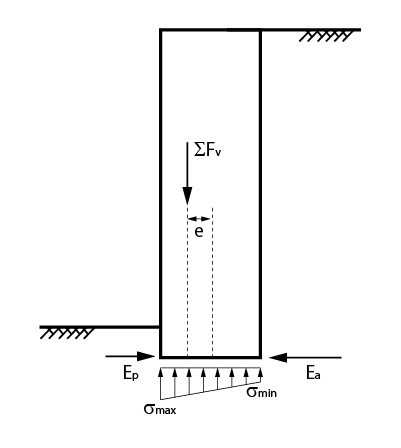
É importante ressaltar que é indicado que toda a base do muro esteja sofrendo compressão. Caso contrário, deve-se redimensionar a base do mesmo a fim de se atender tal indicação.

As tensões na base, como citado anteriormente, são calculadas através das formulações da Mecânica dos Sólidos para flexocompressão normal, ou seja:

\mathrm{\sigma _{máx}=\dfrac{P}{A} +\dfrac{{6 \cdot M}}{{{b^2}}}}

\mathrm{{\sigma _{mín}} = \dfrac{P}{A} - \dfrac{{6 \cdot M}}{{{b^2}}}}

Onde:

• P: somatório das cargas verticais;
• A: área da base da fundação;
• M: somatório dos momentos na base;
• b: dimensão transversal da base do muro;

OBS: as formulações apresentadas acima são válidas para a análise longitudinal de 1,0m de muro de arrimo.

Verificação de ruptura global

Como já falado anteriormente, além das verificações a deslizamento e tombamento do muro, devemos verificar as tensões na base do muro de gravidade e também a possibilidade de ruptura global do maciço de solo considerando a presença da estrutura de contenção.

A verificação do sistema muro-solo em relação à estabilidade global é realizada através de uma análise de ruptura global do maciço.

Se tais conceitos ficaram confusos, considere a figura abaixo. Na figura é ilustrada uma situação de possibilidade de ruptura do maciço. A superfície de escorregamento da cunha de solo é indicada pelo trecho ABC.

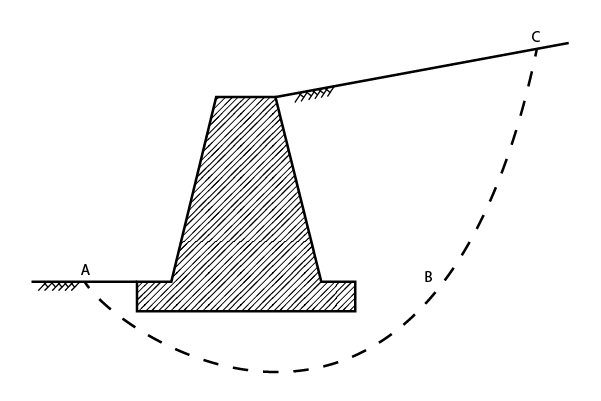
Então, o que precisa ser verificado, através da análise de estabilidade global é justamente o equilíbrio dessa cunha de maciço.

Geralmente, para a determinação do fator de segurança desse tipo de verificação são utilizados os métodos de cálculo de equilíbrio limite, que são os mesmos utilizados na avaliação de estabilidade de taludes, o que será devidamente abordado com mais profundidade em um post futuro.

 

Pois bem, ao fim desse post você já pode dizer que tem o conhecimento para o dimensionamento de um muro de arrimo de gravidade! Para comprovarmos isso, no próximo post iremos dimensionar juntos um muro de gravidade!

 

Mas caso você ainda tenha alguma dúvida, deixa nos comentários que a gente responde!

Não deixe de seguir nosso blog, assinar nossa newsletter, além de acompanhar nosso canal no Youtube e ficar por dentro das novidades!

Até a próxima!