Escada em balanço: como dimensionar a armadura

Antes que você inicie seus estudos sobre dimensionamento de escada em balanço, eu recomendo que revise antes o dimensionamento de escadas usuais. Por se tratar de uma laje em balanço, o dimensionamento se assemelha bastante com a mesma, diferindo basicamente nos carregamentos envolvidos e no detalhamento final.

A seguir você aprenderá como desenvolver o cálculo estrutural de escada em balanço, desde a obtenção das ações até o detalhamento das armaduras.

O modelo 3d abaixo ilustra o tipo de escada que trataremos nessa publicação:

Modelo estrutural de escadas em balanço

O modelo estrutural aplicado para escadas em balanço, conforme já comentado, é basicamente uma laje em balanço. Dessa forma, podemos modelar a mesma através de uma barra engastada em uma extremidade e livre na outra, conforme é apresentado na figura abaixo.

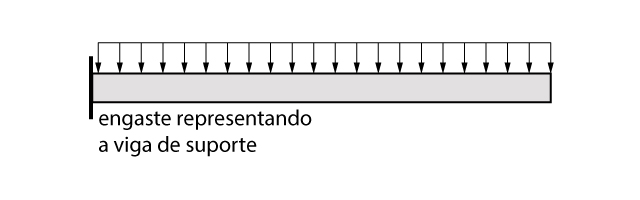
Vale lembrar que, uma vez que o engastamento presente na escada em questão é fornecido por uma viga lateral, devemos verificar essa viga à torção.

Carregamentos

Conforme já comentamos para escadas usuais, os carregamentos que usualmente estão aplicados sobre escadas são: peso próprio da mesma, revestimento, sobrecarga de utilização, ação horizontal e peso próprio sobre o guarda-corpo.

Visto que, o detalhamento desses carregamentos já foram feitos em publicação anterior, não repetirei aqui.

Detalhamento de escadas em balanço

Uma vez que trata de uma escada em balanço, o momento é negativo e traciona a face superior da escada. Assim sendo, a armadura principal, que iremos dimensionar a seguir, é localizada na face superior, conforme ilustra a figura abaixo.

No detalhamento de escadas em balanço, nós iremos distribuir a armação apenas da região superior dos degraus.

Exemplo de aplicação de escada em balanço

A fim de exercitarmos o que estudamos até o momento, vamos calcular uma escada com 1,2 m de largura, 12 cm de espessura, 28 cm de piso (ou passo), 18 cm de espelho, engastada em uma viga de 25 x 60 cm.

Se acaso preferir conteúdos em videoaula, você pode acompanhar a resolução das questões pelo vídeo abaixo!

Cálculo das ações

Em primeiro lugar, vamos calcular o peso próprio da região inclinada. Para isso, é necessário calcular inicialmente uma espessura média, que pode ser calculada pela equação abaixo:

\mathrm{h_m = \dfrac{h}{\dfrac{p}{\sqrt{e^2 + p^2}}} + \dfrac{e}{2}}

\mathrm{\dfrac{0,12}{\dfrac{0,28}{\sqrt{(0,18)^2 + (0,28)^2}}} + \dfrac{0,18}{2} = 0,2 \; m}

\mathrm{g_1 = 0,2 \cdot 25 = 5 \; kN/m^2}

Em segundo lugar, assim como no exemplo anterior, teremos uma carga de revestimento de 1,0 kN/m², uma carga acidental de 2,5 kN/m² (considerando uma escada sem acesso ao público e as cargas decorrentes do parapeito).

Dessa forma, podemos obter o carregamento total distribuído na escada.

\mathrm{p = g_1 + g_2 + q}

\mathrm{p = 5 + 1 + 2,5 = 8,5 \; kN/m^2}

Calculo dos esforços

Primeiramente, é necessário calcular o vão efetivo da laje em balanço. Para isso, iremos considerar, que o apoio da escada em balanço irá até o eixo da viga. Dessa forma, o vão efetivo vale:

\mathrm{l_{ef} = 120 + 12,5 =132,5 \; cm}

Agora vamos utilizar o modelo de barra engastada e livre aplicando o carregamento distribuído calculado anteriormente e as ações aplicadas no parapeito.

Observe que o carregamento distribuído por área foi aplicado linearmente, visto que estamos considerando para o cálculo uma largura de 100 cm.

O momento fletor na extremidade engastada pode ser calculado pela formulação abaixo:

\mathrm{M = - \dfrac{8,5 \cdot (1,32)^2}{2} - 2 \cdot 1,32 - 0,8 \cdot 1,0}

\mathrm{M = -10,85 \; kN \cdot m / m}

Armação necessária para a escada em balanço

Vamos obter agora o momento de cálculo para seguirmos com o dimensionamento. O momento característico calculado anteriormente deve ser multiplicado pelo coeficiente \mathrm{\gamma_f} e pelo coeficiente adicional \mathrm{\gamma_n}, uma vez que se trata de uma laje em balanço.

De acordo com a Tabela 13.2 do item 13.2.4.1 da ABNT/NBR: 6118 (2014), para uma laje em balanço de 12 cm de espessura, teremos  \mathrm{\gamma_n = 1,35}. Assim sendo, o momento de cálculo atuante na laje será:

\mathrm{M_{Sd}=1,4 \cdot 1,35 \cdot 10,85 = 20,51 \; kN \cdot m}

\mathrm{M_{Sd}=2051 \; kN \cdot cm}

O cálculo da área de aço necessária deve ser feito similar ao dimensionamento de uma viga submetida a flexão simples. Para esse exemplo, utilizaremos apenas a Calculadora de Vigas disponível aqui no blog, obtendo assim, uma área de aço \mathrm{As = 2,77 \; cm^2/m}.

[formulario-calculadora-flexao]

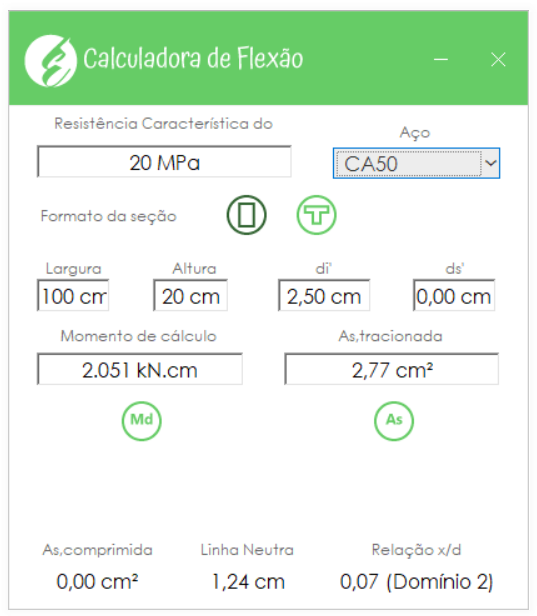
Seleção da armação da escada em balanço

Com uma área de aço necessária de 2,77 cm²/m, iremos distribuir a mesma apenas na região superior dos degraus. Assim, para obter a quantidade de aço em cada degrau, basta multiplicar a área de aço por metro pelo piso do degrau.

\mathrm{A_s = 0,28 \cdot 2,77 = 0,78 \; cm^2}

Você já pensou em detalhar escadas plissadas de concreto armado de uma forma bem simplificada? Dá uma conferida no vídeo abaixo:

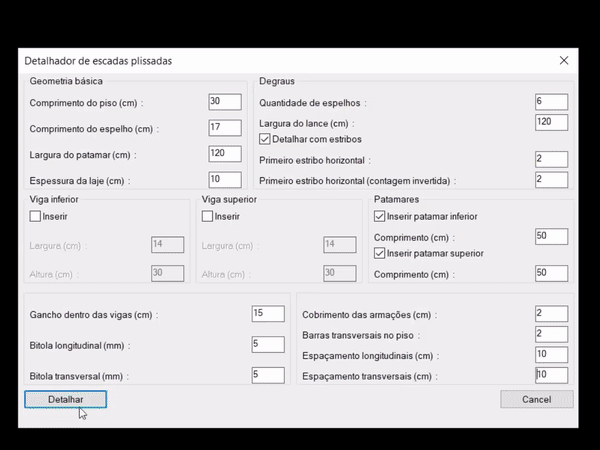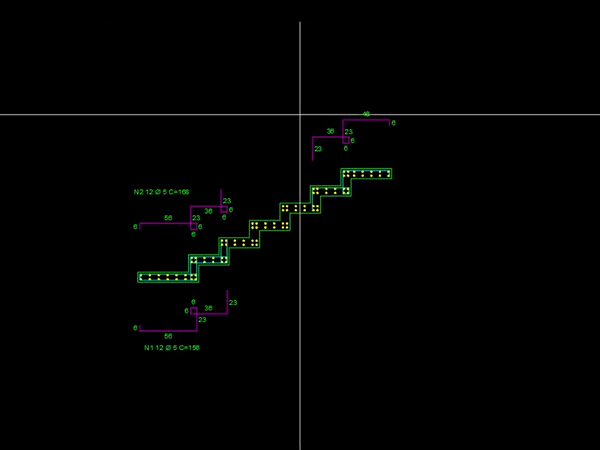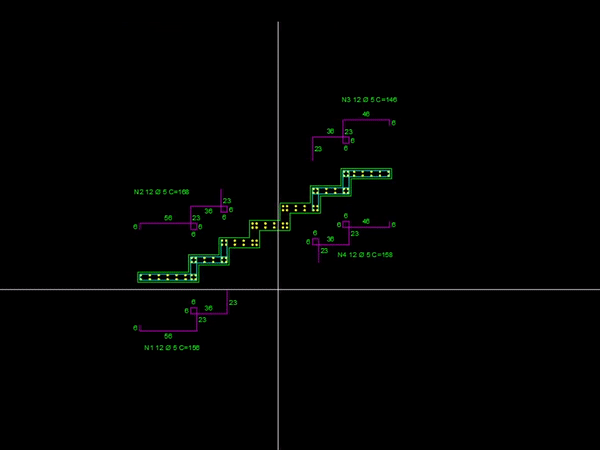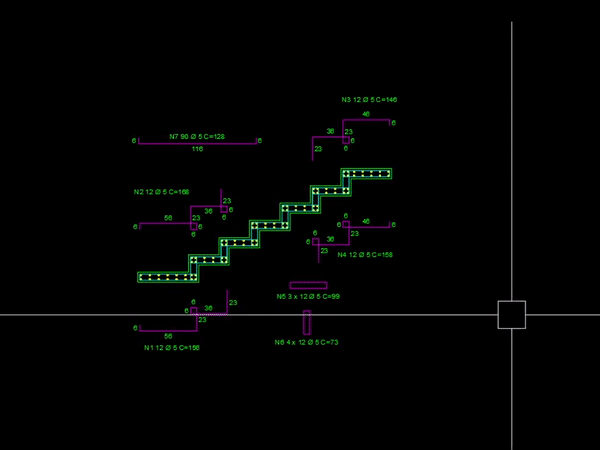
Pois é, essa é uma rotina de detalhamento de escadas plissadas que foi desenvolvida para o AutoCAD. Caso queira conferir mais sobre essa ferramenta basta acessar o link anterior.

Iremos utilizar uma tabela que forneça a área de aço por bitola e quantidade de barras com o intuito de atendermos a área de aço necessária.

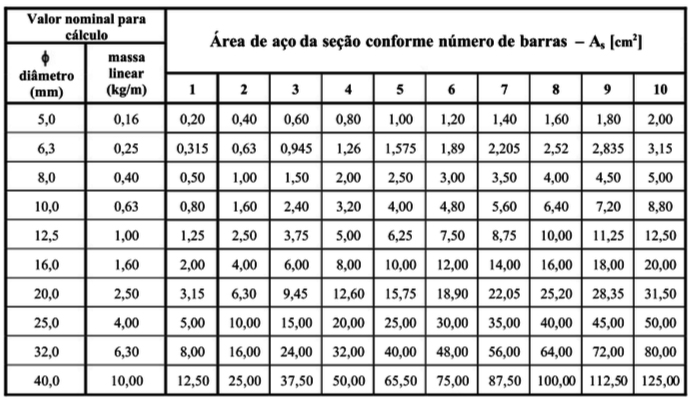
Seguindo a tabela acima, podemos utilizar quatro barras de 8,0 mm, conforme a figura abaixo apresenta.

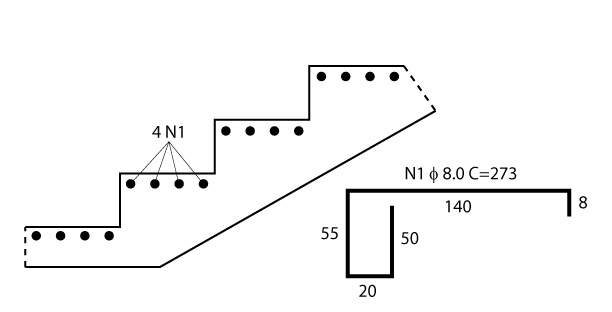
Chegamos ao fim de mais uma publicação sobre dimensionamento de estruturas. Espero que com esse exemplo tenha ficado claro para você como podemos dimensionar uma escada em balanço na viga lateral.

Fico muito feliz que tenha chegado até aqui, parabéns!

---

Fonte:

ARAÚJO, J. M. Curso de Concreto Armado. Rio Grande: Editora Dunas, 2014. v. 4

ASSOCIAÇÃO BRASILEIRA DE NORMAS TÉCNICAS. NBR 6118: Projeto de estruturas de concreto – Procedimento. Rio de Janeiro, 2014.

CARVALHO, R. C.; FIGUEIREDO FILHO, J. R. Cálculo e Detalhamento de Estruturas Usuais de Concreto Armado Segundo a NBR 6118:2014. São Carlos: EdUFSCar, 2014.