Conforme prometido no post anterior sobre o Método Comparativo Direto de Dados de Mercado, iremos agora aprender sobre um dos métodos de tratamento de dados: o tratamento científico por meio da inferência estatística utilizando a regressão linear, com base nos procedimentos normatizados pela ABNT NBR 14.653: Avaliação de Bens – Parte 2: Imóveis Urbanos (anexo A).
Mas, antes disso tudo, iremos fazer um breve revisão para relembrarmos alguns conceitos básicos relacionados à estatística.
E se você caiu aqui de paraquedas e quer aprender sobre avaliações de imóveis desde o início, temos outros posts pra te ajudar nisso:
Agora, vamos ao que interessa?
Introdução à estatística
Antes de aprendermos a avaliar um imóvel utilizando o tratamento científico por inferência estatística, precisamos revisar alguns conceitos básicos relacionados à estatística para que tenhamos um entendimento completo de todos os termos utilizados no decorrer desse post.
Se preferir ver esse assunto em vídeo, clique na imagem abaixo.
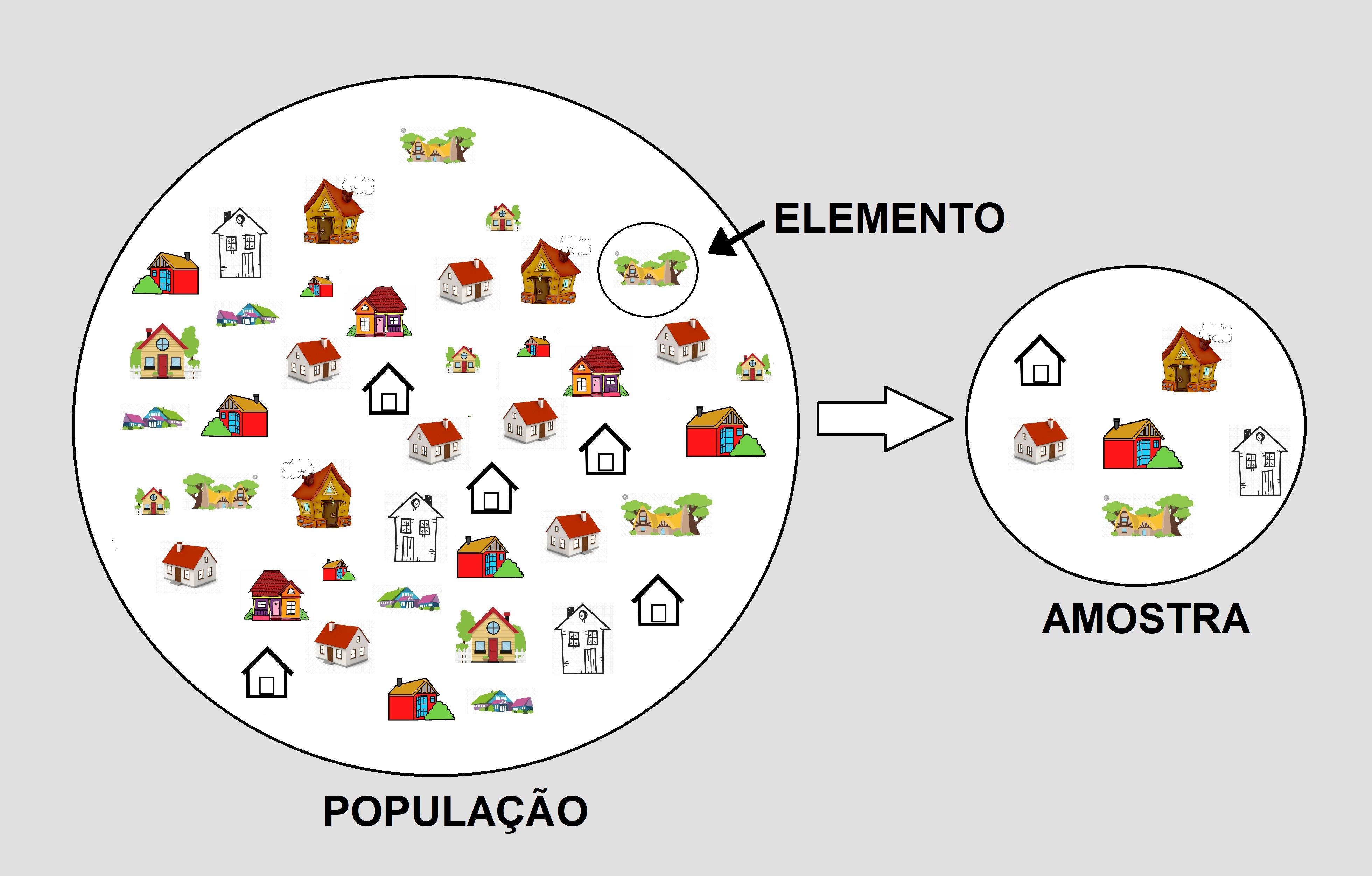
O primeiro conceito básico que veremos agora é a diferença entre População, Amostra e Elemento, que utilizamos bastante ao tratarmos do Método Comparativo Direto de Dados de Mercado. Vejamos:
População, Amostra e Elemento
População é o conjunto de elementos com pelo menos uma característica em comum, enquanto amostra é um subconjunto de uma população utilizada para efeito de estudo estatístico.
Em outras palavras, amostra é apenas uma pequena parte de uma população e é utilizada quando se deseja analisar o comportamento de uma população, sem necessariamente analisar todos os seus elementos. E, para isso, é feito um levantamento estatístico.
Medidas de tendência central
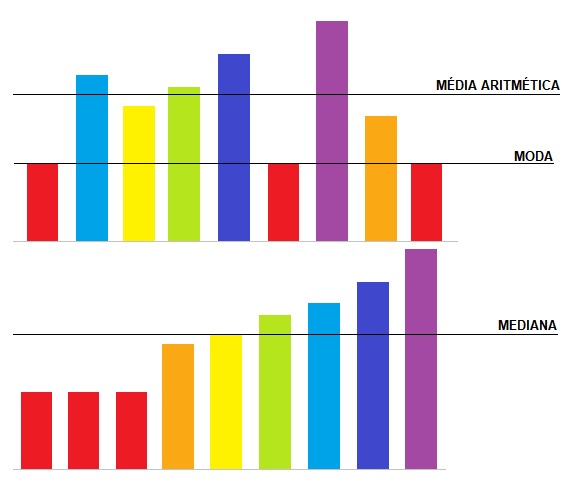
O próximo conceito que veremos são as medidas de tendência central, que servem para localizar a distribuição dos dados brutos com o objetivo de resumir um conjunto de elementos em um único número que representa a amostra.
Existem 3 tipos de medida de tendência central, são eles:
Média aritmética (\mathrm{\overline{x}})
A média aritmética nada mais é que a razão entre a soma de todos os elementos de um conjunto e o total de elementos.
Moda (\mathrm{M_o})
A moda é o valor que aparece com mais frequência em um conjunto de dados, ou seja, o valor que aparece um maior número de vezes.
Mediana (\mathrm{M_d})
Por fim, a mediana é o valor de centro de um conjunto de dados. Desse modo, para calculá-la, os elementos devem, primeiramente, ser ordenados na ordem crescente. Então, se o número de elementos for par, a mediana é a média dos dois valores centrais, se não, a mediana é o valor que está exatamente no meio.
Estimadores de dispersão
Amplitude (A)
Amplitude nada mais é que a diferença entre dois extremos, ou seja, entre o maior e o menor elemento do conjunto.
Variância (\mathrm{{S^2}_x})
A variância, por sua vez, é definida como a média dos quadrados das diferenças entre os valores em relação a sua própria média e é expressa, matematicamente, como:
\mathrm{{S^2}_x=\dfrac{Σ(x_i-\overline{x})^2}{n-1}}
Onde:
- \mathrm{{S^2}_x} é a variância;
- \mathrm{x_i} é o elemento na posição i;
- \mathrm{\overline{x}} é a média aritmética da amostra;
- n é o número de elementos da amostra.
Desvio Padrão (\mathrm{S_x})
Em poucas palavras, o desvio padrão é a raiz positiva da variância e indica o quanto os elementos da amostra se afastam da média central.
\mathrm{{S^2}_x=\sqrt{\dfrac{Σ(x_i-\overline{x})^2}{n-1}}}
Onde:
- \mathrm{{S}_x} é o desvio padrão;
- \mathrm{x_i} é o elemento na posição i;
- \mathrm{\overline{x}} é a média aritmética da amostra;
- n é o número de elementos da amostra.
Coeficiente de variação (\mathrm{{CV}_x})
Por último, o coeficiente de variação é a razão entre o desvio padrão e a média aritmética.
\mathrm{CV_x=\dfrac{S_x}{\overline{x}}}
Onde:
- \mathrm{{CV}_x} é o coeficiente de variação;
- \mathrm{{S}_x} é o desvio padrão;
- \mathrm{\overline{x}} é a média aritmética da amostra.
Distribuição Normal
A distribuição normal é uma das distribuições de probabilidade mais utilizadas para modelar fenômenos naturais e é representada pela curva de Gauss, que possui a forma abaixo:
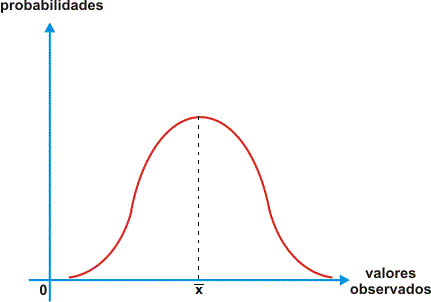
Desse modo, a partir da distribuição normal é possível inferir a probabilidade de uma observação assumir um valor entre dois pontos quaisquer, que equivale à área do gráfico compreendida entre esses dois pontos.
Regressão linear
Pois bem, engenheiros, após essa pequena revisão, já estamos prontos para adentrarmos no tratamento científico de dados de imóveis por meio da regressão linear e começaremos, então, pelos seus procedimentos básicos, normalizados pela NBR 14653-2.
Vale lembrar que tarefa de avaliar um imóvel por meio da inferência estatística não é algo muito simples e, por isso, recomendamos o uso de softwares específicos para lhe ajudar nisso, como, por exemplo, Excel, SAB, SisDEA, entre outros.
Procedimentos básicos
Se preferir ver esse assunto em vídeo, clique na imagem abaixo.
1. Número mínimo de elementos
Considerando que até chegar aqui você já tenha escolhido as variáveis que irão compor seu modelo de avaliação pelo Método Comparativo Direto, agora você precisa ir ao mercado de imóveis e coletar os dados que irão compor sua amostra.
Desse modo, para evitar a micronumerosidade, o número mínimo de dados efetivamente utilizados no modelo (para atingir o grau de fundamentação mínimo) deve obedecer ao seguinte critério:
\mathrm{n=3(k+1)}
Além disso,
n ≤ 30 ⇒ ni ≥ 3
30 < n ≤ 100 ⇒ ni ≥ 10%n
n > 100 ⇒ ni ≥ 10
Onde:
- n é o número mínimo de dados efetivamente utilizados;
- k é o número de variáveis independentes utilizadas no modelo;
- ni é o número de dados de mesma característica, no caso de utilização de variáveis dicotômicas e variáveis qualitativas expressas por códigos alocados ou códigos ajustados.
Tabela 1 – Grau de fundamentação do modelo em relação ao número de elementos (item 2)
2. Gráfico de dispersão
Coletados todos os dados pertinentes ao seus modelo, devemos agora analisar o comportamento do gráfico da variável dependente em relação a cada variável independente.
Essa etapa é muito importante para que possamos entender a relação que cada variável tem sobre o preço unitário do seu imóvel avaliando e, é claro, para verificar a tendência, intensidade e as dispersão dos dados e a forma funcional da curva.
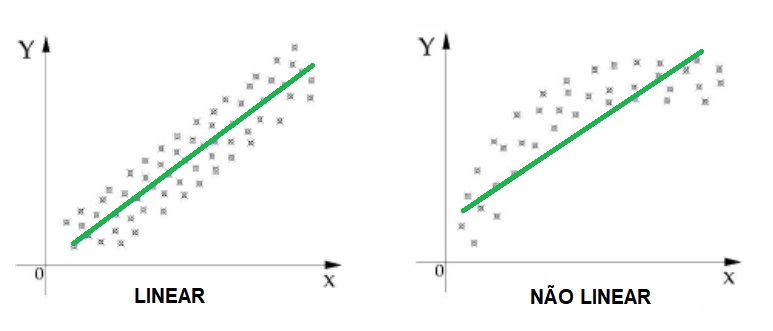
3. Linha de tendência
Analisada a dispersão do gráfico, você deverá traçar a linha de tendência para esse conjunto de dados para que seja possível inferir a influência da variável independente sobre a variável dependente, que é quantificada pelo coeficiente de correlação de Pearson, a seguir.
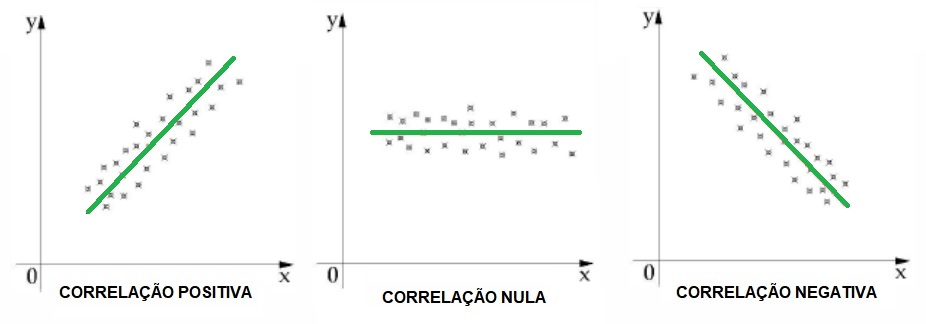
4. Coeficiente de correlação de Pearson (r)
Como já dito, esse coeficiente expressa o grau da relação ou nível de influência de uma variável sobre outra e pode variar entre 0 e 1, conforme a tabela abaixo.
Dessa fora, podemos observar que, quanto maior é a correlação entre uma variável independente e uma variável dependente, melhor é o grau de explicação do modelo.
Tabela 2 – Coeficiente de correlação de Pearson
| r=0 | relação nula |
| 0<r≤0,3 | relação fraca |
| 0,3<r≤0,7 | relação média |
| 0,7<r≤0,9 | relação forte |
| 0,9<r<1 | relação fortíssima |
| r=1 | relação perfeita |
Esse coeficiente é extremamente importante ao analisarmos os dados de mercado porque ele é muito sensível a valores extremos. Ou seja, quando coletamos imóveis com valores anormais em relação à média do mercado imobiliário, o coeficiente de correlação pode alterar significativamente.
Por isso, para que sua avaliação seja satisfatória, é sempre importante identificar e corrigir dados que estejam associados a eventos anormais, que são aqueles que estão mais afastados da linha de tendência.
Além disso, esse coeficiente também é usado para analisar a correlação entre duas variáveis independentes.
Bom, mas se é independente não tem correlação, certo?
Isso mesmo, pessoal, o ideal é que as vaiáveis independentes escolhidas para os seus modelo não tenham nenhuma relação entre si (r=0), mas, na prática, isso é bem impossível de ocorrer. Por isso, é indicado que a correlação entre duas variáveis independentes não ultrapasse o valor de 0,80.
5. Teste de validação da variável independente
Esse teste é representado pela estatística T e mede o erro da estimativa do parâmetro, ou seja, o erro de cada variável independente para o modelo.
A tabela abaixo fornece os valores máximos admissíveis para o erro de uma variável independente, de acordo com o Grau desejado.
Tabela 3 – Grau de fundamentação do modelo em relação ao nível de significância do modelo (item 5)
| Descrição | Grau | ||
| III | II | I | |
| Nível de significância (somatório do valor das duas caudas) máximo para a rejeição da hipótese nula de cada regressor (teste bicaudal) | 10% | 20% | 30% |
6. Teste de significância do modelo
O próximo passo da análise dos dados diz respeito ao teste de significância do seu modelo, que indica quantas vezes um Grau de Liberdade da Regressão é maior do que um Grau de Liberdade dos Resíduos.
Para ficar ainda mais claro, significância é, basicamente, o oposto de confiança e é considerada um procedimento para verificar a discrepância de uma hipótese estatística em relação aos dados observados, ou seja, está relacionada ao erro.
Pois bem, esse teste de significância é representado pela estatística F, que é a relação entre (média dos quadrados da regressão/média dos quadrados dos resíduos) e compara o F tabelado com o F calculado e, para que o modelo seja aceito, F calculado deve ser maior que F tabelado.
A tabela abaixo fornece os valores máximos admissíveis para F de significação, de acordo com o Grau desejado.
Tabela 4 – Grau de fundamentação do modelo em relação ao nível de significância (item 6)
| Descrição | Grau | ||
| III | II | I | |
| Nível de significância máximo admitido nos demais testes estatísticos realizados | 1% | 2% | 5% |
7. Preço estimado
Satisfeitos todos os testes de significância, iremos agora estimar o preço unitário do imóvel avaliando por meio da equação fornecida pela linha de tendência extraída do gráfico de dispersão dos dados, substituindo as variáveis independentes pelas características referentes ao avaliando.
8. Intervalo de confiança
O intervalo de confiança é uma amplitude de valores derivados da estatística, que tem a probabilidade de conter o valor de um parâmetro populacional desconhecido.
O seu cálculo é usado para analisarmos a faixa de preços unitários em que o imóvel avaliando está inserido, considerando um certo grau de confiança (geralmente adota-se 80%). Para isso, utiliza-se a média aritméticas dos preços unitários dos elementos da amostra.
Desse modo, para o cálculo dos limites de confiança, segundo a Teoria Estatística das Pequenas Amostras (n<30), temos:
\mathrm{x_{máx}=\overline{x}+\dfrac{t_{(1-α/2;n-1)}\cdot{S}}{\sqrt{n}}}
\mathrm{x_{mín}=\overline{x}-\dfrac{t_{(1-α/2;n-1)}\cdot{S}}{\sqrt{n}}}
Onde:)
- \mathrm{x_{máx}} é o limite superior do intervalo de confiança;
- \mathrm{x_{mín}} é o limite inferior do intervalo de confiança;
- \mathrm{\overline{x}} é a média aritmética dos dados;
- S é o desvio padrão da amostra;
- \mathrm{t_{(1-α/2;n-1)}} é o valor percentual para a distribuição “t” de Student para um grau de liberdade n-1 e um dado grau de confiança c, sendo α=1-c;
- n é o número de elementos da amostra.
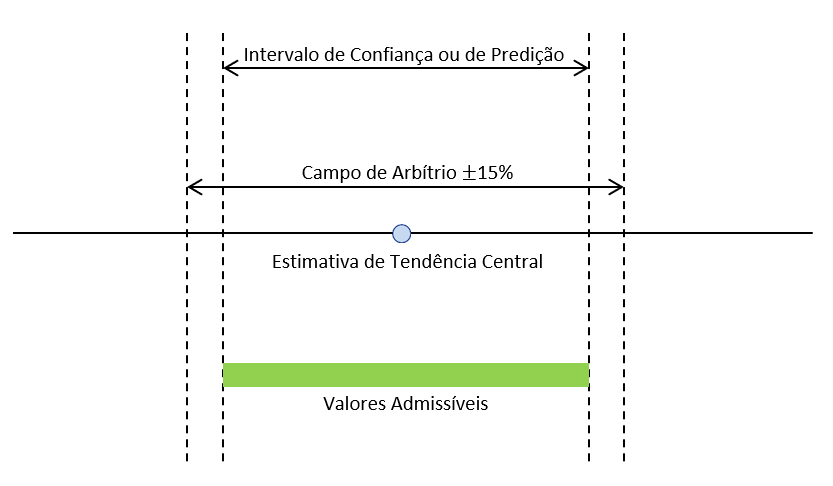
9. Campo de arbítrio
O campo de arbítrio é outro tipo de intervalo, que engloba uma variação de mais ou menos 15% em torno do preço estimado.
Assim como no intervalo de confiança, no campo de arbítrio podemos arbitrar o valor do bem, desde que justificado pela existência de características próprias não contempladas no modelo, limitado ao intervalo de confiança.
10. Enquadramento do modelo
Por fim, a última etapa da regressão linear é o enquadramento do modelo de acordo com o Grau de Precisão e o Grau de Fundamentação e, para isso, usaremos as tabelas fornecidas pela NBR 14653-2, no anexo A.
Primeiramente, utilizaremos a tabela 5 abaixo e classificaremos cada um dos itens no grau adequado, lembrando que o Grau III vale 3 pontos, o II vale 2 pontos e o I vale 1 ponto.
Tabela 5 – Grau de fundamentação para regressão linear
Feito isso, podemos enquadrar o laudo na tabela 6 seguinte referente ao Grau de Fundamentação.
Tabela 6 – Critérios de enquadramento do laudo no Grau de Fundamentação
| Grau | III | II | I |
| Pontos mínimos | 16 | 10 | 6 |
| Itens obrigatórios no grau correspondente | 2, 4, 5 e 6 no Grau III e os demais no mínimo no Grau II | 2, 4, 5 e 6 no mínimo no Grau II e os demais no Grau I | Todos, no mínimo no Grau I |
Por último, basta enquadrar o laudo (considerando a não extrapolação dos dados) na tabela 7, referente ao Grau de Precisão do modelo. Sendo a Amplitude calculada por:
\mathrm{A=\dfrac{[(P_{est}–x_{mín})+(x_{máx}-P_{est})].100}{P_{est}}}
Onde:
- A é a amplitude (%);
- \mathrm{P_{est}} é o preço estimado (R$/m²);
- \mathrm{x_{máx}} é o limite superior do intervalo de confiança (R$/m²);
- \mathrm{x_{mín}} é o limite inferior do intervalo de confiança (R$/m²).
Tabela 7 – Critério de enquadramento do laudo no Grau de Precisão
| Descrição | Grau | ||
| III | II | I | |
| Amplitude do intervalo de confiança de 80% em torno do valor central da estimativa | ≤30% | ≤40% | ≤50% |
Agora, para ficar ainda mais fácil de assimilar, eu recomendo que você exercite tudo que aprendemos até aqui. E é claro que eu preparei um exercício prático comentado para que não restem mais dúvidas sobre isso!
.
Pois bem engenheiros, essas foram algumas considerações a respeito da Regressão Linear para Avaliação de Imóveis. E para te ajudar ainda mais, preparamos um e-Book gratuito sobre Avaliação de Imóveis.
[ebook-avaliacao-imoveis]É claro, no entanto, que esse universo é muito mais amplo do que conseguimos abordar em um e-Book.
Então, se você quiser se aprofundar mais nessa área, sugiro que conheça o curso online Formação de Peritos Judiciais em Avaliação de Imóveis de um dos nosso parceiros, o professor Fernando Sarian, que tem mais de 17 anos de experiência na área.
Nesse curso, você irá conhecer as norma vigentes, aprenderá sobre o Avaliação Imobiliária e, o melhor de tudo, aprenderá a elaborar seu próprio laudo técnico de avaliação. Tudo isso dando um enfoque especial na área pericial e nas legislações de interesse.
Ficou curioso? É só clicar aqui.
Dito isso, ficamos por aqui e se gostou você gostou, não deixa de seguir a gente no Instagram e também no Youtube para receber todas as novidades.
E se ainda ficou com alguma dúvida, deixe aqui nos comentários. Até o próximo post!
Fonte:
ASSOCIAÇÃO BRASILEIRA DE NORMAS TÉCNICAS. NBR 14653-1: Avaliação de bens – Parte 1: Procedimentos gerais. Rio de Janeiro, 2019. 31 p.
ASSOCIAÇÃO BRASILEIRA DE NORMAS TÉCNICAS. NBR 14653-2: Avaliação de bens – Parte 2: Imóveis urbanos. Rio de Janeiro, 2011. 62 p.
BRASIL. Ministério do Planejamento, Desenvolvimento e Gestão. Secretaria do Patrimônio da União. Manual de Avaliação. Brasília: SPU, 2017.
CARNEIRO NETO, Waldemiro. Inferência estatística Aplicada: Avaliação de Imóvel Urbano. Teresina: IPOG, 2018.
.

Engenheira Civil pela Universidade Federal do Piauí, engenheira de obra, perita judicial e pós-graduanda em Avaliação, Auditoria e Perícias de Engenharia.





Excelente artigo, um blog fácil de entender, parabéns e continue com o bom trabalho!!
Muito obrigada, continuaremos!!!
Boa tarde Dandara! Tudo bem?
Preciso informar o endereço das minhas amostras no laudo de avaliação, ou só o informante é aceito?
Obrigado
Boa tarde, José. Informar o endereço não é obrigatório, por norma, mas é interessante fazer isso no laudo.
Excelente publicação, parabéns. Tem pouco conteúdo e até mesmo cursos acerca da aplicação da inferência na avaliação de imóveis.
Muito obrigada, Alberto!
Boa tarde Dandara, primeiramente, parabéns pelo conteúdo.
Poderia indicar um software para calculo da inferência estatística para Avaliação de Imóveis?
Desde já agradeço a atenção.
Obrigada, Fábio, fique à vontade.
SIMPLES E PRÁTICO. BEM EXPLICADO.TENHO 20 ANOS DE AVALIAÇÃO NA CAIXA E SEMPRE APRENDENDO.
Muito obrigada Silvio, fico muito feliz em ajudar!
O conteúdo e apresentação do vídeo está muito bom mesmo, parabéns.
Agora, eu ficaria imensamente agradecido se pudesse ter acesso aos dados coletados referente à pesquisa dos imoves, para exercitar e entender como chegar nos resultados da avaliação por inferência estatística, será que poderia obter esses dados?
SDS Ivo Ferreira
Oi, Ivo, fico muito feliz que gostou! Então, todos os dados utilizados no exercício estão no post de exercício. Vale lembrar que são apenas dados hipotéticos, tudo bem?
Parabéns pela video e pela explicação.
Tenho uma dúvida com relação aos dados da amostra, mais precisamente os preços coletados na pesquisa.
No tratamento por fatores utilizamos o fator oferta onde reduzimos os valores coletados em 10% (negociação). Na inferencia estatistica devemos aplicar esse fator ou trabalha com os valores cheios?
Clevis, se você achar necessário aplicar o fator oferta na sua amostra, mesmo se tratando de inferência estatística, não há problema algum, desde que esteja devidamente justuficado.