No nosso post anterior sobre Inferência Estatística aplicada a Avaliação de Imóveis, explicamos quais os procedimentos básicos para realizar o Tratamento Científico de Dados de Mercado, utilizando a Regressão Linear. Se não leu ainda, recomendamos que dê uma olhada clicando aqui.
Agora, vamos solidificar o que foi aprendido sobre Avaliação de Imóveis até o momento. Para tanto, propomos um exercício hipotético de uma avaliação de imóvel urbano pelo Método Comparativo Direto de Dados de Mercado, através de tratamento científico por Inferência Estatística.
Confira abaixo!
Exemplo prático
Pretende-se avaliar para venda um apartamento localizado em um condomínio fechado na cidade de Teresina-PI, com área de 75 m² e distante 2 Km do centro comercial da cidade.
Características complementares do imóvel avaliando:
Está localizados no quarto pavimento de um dos 8 blocos existentes no condomínio (não há elevadores), possui padrão normal de acabamento e a seguinte divisão interna:
- 3 quartos, sendo 1 suíte;
- Banheiro social;
- Cozinha;
- Sala de estar;
- Varanda;
- 1 vaga de garagem.
Elementos da amostra do mercado:
| DADOS | ÁREA PRIVATIVA (m²) | Nº DE SUÍTES | PREÇO DE VENDA UNITÁRIO (R$/m²) |
| 01 | 91,00 | 0,00 | 2967,03 |
| 02 | 64,00 | 1,00 | 4218,75 |
| 03 | 60,00 | 1,00 | 4500,00 |
| 04 | 68,00 | 0,00 | 3970,59 |
| 05 | 89,00 | 0,00 | 3033,71 |
| 06 | 110,00 | 1,00 | 2454,55 |
| 07 | 73,00 | 1,00 | 3698,63 |
| 08 | 100,00 | 1,00 | 2700,00 |
| 09 | 60,00 | 0,00 | 4500,00 |
| 10 | 59,00 | 1,00 | 4576,27 |
| 11 | 74,00 | 0,00 | 3648,65 |
| 12 | 76,00 | 1,00 | 3552,63 |
| MÉDIA | 77,00 | 0,58 | 3651,73 |
RESOLUÇÃO:
Antes de começarmos, vale ressaltar que os passos aqui apresentados foram realizados com o auxílio do software Microsoft Office Excel.
Então, caso queira mais informações a respeito das ferramentas e comandos utilizados nesse exercício, clique aqui.
Passo 01: Verificar o número mínimo de elementos
A partir dos dados fornecidos, podemos inferir que a variável dependente em questão é o preço unitário e que existem duas variáveis independentes para este modelo: número de suítes e área privativa.
Desse modo, o número mínimo de dados efetivamente utilizados no modelo (para atingir o grau de fundamentação mínimo) deve obedecer ao seguinte critério:
\mathrm{n=3(k+1)=3(2+1)=9\:elementos}
Como a amostra para esse modelo possui 12 elementos, podemos concluir que o grau de fundamentação mínimo foi atingido e, dessa forma, a amostra pode ser utilizada.
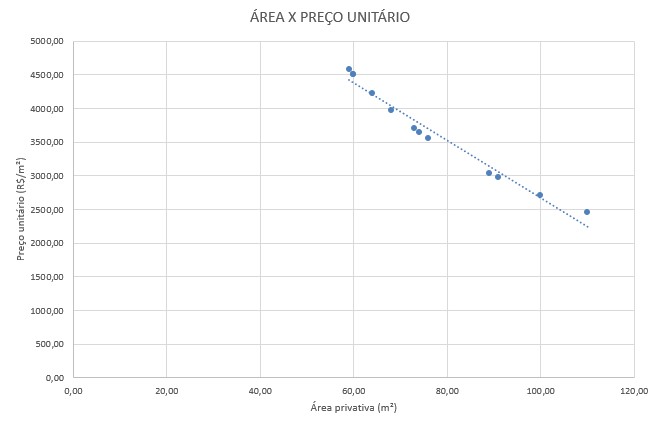
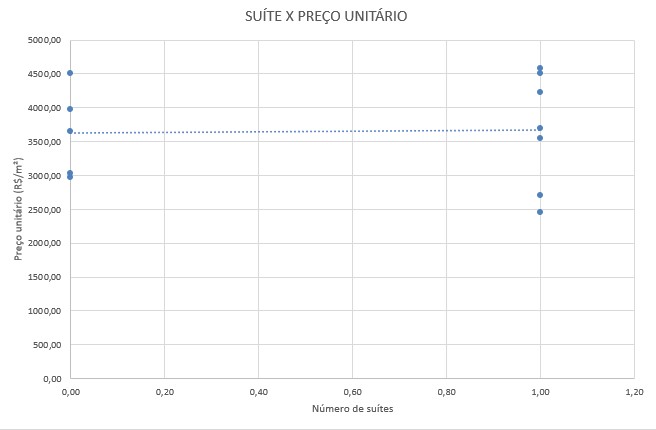
2. Plotar os gráficos de dispersão
Após analisar os gráficos de dispersão e traçar as linhas de tendência, é possível deduzir que:
1) Para a área privativa, a dispersão dos dados é linear e possui tendência negativa com grande inclinação, o que significa que imóveis de maior área possuem preço unitário menor;
2) Para o número de suítes, a dispersão dos dados não é linear e possui tendência quase nula e ligeiramente positiva, mostrando que o número de suítes possui pouquíssima influência sobre o preço unitário do imóvel, para este modelo;
Passo 03: Analisar a correlação entre as variáveis
A correlação entre as variáveis é representada pelo coeficiente de Pearson (r) e expressa o nível de influência de uma variável sobre outra e pode variar entre 0 e 1.
Dessa forma, quanto maior é a correlação entre uma variável independente e uma variável dependente, melhor é o grau de explicação do modelo.
Já em relação às variáveis independentes, o ideal é que a correlação entre elas seja próximo de zero mas, quando isso não for possível, seu valor não deve ultrapassar 0,80.
Sabendo disso, ao analisarmos a matriz de correlação abaixo, podemos inferir que:
1) A correlação entre as variáveis independentes área e suítes (vermelho) é próxima de zero;
2) A correlação entre as variáveis suíte e preço (verde) é próxima de zero, ou seja, é fraca;
3) A correlação entre as variáveis área e preço (verde) é próxima de 1, ou seja, é fortíssima.
Tabela 1 – Matriz de correlação
| ÁREA PRIVATIVA (m²) | Nº DE SUÍTES | PREÇO DE VENDA UNITÁRIO (R$/m²) | |
| ÁREA PRIVATIVA (m²) | 1 | ||
| Nº DE SUÍTES | 0,031368217 | 1 | |
| PREÇO DE VENDA UNITÁRIO (R$/m²) | -0,985031565 | 0,033379925 | 1 |
Passo 04: Realizar o teste de validação da variável independente
Esse teste é representado pela estatística T e mede o erro da estimativa do parâmetro, ou seja, o erro de cada variável independente para o modelo.
Para esse passo, o valor que devemos coletar é o “valor-P”, presente na tabela ANOVA de Regressão, que é o seguinte:
\mathrm{(valor-P)_{área}=1,79838273213172\cdot{10^{-08}}=0,0000018}% ≤ 30% ⇒ OK!
\mathrm{(valor-P)_{suíte}=0,258432078134073=25,84}% ≤ 30% ⇒ OK!
Podemos notar que o erro da variável suíte, apesar de estar dentro do limite máximo de 30%, é significavelmente maior que o erro da variável área, reforçando a ideia de que a utilização da variável suíte não contribuiu positivamente para o modelo.
Como alternativa, a variável independente suíte pode e dever ser excluída para otimizar o modelo de regressão e elevar o grau de fundamentação do laudo.
No entanto, a título de exercício, iremos prosseguir a avaliação preservando a variável suíte.
Passo 05: Realizar o teste de significância do modelo
O próximo passo da análise dos dados diz respeito ao teste de significância do modelo, que indica quantas vezes o Grau de Liberdade da Regressão é maior do que o Grau de Liberdade dos Resíduos.
Para esse passo, o valor que devemos buscar é o “F de significação”, presente na tabela ANOVA de Regressão, que é o seguinte:
\mathrm{F\:de\: significação=6,84421625156359\cdot10^{-08}=0,0000068}% ≤ 10% ⇒ OK!
Passo 06: Estimar o preço unitário do avaliando
Satisfeitos todos os testes de significância, iremos agora estimar o preço unitário do imóvel avaliando por meio da equação fornecida pelo modelo de regressão, substituindo as variáveis independentes pelas características referentes ao avaliando.
PREÇO UNITÁRIO (R$/m²) = 6900,1553 + (-42,8817) * ÁREA PRIVATIVA (m²) + 91,6580 * Nº DE SUÍTES
PREÇO UNITÁRIO = 6900,1553 + (-42,8817) * 75 + 91,6580 * 1
PREÇO UNITÁRIO = 3775,69 R$/m²
Passo 07: Calcular o intervalo de confiança
O intervalo de confiança é usado para analisarmos a faixa de preços unitários em que o imóvel avaliando está inserido, considerando o grau de confiança de 80%.
Para seu cálculo necessitamos, primeiramente, calcular o desvio padrão dos preços unitários dos dados da amostra, que é: S=733,54 R$/m².
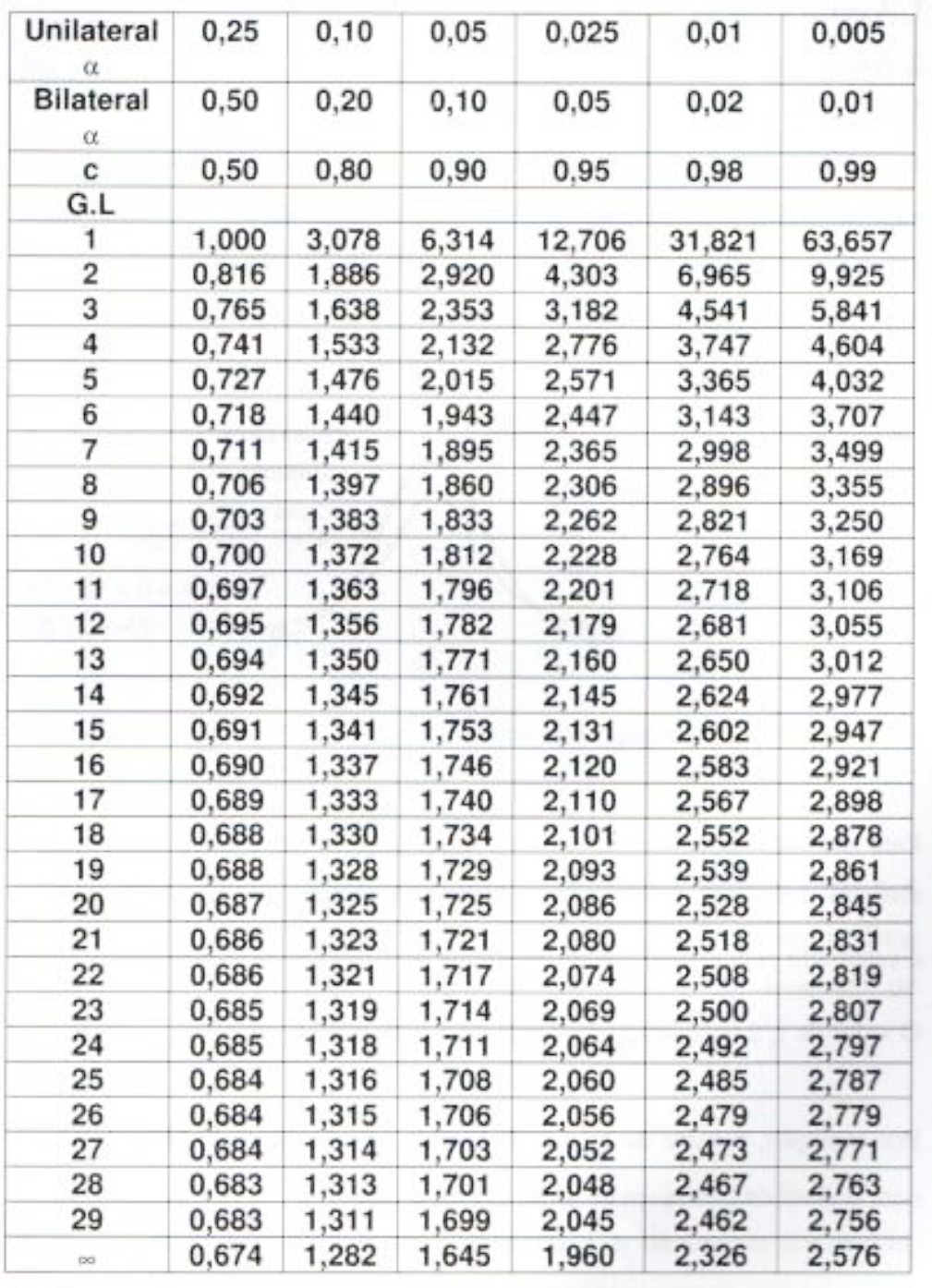
Além disso, necessitamos também do valor de \mathrm{t_{1-α/2;n-1}}, que, de acordo com a tabela abaixo, é \mathrm{t_{0,90;11}=1,363}
Tabela 2 – Valor percentual para a distribuição “t” de Student para grau de liberdade n-1 e grau de confiança “c”
Por fim, para o cálculo dos limites de confiança, temos:
\mathrm{x_{máx}=\overline{x}+\dfrac{t_{1-α/2;n-1}\cdot{S}}{\sqrt{n}}}
\mathrm{x_{máx}=3651,73+\dfrac{1,363\cdot{733,54}}{\sqrt{12}}=3940,45\:R\$/m^2}
\mathrm{x_{mín}=\overline{x}-\dfrac{t_{1-α/2;n-1}\cdot{S}}{\sqrt{n}}}
\mathrm{x_{mín}=3651,73-\dfrac{1,363\cdot{733,54}}{\sqrt{12}}=3363,02\:R\$/m^2}
Isso significa dizer que qualquer valor que esteja dentro do intervalo de confiança pode ser utilizado para determinar o valor unitário do imóvel avaliando, com 80% de confiança.
Logo, o preço estimado por meio da equação do modelo é adequado para representar o valor do avaliando.
Passo 08: Calcular o campo de arbítrio
O campo de arbítrio é outro tipo de intervalo, que engloba uma variação de mais ou menos 15% em torno do preço estimado, portanto:
\mathrm{x_{máx}=P_{est}\cdot(1+0,15)}
\mathrm{x_{máx}=3775,69\cdot{1,15}=4342,04\:R{\$}/m^2}
\mathrm{x_{mín}=P_{est}\cdot(1-0,15)}
\mathrm{x_{máx}=3775,69\cdot{0,85}=3209,33\:R{\$}/m^2}
Esse segundo intervalo é usado para arbitrar o valor do avaliando, caso haja extrapolação do modelo, ou seja, caso o preço estimado não esteja inserido no intervalo de confiança.
Dessa forma, no campo de arbítrio é possível arbitrar o preço unitário do avaliando, desde que justificado pela existência de características próprias não contempladas no modelo.
No entanto, como não houve extrapolação nos resultados, o campo de arbítrio não será utilizado.
Passo 09: Enquadrar o modelo
Por fim, a última etapa do exercício será o enquadrar do modelo de acordo com o Grau de Precisão e o Grau de Fundamentação. Para isso, usaremos as tabelas abaixo, fornecida pela NBR 14653-2.
Primeiramente, utilizaremos a tabela 3 abaixo e classificaremos cada um dos itens no grau adequado, lembrando que o Grau III vale 3 pontos, o II vale 2 pontos e o I vale 1 ponto.
Tabela 3 – Grau de fundamentação para regressão linear
Feito isso, o resultado da pontuação foi de 12 pontos. No entanto, devido ao erro da varíavel suíte > 20 %, teremos que enquadrar o laudo no Grau de Fundamentação I.
Tabela 4 – Critérios de enquadramento do laudo no Grau de Fundamentação
| Grau | III | II | I |
| Pontos mínimos | 16 | 10 | 6 |
| Itens obrigatórios no grau correspondente | 2, 4, 5 e 6 no Grau III e os demais no mínimo no Grau II | 2, 4, 5 e 6 no mínimo no Grau II e os demais no Grau I | Todos, no mínimo no Grau I |
Por último, basta enquadrarmos o laudo na tabela abaixo, referente ao Grau de Precisão do modelo. Sendo a Amplitude calculada por:
\mathrm{A=\dfrac{[(P_{est}-x_{mín})+(x_{máx}-P_{est})]\cdot{100}}{P_{est}}}
\mathrm{A=\dfrac{[(3775,69-3363,02)+(3940,45-3775,69)]\cdot{100}}{3775,69}}
\mathrm{A=15,29\:{\%}}
Tabela 5 – Critério de enquadramento do laudo no Grau de Precisão
| Descrição | Grau | ||
| III | II | I | |
| Amplitude do intervalo de confiança de 80% em torno do valor central da estimativa | ≤30% | ≤40% | ≤50% |
Dessa forma, o laudo está enquadrado no Grau de Precisão III.
Resultado
De posse de todos os cálculos realizados, o valor de mercado do apartamento avaliando foi de R$ 283.176,61, podendo ser arredondado (em até 1% para mais ou menos) para o valor de R$ 285.000,00, resultando em uma Avaliação de Grau de Fundamentação I e Grau de Precisão III.
Ah, para exercitarem ainda mais, sugiro que resolvam esse mesmo exemplo retirando a variável suíte do modelo e me contem aqui nos comentários qual resultado vocês obtiveram.
Pois bem, avaliadores, esse foi um breve exemplo hipotético de como dever ser feita uma avaliação de imóveis urbanos, na prática, por meio da Inferência Estatística. E para te ajudar ainda mais, preparamos um e-Book gratuito sobre Avaliação de Imóveis.
[ebook-avaliacao-imoveis]É claro, no entanto, que esse universo é muito mais amplo do que conseguimos abordar em um e-Book.
Então, se você quiser se aprofundar mais nessa área, sugiro que conheça o curso online Formação de Peritos Judiciais em Avaliação de Imóveis de um dos nosso parceiros, o professor Fernando Sarian, que tem mais de 17 anos de experiência na área.
Nesse curso, você irá conhecer as norma vigentes, aprenderá sobre o Avaliação Imobiliária e, o melhor de tudo, aprenderá a elaborar seu próprio laudo técnico de avaliação. Tudo isso dando um enfoque especial na área pericial e nas legislações de interesse.
Ficou curioso? É só clicar aqui.
Dito isso, ficamos por aqui e se gostou você gostou, não deixa de seguir a gente no Instagram e também no Youtube para receber todas as novidades.
E se ainda ficou com alguma dúvida, deixe aqui nos comentários. Até o próximo post!
Fonte:
ASSOCIAÇÃO BRASILEIRA DE NORMAS TÉCNICAS. NBR 14653-1: Avaliação de bens – Parte 1: Procedimentos gerais. Rio de Janeiro, 2019. 31 p.
ASSOCIAÇÃO BRASILEIRA DE NORMAS TÉCNICAS. NBR 14653-2: Avaliação de bens – Parte 2: Imóveis urbanos. Rio de Janeiro, 2011. 62 p.
BRASIL. Ministério do Planejamento, Desenvolvimento e Gestão. Secretaria do Patrimônio da União. Manual de Avaliação. Brasília: SPU, 2017.
CARNEIRO NETO, Waldemiro. Inferência estatística Aplicada: Avaliação de Imóvel Urbano. Teresina: IPOG, 2018.
.

Engenheira Civil pela Universidade Federal do Piauí, engenheira de obra, perita judicial e pós-graduanda em Avaliação, Auditoria e Perícias de Engenharia.