Geometria de sapatas sob cargas centradas: exercício

Se você chegou nesse post, eu imagino que já tenha estudado a teoria por trás da obtenção da geometria de sapatas isoladas. Correto?
Caso não tenha estudado ainda, recomendo bastante que acesse primeiro os conceitos para o cálculo das dimensões de sapatas isoladas.

Agora vamos a resolução de um exercício para fixar esse aprendizado.

Exemplo aplicado

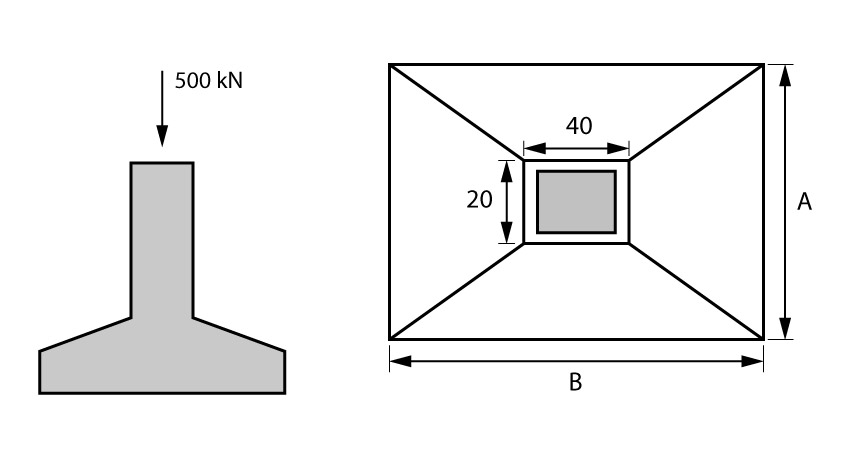
Neste exemplo vamos calcular as dimensões de uma sapata que recebe um pilar de 20 x 40 cm, submetido a uma carga centrada de 500 kN (valor característico). A tensão admissível do solo para essa situação é de 300 kN/m² (0,30 MPa). Além disso vamos considerar que o concreto seja C30 (resistência característica de 30 MPa) e também que a armadura longitudinal do pilar seja composta de barras de 10 mm.

Caso você prefira ver essa resolução em vídeo é só conferir abaixo.

Cálculo da área de base de sapatas

Inicialmente, observamos que a ação informada de 500 kN não está separada em permanente e variável. Assim sendo, iremos considerar o coeficiente \mathrm{K_{maj}=1,05} para considerar o peso próprio da sapata nos cálculos.

Vamos agora calcular a área de base necessária para que a tensão atuante seja inferior a tensão admissível:

\mathrm{S_{sap} = \dfrac{1,05 \cdot N_{gk+qk}}{\sigma_{adm}}}

\mathrm{S_{sap} = \dfrac{1,05 \cdot 500}{300}}

A partir da equação acima obtemos uma área de base necessária de 1,75 m².

Obtenção das dimensões de base

A partir da área de base, é possível obter as duas dimensões da base da sapata ao considerar os balanços (abas) iguais (\mathrm{A - a_p = B - b_p}) nas duas direções:

\mathrm{B = \dfrac{b_p - a_p}{2} + \sqrt{ \dfrac{(a_p - b_p)^2}{4} + S_{sap} }}

\mathrm{B = \dfrac{40 - 20}{2} + \sqrt{ \dfrac{(20 - 40)^2}{4} + 17500 }}

Resolvendo essa equação chegamos em \mathrm{B = 142,6 \; cm}, que podemos aproximar o múltiplo de 5 superior, no caso, 145 cm.

Sabendo agora o valor da maior dimensão e conhecendo também a relação \mathrm{A - a_p = B - b_p}, é possível calcular o valor de A:

\mathrm{A = 145 - 40 + 20}

\mathrm{A = 125 \; cm}

Ao mesmo tempo, poderíamos apenas perceber que, seguindo a ideia de abas iguais, como a diferença entre as dimensões do pilar nas duas direções é de 20 cm, a diferença entre as dimensões da sapata nas duas direções também será de 20 cm. Logo, como a maior dimensão da sapata é de 145 cm, para garantir as abas iguais a menor dimensão será de 125 cm.

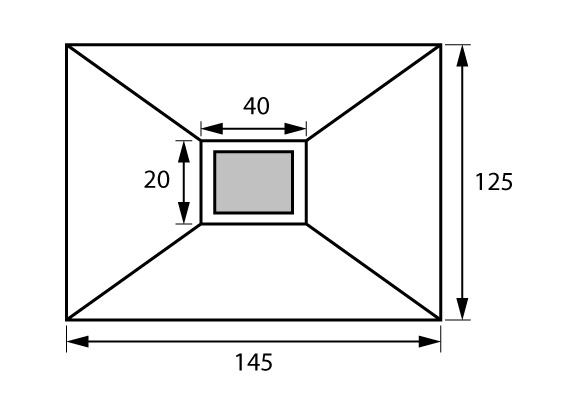
Cálculo da altura das sapatas

Chegamos então em uma sapata de 125 x 145 cm de base. O próximo passo é a obtenção da altura da sapata e da altura do rodapé a fim de garantir a rigidez da mesma. Uma vez que as abas são iguais nas duas direções, a verificação da rigidez da sapata pode ser realizada em qualquer uma das direções.

\mathrm{h \geq \dfrac{A - a_p}{3}}

Aplicando a condição de rigidez para as dimensões já encontradas, obtemos a altura necessária.

\mathrm{h \geq \dfrac{125 - 20}{3}}

\mathrm{h = 35 \; cm}

Como o resultado será inferior a 40, utilizaremos uma altura mínima recomendada de 40 cm.

Outra verificação que devemos fazer é se a altura encontrada é suficiente para a ancoragem da armadura longitudinal do pilar.

\mathrm{d> l_b}

Para uma barra de 10 mm e um concreto com resistência característica de 10 mm, obtemos um comprimento básico de ancoragem de \mathrm{l_b = 34 \; cm}.

[interesse-fundacoes-rasas]

Considerando que a altura útil seja \mathrm{d = h-5 = 35 \; cm}, esta altura será suficiente para ancoragem da armadura do pilar.

O próximo passo será o cálculo da altura do rodapé, nesse caso seguiremos com as formulações abaixo:

\mathrm {h_0 = \left\{ \begin{array}{ll} 20 \; cm \\ \dfrac{h}{3} \end{array} \right. }

\mathrm {h_0 = \left\{ \begin{array}{ll} 20 \; cm \\ \dfrac{40}{3} = 13,33 \; cm \end{array} \right. }

Dessa forma, seguiremos com uma altura de rodapé de 20 cm.

Nesse momento, já calculamos todas as dimensões da sapata. Em suma, obtemos um elemento de 125 x 145 x 40 x 20 cm.

Detalhes construtivos

Vamos resolver a seguir um conjunto de detalhes construtivos importantes para a execução da sapata.

Apoio para forma do pilar

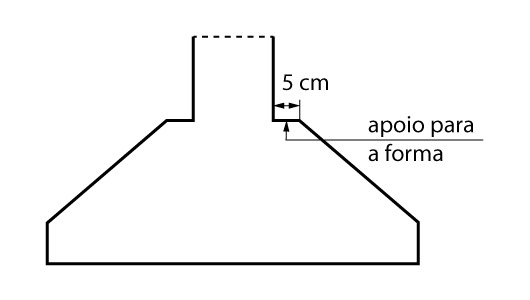
O primeiro detalhe construtivo que vamos aplicar é o diferença entre seção de topo da sapata e a seção do pilar. Tal diferença é recomendada para que exista um apoio para as formas do pilar. Nesse resolução adotaremos um espaço de 5 cm para cada lado do pilar.

Região inclinada das sapatas

Vamos verificar agora se o ângulo da região inclinada da sapata é inferior ao ângulo de talude natural do concreto (\mathrm{\alpha = 30 \deg}), de modo que a concretagem possa ser feita sem a utilização de formas nessa região.

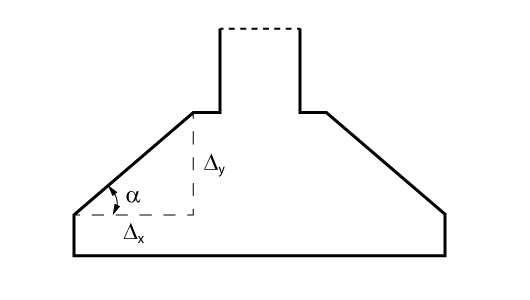
O deslocamento vertical para o cálculo do ângulo é:

\mathrm{\Delta_y = h - h_0 = 40-20}

\mathrm{\Delta_y = 20 \; cm}

Enquanto o deslocamento horizontal é:

\mathrm{\Delta_x = \dfrac{A - a_p}{2} - 5=\dfrac{125 - 20}{2} - 5}

\mathrm{\Delta_x = 47,5 \; cm}

Agora é possível calcular o ângulo da região inclinada da sapata apenas fazendo o arcotangente:

\mathrm{atan \left( \dfrac{\Delta_y}{\Delta_x} \right)}

\mathrm{atan \left( \dfrac{20}{47,5} \right) = 22,8º}

Logo, utilizando as dimensões escolhidas, é possível executar esta sapata sem utilização de formas na região inclinada.

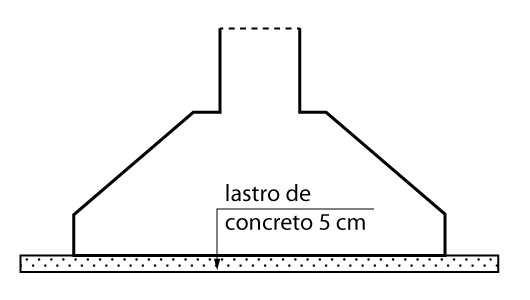
Lastro de concreto sob sapatas

A norma ABNT/NBR: 6122 (2019) exige que a sapata seja concretada sobre um lastro de concreto não estrutural com espessura mínima de 5 cm. Dessa forma, consideraremos a espessura mínima recomendada de 5 cm.

O objetivo desse post foi fixar o conhecimento de dimensionamento geométrico de sapata através de um exemplo aplicado.

Caso queria continuar seus estudos a respeito de sapatas de concreto armado, recomendo agora aprender sobre o dimensionamento da área de aço.

Se você ficou com alguma dúvida sobre o assunto, basta deixar nos comentários abaixo.

---

Fonte:

BASTOS, P. S. S. Sapatas de fundação. 2016 Notas de Aula.

ASSOCIAÇÃO BRASILEIRA DE NORMAS TÉCNICAS. NBR 6122: Projeto e execução de fundações – Procedimento. Rio de Janeiro, 2019.