A partir do momento que você já aprendeu como calcular as dimensões de sapatas submetidas a cargas centradas, o próximo passo será calcular a área de aço necessária para resistir aos esforços de tração.
Nesse post você irá aprender a calcular a área de aço necessária para sapatas submetidas a cargas centradas, ou seja, sem momentos solicitantes.
Método CEB-70 para sapatas
Um método bastante conhecido para o dimensionamento da área de aço de sapatas de concreto armado é o presente na CEB-70.
Condição de aplicação do método
Antes de avançarmos para o método em si, é necessário conhecermos as condição em que é possível aplicar o mesmo.
Conforme proposto pelo CEB-70, para aplicação desta formulação em sapatas, as mesmas devem apresentar a seguinte condição geométrica:
\mathrm{\dfrac{h}{2} \leq c \leq 2 \cdot h }
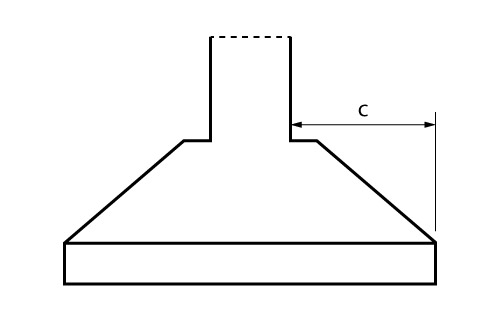
Conceitos do método
Agora sim podemos conferir o entendimento do método para o cálculo de sapatas de concreto armado.
Esse método consiste em analisar a sapata como uma viga em balanço. Dessa forma, essa viga estaria submetida a um carregamento vertical de baixo para cima referente a reação do solo, decorrente dos esforços solicitantes, na sapata.
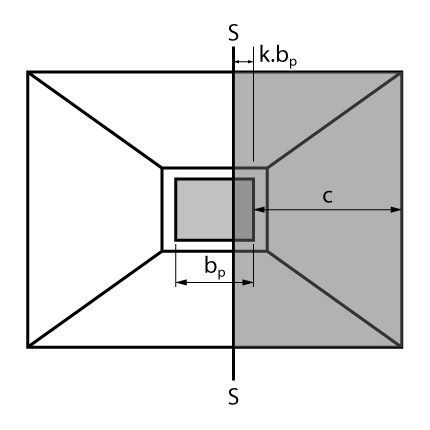
Como apresentado na figura acima, a seção S-S utilizada para dimensionamento passa a uma distância \mathrm{x = c + k \cdot b_p} da face da sapata.
Onde c, vale o balanço (ou aba) da sapata naquela direção e como comentado em publicações anteriores vale:
\mathrm{c = \dfrac{B-b_p}{2}}
O \mathrm{b_p} vale a dimensão do pilar naquela direção e o \mathrm{k} vale o percentual da dimensão do pilar que a seção de dimensionamento irá avançar na direção do pilar.
O valor de \mathrm{k} varia de acordo com a literatura pesquisada, mas comumente utiliza-se \mathrm{k=0,15}. Assim sendo, podemos calcula o comprimento da viga em balanço a partir da equação abaixo:
\mathrm{x = \dfrac{B - b_p}{2} + 0,15 \cdot b_p}
Cálculo da reação do solo
No caso estudado nessa publicação, temos sapatas submetidas a cargas centradas. Assim sendo, a tensão atuante no solo pode ser calculada pela equação abaixo:
\mathrm{\sigma = \dfrac{N}{S_{sap}} }
Essa formulação nos dará a reação do solo por unidade de área, que será utilizada para o dimensionamento da armação.
Para transformar essa reação por área em uma reação por unidade de comprimento, basta que multipliquemos a mesma por uma largura qualquer. Isso ficará mais claro quando formos resolver um sapata mais adiante nesse mesmo post.
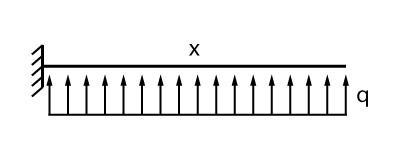
Recomendo multiplicar a reação por área por uma largura de 1,0 m. Uma vez que, com isso teremos uma carregamento linear representando uma largura de 1,0 m da sapata e consequentemente, a área de aço calculada será também obtida para cada metro.
Obtenção do momento solicitante
Agora que já temos o esquema de reação distribuída para a viga em balanço que representa uma seção da sapata, basta calcularmos o momento atuante na mesma (seção S-S).
A força equivalente ao bloco retangular pode ser obtida pela área do retângulo:
\mathrm{ F = q \cdot x }
Já que se trata de um retângulo a posição do ponto de aplicação estará localizada na metade do comprimento do mesmo:
\mathrm{ d = \dfrac{x}{2} }
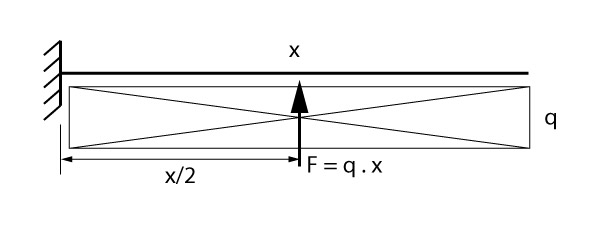
Dessa forma, o momento máximo será calculado pela multiplicação da força equivalente e da distância do ponto de aplicação da mesma:
\mathrm{ M_{máx} = \dfrac{q \cdot x^2}{2} }
Área de aço de sapatas
É possível utilizarmos o mesmo entendimento utilizado para o dimensionamento de vigas para o dimensionamento de sapatas.
Sendo assim, a área de aço necessária será basicamente um momento atuante dividido pelo produto do braço de alavanca e tensão de escoamento do aço utilizado.
\mathrm{ As = \dfrac{M}{Z \cdot f_{yd}} }
Conforme Machado (1985) afirma, para o caso sapata com regiões inclinadas, podemos aproximar o braço de alavanca para \mathrm{z = 0,85 \cdot d}, garantindo um erro máximo de 10%.
Dessa forma, a área de aço pode ser calculada pela seguinte formulação:
\mathrm{ As = \dfrac{M_{Sd}}{0,85 \cdot d \cdot f_{yd}} }
Vale lembrar que como o momento utilizado nessa etapa foi obtido para uma faixa de 1,0 m de largura, a área de aço também equivale a uma faixa de mesma largura.
Armadura mínima para sapatas
Na literatura é possível encontrar algumas proposições para armadura mínima em sapatas.
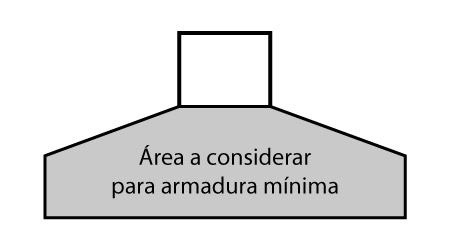
Nessa publicação iremos considerar como armadura mínima como uma taxa da área de concreto da seção levando em consideração a superfície inclinada, conforme ilustra a figura abaixo.
Área para armadura mínima de sapatas
Como se trata de um trapézio somado a um retângulo, esta área pode ser calculada pela seguinte expressão:
\mathrm{ A_c = B \cdot h_0 + \dfrac{B + b_p}{2} \cdot (h - h_0) }
Analisando agora a taxa que multiplica a área de concreto, iremos utilizar o mesmo \mathrm{\rho_{min}} utilizado para vigas de concreto armado.
O valor de \mathrm{\rho_{min}} pode ser obtido na tabela abaixo, fornecida na ABNT/NBR: 6118 (2014), para cada classe de concreto.
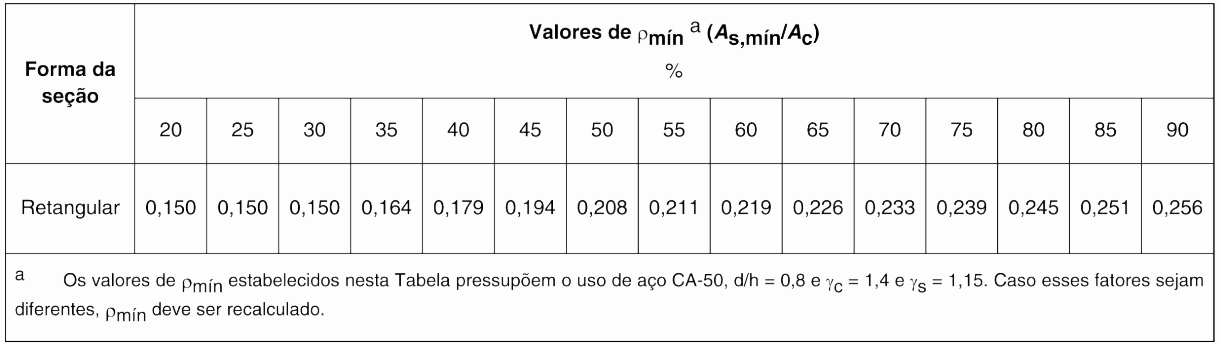
Dessa forma, o cálculo da área de aço mínima será:
\mathrm{As_{min} = \rho_{min} \cdot A_c}
É interessante que ao obtermos essa área também dividirmos a mesma pela largura da seção analisada, a fim de obter também uma área de aço por metro de largura. Com isso, poderemos comparar a mesma com a área de aço calculada.
Exemplo aplicado
A fim de aplicarmos os conhecimentos aprendidos nessa publicação, daremos prosseguimento a uma sapata que já teve suas dimensões dimensionadas em um post anteriore.
Se trata de uma sapata, calculada para um concreto classe C30, que suporta um pilar de 20 x 40 cm e esta submetida a uma carga vertical de 500 kN (valor característico). Nessa resolução, encontramos as seguintes dimensões para solução da sapata: 125 x 145 x 40 x 20.
Verificação da condição da CEB-70
Inicialmente, é necessário verificar se a condição \mathrm{\dfrac{h}{2} \leq c \leq 2 \cdot h } é atendida.
[interesse-fundacoes-rasas]No caso, temos que \mathrm{ c = \dfrac{145-40}{2} = 52,5 \; cm }. Então, uma vez que \mathrm{ h = 40 \; cm }, temos que:
\mathrm{20 \leq 52,5 \leq 80 }
Como \mathrm{c} se encontra dentro do intervalo aceitável, podemos continuar com o método.
Cálculo da reação do solo
No caso, temos uma carga de 500 kN sobre uma área de 125 x 145 cm. Dessa forma, calculando a reação por área no solo:
\mathrm{\sigma = \dfrac{500}{125 \cdot 145}}
\mathrm{\sigma = 0,028 \; kN/cm²}
Para obtermos agora o carregamento que será distribuído linearmente em uma faixa de 1,0 m, basta multiplicarmos por 100 cm.
\mathrm{q = \sigma \cdot 100 \; cm}
\mathrm{q = 2,8 \; kN/cm}
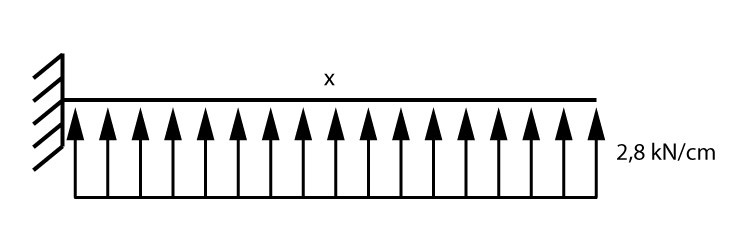
Calculando o momento na seção
Vamos agora calcular o momento que será utilizado para o dimensionamento da armação da sapata.
Um vez que já temos o carregamento distribuído, falta apenas calcular o comprimento da viga equivalente:
\mathrm{x = c + 0,15 \cdot b_p}
Nesse caso, iremos considerar o \mathrm{b_p} como o maior valor entre os dois:
\mathrm{x = \dfrac{145-40}{2} + 0,15 \cdot 40}
\mathrm{x = 58,5 \; cm}
O momento atuante da seção do engastamento então será:
\mathrm{ M_{máx} = \dfrac{q \cdot x^2}{2} }
\mathrm{ M_{máx} = \dfrac{2,8 \cdot 58,5^2}{2} }
Obtemos então o momento característico:
\mathrm{ M_{máx} = 4791 \; kN \cdot cm}
Área de aço da sapata
Em posse agora do momento característico podemos partir para o dimensionamento da área de aço.
Conforme comentado anteriormente, iremos considerar o braço de alavanca igual a \mathrm{ 0,85 \cdot d }.
\mathrm{ As = \dfrac{M_{Sd}}{0,85 \cdot d \cdot f_{yd}} }
Para a altura útil, vamos utilizar \mathrm{ d = h - 5 = 35 \; cm }. Como utilizaremos um aço CA-50, o valor de \mathrm{f_{yd}} será 43,48 kN/cm².
Assim sendo, a área de aço necessária será:
\mathrm{ As = \dfrac{1,4 \cdot 4791}{0,85 \cdot 35 \cdot 43,48} }
\mathrm{ As = 5,19 \; cm^2 }
Vamos lembrar que essa área de aço foi obtida para uma faixa de 1,0 m, ou seja, é necessário colocar 5,19 cm² por metro.
Área de aço mínima
Verificando agora a área de aço mínima, inicialmente vamos calcular a área de aço do conjunto trapézio-retângulo:
\mathrm{ A_c = B \cdot h_0 + \dfrac{B + b_p}{2} \cdot (h - h_0) }
Analisando a seção em que a largura é de 145 cm:
\mathrm{ A_c = 145 \cdot 20 + \dfrac{145 + 40}{2} \cdot (40 - 20) }
\mathrm{ A_c = 4750 \; cm^2 }
Como se trata de um concreto com resistência característica de 30 MPa, utilizaremos \mathrm{\rho_{min} = 0, 15 \%}. Assim sendo, a área de aço mínima será:
\mathrm{As_{min} = \rho_{min} \cdot A_c}
\mathrm{As_{min} = \dfrac{0,15}{100} \cdot 4750 = 7,125 \; cm^2}
Dividindo essa área de aço por 1,45 m, a largura considerado no cálculo da área de concreto, vamos obter a área de aço mínima por metro:
\mathrm{As_{min} = \dfrac{7,125}{1,45} = 4,91 \; cm^2/m}
Como a área de aço mínima é inferior a área de aço calculada, seguiremos a escolha da bilola com a área calculada.
Seleção da armação
Agora que já sabemos que será necessário utilizar uma área de aço de 5,19 cm²/m, vamos utilizar uma tabela que nos forneça a área de aço por metro a partir da bitola e do espaçamento.

Conforme apresentado na tabela acima, podemos propor como solução bitolas de 10.0 mm a cada 15 cm, o que fornece uma área de aço efetiva de 5,33 cm²/m, superior aos 5,19 cm²/m calculados.
Parabéns por ter chegado até aqui! Nesse momento você aprendeu a dimensionar sapatas de concreto armado submetidas a carregamentos centrados. Se você gostou desse texto ou se ainda possui alguma dúvida, deixe uma mensagem nos comentários abaixo!
Fonte:
ARAÚJO, J. M. Curso de Concreto Armado. Rio Grande: Editora Dunas, 2014. v. 4
BASTOS, P. S. S. Sapatas de fundação. 2016 Notas de Aula.
MACHADO, C.P. Edifícios de Concreto Armado – Fundações. São Paulo, FDTE, EPUSP, nov. 1985, p.11.31-11.33.
ASSOCIAÇÃO BRASILEIRA DE NORMAS TÉCNICAS. NBR 6118: Projeto de estruturas de concreto – Procedimento. Rio de Janeiro, 2014.
Gostaria de ter acesso a um curso sobre modelagem de alvenaria estrutural no Revit?
Aproveite enquanto está com um preço especial.

Excelente material.
Muito obrigado, Jovane!
Ótimo o material. Muito bem explicado.
Muito obrigado, Leison!
Parabéns pela forma de explanar o assunto! Não deixa duvidas!
Obrigado, Osmar!
Serviu para poder tirar as minhas duvidas estou grato pelo material, Valeu.
Um abraço.
Abraço!