Fórmula de Manning: condutos retangulares

A fórmula de Manning é muito utilizada para escoamento em superfícies livres.

Você já deve ter ouvido seu professor dizer isso. Ou então já leu essa frase em algum livro de hidráulica.

Mas afinal: o que é escoamento em superfície livre? E o que é a fórmula de Manning?

Se você quer saber as respostas para essas perguntas, você está no lugar certo!

Te prometo, que ao final desse post, você saberá exatamente o que é a fórmula de Manning e quando ela deve ser utilizada.

Agora, vamos logo ao conteúdo!

Lembrando que você pode acompanhar também esse conteúdo através da videoaula que preparamos pra você, vou deixar logo aqui abaixo. Bons estudos!

Escoamento em superfícies livres

Bem, antes de explicarmos a fórmula de Manning, você precisa entender alguns outros conceitos, para melhor saber utilizar tal fórmula.

Um desses conceitos é o de escoamento em superfície livre.

Conduto livre, nada mais é, do que um conduto em que o escoamento no líquido se dá com a pressão atmosférica atuando na superfície do líquido.

Para esse tipo de escoamento o conduto pode ser completamente aberto, como é geralmente o caso de canais, ou podem ser fechados, como em galerias de águas pluviais.

Podemos citar também as calhas de sistemas de águas pluviais, muito comuns no dia-a-dia. São exemplos de condutos livres abertos.

Como o escoamento se dá sob pressão atmosférica, diferentemente de um conduto fechado, em uma superfície livre, o escoamento ocorre necessariamente por gravidade!

Agora que você já sabe o que é um escoamento em superfície livre, vamos tratar um pouco sobre os elementos geométricos para esse tipo de escoamento!

Elementos geométricos

Considere a seção de um conduto livre representado na figura abaixo.

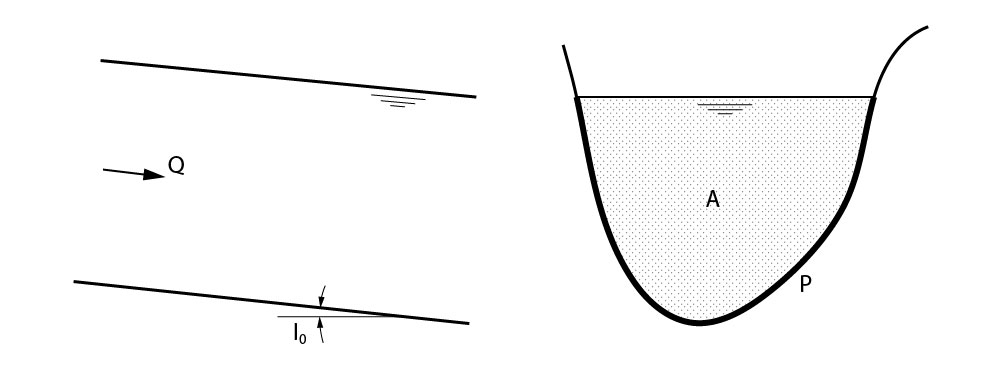
Para essa seção, podemos perceber alguns elementos geométricos importantes para corretos cálculos relacionados a esse conduto.

• Área molhada (A): essa é toda a área da seção reta do escoamento.
• Perímetro molhado (P): é o perímetro de contato entre o conduto e o líquido, considerando fundo e paredes.
• Raio Hidráulico (R_h): é razão entre a área molhada e o perímetro molhado.
• Declividade de fundo (I_o): é a declividade longitudinal do canal. De maneira geral, tais declividades tem valores baixos, sendo da ordem de 1% para calhas de águas pluviais, e valores ainda bem inferiores para canais. Podemos expressar a declividade de fundo como:

Vale ressaltar que existem outros diversos elementos geométricos que são importantes para a total descrição do escoamento livre.

Porém, como vamos falar sobre a fórmula de Manning nesse post, julgo que tais elementos geométricos sejam suficientes para entender e aplicar a formulação.

Melhore seus projetos com o conhecimento aprofundado em instalações pluviais. Nosso curso detalhado cobre tudo, desde o planejamento até a execução. Descubra mais e inscreva-se hoje mesmo!

Então, agora que você já conhece os elementos geométricos necessários, vamos estudar a fórmula de Manning.

Fórmula de Manning

A fórmula de Manning foi proposta em 1889 e, atualmente, é uma das mais utilizadas para o cálculo de escoamentos em superfícies livres.

Tal formulação nada mais é do que resultado de vários experimentos para a correlação do coeficiente C de Chézy com o raio hidráulico (R_h) da seção. Manning tal relação:

\mathrm{C=\dfrac{R_{h}^{1/6}}{n}}

Onde:

• C: coeficiente da formulação de Chézy, que varia com o fator de atrito das paredes do conduto.
• n: coeficiente que não possui significado físico determinado e que também não é adimensional, mas que varia principalmente com o material do conduto (ou canal).

Vale ressaltar que tal consideração de Manning é válida para escoamentos permanentes, uniformes e turbulentos rugosos, com elevado número de Reynolds.

Pois bem, de posse dessa relação apresentada, Manning reajustou fórmulas e chegou a seguinte formulação, a famosa fórmula de Manning.

\mathrm{\dfrac{n\cdot Q}{\sqrt{I_0}}=A\cdot R_{h}^{2/3}}

Onde:

• Q: vazão de escoamento.

Para não termos problemas com unidades, aconselho utilizar sempre o SI, ou seja:

• A em m²;
• R_h em m;
• Q em m³/s.

A seguir, apresentarei algumas tabelas retiradas do livro Hidráulica Básica do Prof. Porto, com valores usuais para o coeficiente n.

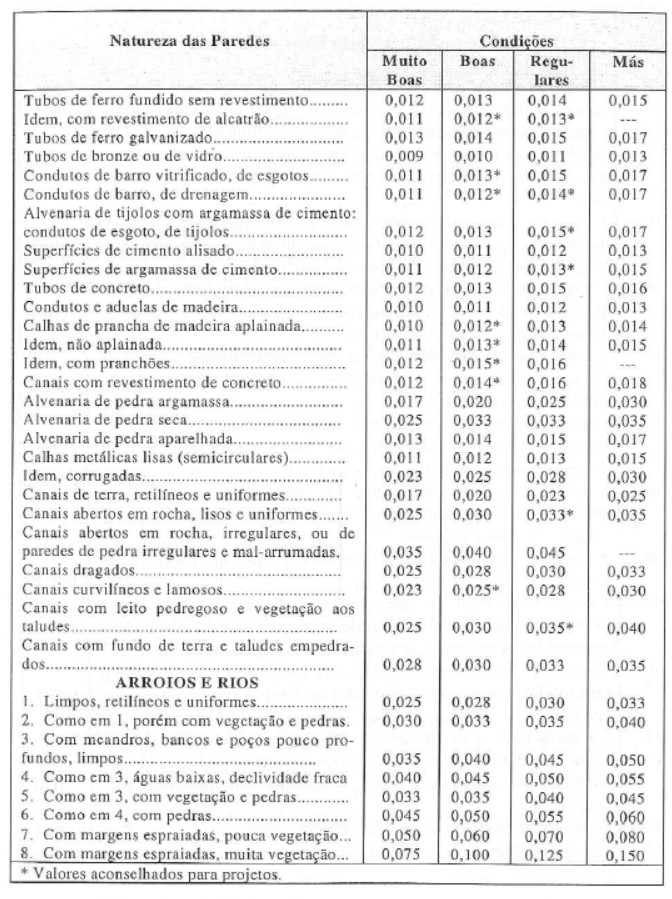
Agora que você já conhece a fórmula de Manning e suas aplicações, vamos resolver juntos um exemplo prático?

Fórmula de Manning – exemplo proposto

Então, tomemos como exemplo, uma situação prática do dia-a-dia, que é uma calha de telhado, do sistema de águas pluviais.

Considere a seguinte calha retangular, de material PVC, apresentada na figura abaixo.

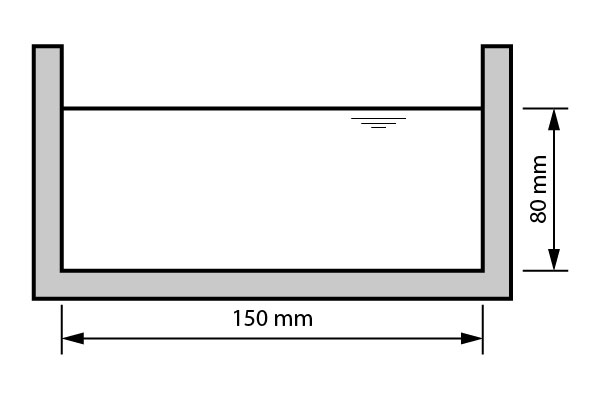
Sabendo que a inclinação longitudinal da calha é de 1%, qual o valor máximo de vazão que pode escoar por essa calha, mantendo o nível d’água apresentado na figura?

Resolução

Então, o primeiro passo para a utilização da fórmula de Manning é o cálculo dos elementos geométricos da seção.

Cálculo de A

A área molhada engloba toda a área de seção transversal do escoamento, apresentado na figura.

Logo, por se tratar de um retângulo, a resolução é bem simples:

\mathrm{A=b\cdot h=0,15m\cdot 0,08m}

\mathrm{A=0,012 m^2}

Cálculo do raio hidráulico

Para o cálculo do raio hidráulico, devemos antes calcular o perímetro molhado.

Para esse cálculo, devemos lembrar que a “face superior” do escoamento não deve ser considerada, pois não está em contato com a parede da tubulação.

Logo, temos que o perímetro hidráulico do nosso exemplo vale:

\mathrm{P=0,15m+0,08m+0,08m}

\mathrm{P=0,31m}

Logo, o raio hidráulico é:

\mathrm{R_h=\dfrac{A}{P}= \dfrac{0,012}{0,31} }

\mathrm{R_h=0,0387m}

Valor de n

Para a aa adoção do valor do coeficiente n, não podemos utilizar as tabelas apresentadas durante o texto, visto que o material da calha (PVC) não é abordado na tabela.

Porém, podemos utilizar uma pequena tabela contida na NBR 108444, que é a norma referente a instalações de águas pluviais. Segue a tabela.

Material	n
Plástico, fibrocimento, aço, metais não-ferrosos	0,011
Ferro fundido, concreto alisado, alvenaria revestida	0,012
Cerâmica, concreto não-alisado	0,013
Alvenaria de tijolos não-revestida	0,015

Logo, utilizaremos n=0,011.

Fórmula de Manning

Agora que já sabemos todos os elementos geométricos necessários, podemos utilizar a fórmula de Manning.

\mathrm{\dfrac{n\cdot Q}{\sqrt{I_0}}=A\cdot R_{h}^{2/3}}

\mathrm{\dfrac{0,011\cdot Q}{\sqrt{0,01}}=0,012\cdot 0,0387^{2/3}}

Resolvendo essa equação, chegamos ao seguinte resultado:\mathrm{Q=0,01248 m^3/s}

Pronto, determinamos através da fórmula de Manning que a capacidade de vazão da calha em questão é de 0,01248 m³/s, ou 12,48 l/s.

Planilha de resolução

Outra forma de resolver o mesmo exemplo apresentado é através da nossa planilha de dimensionamento de elementos de águas pluviais.

Obviamente, a planilha é bem mais completa para a aba de calhas, contendo os valores pluviométricos de cada região para determinados tempos de retorno, além do possível cálculo de calhas semicirculares.

Mas bem, vamos à resolução. Como nosso exemplo é simples, basta inserir na planilha:

• Geometria da calha: retangular;
• Base da calha: 150 mm;
• Altura da lâmina d’água: 80 mm;
• Inclinação da calha: 1%;
• Rugosidade do material da calha (n): 0,011.

Com esses dados de entrada, a planilha nos retorna a capacidade da calha, em l/min, conforme apresentado na figura abaixo!

Viu como não foi tão difícil entender e utilizarmos a fórmula de Manning?

Espero que esse post tenha te ajudado, mas caso você ainda tenha alguma dúvida, pode deixar nos comentários que vai ser um prazer responder.

Além disso, se tiver alguma alguma sugestão para posts futuros, comenta aqui embaixo que a gente vai fazer o máximo para poder atender!

Não deixe de seguir nosso blog, assinar nossa newsletter, além de acompanhar nosso canal no Youtube e ficar por dentro das novidades!

Até a próxima!