No nosso post anterior sobre Curva Horizontal com Transição, explicamos o que e como devemos calcular alguns dos principais seus elementos. Portanto, se você ainda não leu esse post, recomendamos que dê uma rápida olhada antes de começarmos.
Agora, vamos solidificar o que foi aprendido sobre as Curvas Horizontais até o momento. Para tanto, propomos um exemplo prático bem simples. Confira abaixo!
Exemplo prático
Você é responsável por um projeto rodoviário e necessita determinar os elementos de uma curva de concordância horizontal com transição em espiral de raio conservado, sabendo que o estaqueamento da estrada é feito a cada 20 m, o ponto de interseção está localizado na estaca 228+17 m, o ângulo de deflexão das tangentes é 35°, o raio da curva circular mede 500 m e sua velocidade diretriz é 80 km/h.
RESOLUÇÃO:
Passo 01: Verificar a necessidade da transição
O primeiro passo para resolvermos esse exemplo é verificar se, de fato, será necessário utilizarmos a curva de transição para realizar a concordância da curva horizontal. Para isso, faremos uso da tabela abaixo:
Tabela 1 – Valores limite de raio para a dispensa de curvas de transição

Como nosso raio é 500 m e a velocidade diretriz da pista é 80 km/h, podemos confirmar a necessidade da transição.
Passo 02: Calcular o comprimento do trecho em espiral
Como necessitamos realizar a concordância da curva, iremos agora descobrir o valor recomendado para o comprimento do trecho de transição em espiral.
Para isso, devemos seguir alguns critérios, apresentados a seguir.
Critério de segurança
Esse primeiro critério estabelece o menor valor permitido para o comprimento da transição e é calculado conforme abaixo, lembrando que esse valor não pode ser inferior a 30 m.
\mathrm{le_{mín}=\dfrac{V}{1,8}=\dfrac{80}{1,8}=44,44\:m}
Critério dinâmico de Barnett
O segundo critério estabelece uma taxa máxima de variação da aceleração centrífuga, com o objetivo de minimizar os efeitos negativos do surgimento brusco dessa força e é calculado conforme abaixo.
\mathrm{le_{mín}=0,036\cdot\dfrac{V^3}{R}=0,036\cdot\dfrac{80^3}{500}}
\mathrm{le_{mín}=36,86\:m}
Comprimento máximo
O comprimento máximo da transição será o correspondente ao ângulo central nulo da curva circular e é calculado conforme abaixo, lembrando que o ângulo será expresso em radianos.
\mathrm{le_{máx}=R.AC=500.0,61=305,43\:m}
Comprimento a ser adotado
Por fim, o comprimento que deverá ser adotado para o comprimento do ramo da espiral será a média entre o máximo e mínimo encontrados pelos critérios anteriores, lembrando que o valor resultante deverá ser arredondado para um valor igual a um número inteiro de estacas, ou múltiplo de 10.
\mathrm{le_{adot}=\dfrac{le_{mín}+le_{máx}}{2}=\dfrac{44,44+305,43}{2}}
\mathrm{le_{adot}=174,94\:m}
\mathrm{le_{adot}=\mathbf{170\:m}}
Passo 03: Cálculo do ângulo central do trecho em espiral
Os dois ângulos da espiral (Φ) são aqueles que, somados com o ângulo central do trecho circular, resulta no ângulo de deflexão das tangentes externas e são obtidos por:
\mathrm{Φ=\dfrac{le}{2.R}=\dfrac{170}{2.500}=0,17\:rad}
\mathrm{Φ=\mathbf{9º44'25"}}
Passo 04: Cálculo do ângulo central do trecho circular
O ângulo circular (θ) nada mais é do que o ângulo formado entre os pontos SC e CS da curva e é obtido por:
\mathrm{θ=AC-2.Φ=35º-2.(9º44'25")}
\mathrm{θ=\mathbf{15º31'10"}}
Passo 05: Cálculo do desenvolvimento circular
Desenvolvimento da curva (Dθ), neste caso, representa o comprimento do arco que vai desde o SC a CS e é obtido pela seguinte expressão, lembrando que o ângulo será dado em radianos:
\mathrm{D_θ=R.θ=500.0,27=\mathbf{135,43\:m}}
Passo 06: Cálculo das coordenadas do ponto SC em relação a TS
\mathrm{Xc=\dfrac{le.Φ}{3}\cdot\left(1-\dfrac{Φ^2}{14}+\dfrac{Φ^4}{440}\right)} \mathrm{Xc=\dfrac{170.0,17}{3}\cdot\left(1-\dfrac{0,17^2}{14}+\dfrac{0,17^4}{440}\right)}
\mathrm{Xc=\mathbf{9,61\:m}}
\mathrm{Yc=le\left(1-\dfrac{Φ^2}{10}+\dfrac{Φ^4}{216}\right)} \mathrm{Yc=170\left(1-\dfrac{0,17^2}{10}+\dfrac{0,17^4}{216}\right)}
\mathrm{Yc=\mathbf{169,51\:m}}
Passo 07: Cálculo das coordenadas do ponto PC’ em relação a TS
Esse passo é extremamente importante para o cálculo da tangente externa da curva com transição.
\mathrm{p=Xc-R.[1-cos(Φ)]}
\mathrm{p=9,61-500.[1-cos(9º44'25")]}
\mathrm{p=\mathbf{2,40\:m}}
\mathrm{q=Yc-R.sen(Φ)}
\mathrm{q=169,51-500.sen(9º44'25")}
\mathrm{q=\mathbf{84,92\:m}}
Passo 08: Cálculo do deslocamento da curva circular
Deslocamento (t) é o valor do deslocamento do centro da curva circular para a realização da transição espiral entre a curva circular e a o trecho reto da estrada e é obtido por:
\mathrm{t=\dfrac{p}{cos(AC/2)}=\dfrac{2,40}{cos(35º/2)}=\mathbf{2,52\:m}}
Passo 09: Cálculo da tangente externa da curva com transição
Tangente externa (TT), neste caso, representa os segmentos de reta que vão do TS ao PI ou do PI ao ST. TT é, então, calculado por:
\mathrm{TT=q+[(R+p)\cdot{tg(AC/2)]}}
\mathrm{TT=84,92+[(500+2,40)\cdot{tg(35/2)]}}
{\mathrm{TT=\mathbf{243,33\:m}}}
Passo 10: Locação dos pontos notáveis TS, SC, CS e ST
Agora que já calculamos todos os elementos necessários, já podemos iniciar a locação da nossa curva, a começar pelos pontos notáveis TS, SC, CS e ST, conforme abaixo:
\mathrm{TS=PI-TT=(228+17\:m)-243,33\:m}
\mathrm{TS=228-226,33\:m=216+240\:m-226,33\:m}
\mathrm{TS=\mathbf{216+13,67\:m}}
\mathrm{SC=TS+le=(216+13,67\:m)+170\:m}
\mathrm{SC=216+183,67\:m=216+9+3,67\:m}
\mathrm{SC=\mathbf{225+3,67\:m}}
\mathrm{CS=SC+D_{θ}=(225+3,67\:m)+135,43\:m}
\mathrm{CS=225+139,10\:m=225+6+19,10\:m}
\mathrm{CS=\mathbf{231+19,10\:m}}
\mathrm{ST=CS+le=(231+19,10\:m)+170\:m}
\mathrm{ST=231+189,10\:m=231+9+9,10\:m}
\mathrm{ST=\mathbf{240+9,10\:m}}
Passo 10: Locação da curva horizontal com transição
O próximo e último passo desse nosso exercício será alocar todas as estacas da curva horizontal, considerandos os dois trechos de transição e o trecho central circular.
Primeiro ramo de transição em espiral
Antes de iniciarmos a locação da primeira espiral, devemos considerar que a locação desse trecho deverá obedecer ao seguinte critério:
- le ≤ 60 m, locar estacas a cada 5 metros;
- Ɩe > 60 m, locar estacas a cada 10 metros.
Portanto, como o le calculado no passo 02 é maior que 60 m, a locação da espiral ocorrerá a cada 10 m, ou seja, deverá haver sempre uma estaca intermediária entre duas estacas inteiras.
Deflexão total do primeiro trecho em espiral
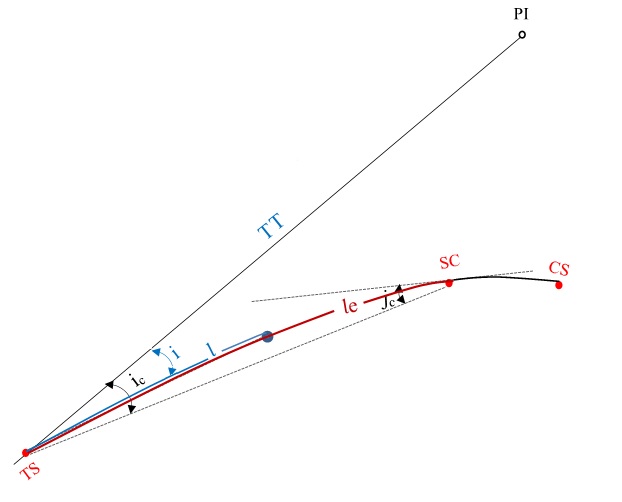
Primeiramente, calcularemos a deflexão acumulada entre os pontos TS E SC, de acordo com a formulação abaixo:
\mathrm{ic=arctg\left(\dfrac{Xc}{Yc}\right)=arctg\left(\dfrac{9,61}{169,51}\right)}
\mathrm{ic=3º\:14'\:41,23"}
Deflexão parcial em função do comprimento da espiral
Após o cálculo da deflexão total do primeiro ramo da espiral, seguiremos para o preenchimento da caderneta de anotação e locação das demais estacas do trecho espiral, utilizando a expressão abaixo:
\mathrm{i_l=ic\cdot\left(\dfrac{l}{le}\right)^2}
Tabela 2 – Caderneta de locação do primeiro trecho espiral
| Estaca | l (m) | ….Deflexão…. | |
| Interia | Fracionária | ||
| TS – 216 | 13,67 m | 0 m | 00º 00′ 00″ |
| 217 | 3,67 m | 10 m | 00º 00′ 40,42″ |
| 217 | 13,67 m | 20 m | 00º 02′ 41,68″ |
| 218 | 3,67 m | 30 m | 00º 06′ 03,78″ |
| 218 | 13,67 m | 40 m | 00º 10′ 46,71″ |
| 219 | 3,67 m | 50 m | 00º 16′ 50,49″ |
| 219 | 13,67 m | 60 m | 00º 24′ 15,10″ |
| 220 | 3,67 m | 70 m | 00º 33′ 00,56″ |
| 220 | 13,67 m | 80 m | 00º 43′ 06,85″ |
| 221 | 3,67 m | 90 m | 00º 54′ 33,98″ |
| 221 | 13,67 m | 100 m | 01º 07′ 21,96″ |
| 222 | 3,67 m | 110 m | 01º 21′ 30,77″ |
| 222 | 13,67 m | 120 m | 01º 37′ 00,42″ |
| 223 | 3,67 m | 130 m | 01º 53′ 50,90″ |
| 223 | 13,67 m | 140 m | 02º 12′ 02,23″ |
| 224 | 3,67 m | 150 m | 02º 31′ 34,40″ |
| 224 | 13,67 m | 160 m | 02º 52′ 27,40″ |
| SC – 225 | 3,67 m | 170 m | 03º 14′ 41,25″ |
A deflexão acumulada em ST equivale ao valor de ic.
[ebook-projetos-rodoviarios]Trecho circular central
Os passos para a locação do trecho circular já foram explicados no post sobre Curvas Horizontais Simples. Caso queira entender esse tópico mais a fundo, é só clicar aqui.
Tabela 2 – Comprimento da corda em função do raio
| Raio (m) | Corda máxima (m) |
| R<150 | 5 |
| 150≤R<300 | 10 |
| R≥300 | 20 |
Conforme a tabela acima, o estaqueamento da curva circular de R=500 m pode ser feito a cada 20 m, não necessitando, portanto, de estacas intermediárias.
Grau da curva circular
\mathrm{Gc=2.arcsen\left(\dfrac{c}{2.R}\right)}
\mathrm{Gc=2.arcsen\left(\dfrac{20}{2.500}\right)=2º\:17'\:31,14"}
Deflexão por metro
\mathrm{d_m=\dfrac{Gc}{2.c}}
\mathrm{d_m=\dfrac{2º\:17'\:31,14"}{2.20}=0º\:03'\:26,28"/m}
Deflexões parciais
Para esse passo, precisamos encontrar a deflexão parcial para 3 cordas importantes: a corda de 16,33 m entre SC e a estaca 226, a corda de 20 m entras as estacas intermediárias e a corda de 19,10 m (10-7,44) entre a estaca 231 e CS.
- Deflexão parcial para a corda de 16,33 m
\mathrm{d_i=d_m.c_i}
\mathrm{d_{16,33}=(0º\:03'\:26,28"/m).16,33=0º\:56'\:08,53"}
- Deflexão parcial para a corda de 20 m
\mathrm{d_i=d_m.c_i}
\mathrm{d_{20}=(0º\:03'\:26,28"/m).20=01º\:08'\:45,60"}
- Deflexão parcial para a corda de 19,10 m
\mathrm{d_i=d_m.c_i}
\mathrm{d_{16,33}=(0º\:03'\:26,28"/m).19,10=01º\:05'\:39,92"}
Após o cálculo da deflexão parcial, seguiremos para o preenchimento da caderneta de anotação e locação das demais estacas, conforme abaixo:
Tabela 3 – Caderneta de locação do trecho circular
| Estaca | Deflexão | ||
| Inteira | Fracionária | Parcial | Acumulada |
| SC – 225 | 3,67 m | 00º 00′ 00″ | 00º 00′ 00″ |
| 226 | 00º 56′ 08,53″ | 00º 56′ 08,53″ | |
| 227 | 01º 08′ 45,60″ | 02º 04′ 54,13″ | |
| 228 | 01º 08′ 45,60″ | 03º 13′ 39,73″ | |
| 228 | 01º 08′ 45,60″ | 04º 22′ 25,33″ | |
| 230 | 01º 08′ 45,60″ | 05º 31′ 10,93″ | |
| 231 | 01º 08′ 45,60″ | 06º 39′ 56,53″ | |
| CS – 231 | 19,10 m | 01º 05′ 39,92″ | 07º 45′ 36,45″ |
A deflexão acumulada entre SC e CS equivale à metade do ângulo central do trecho circular (θ). No nosso resultado, houve apenas uma pequena diferença de 2,9″ em virtude das aproximações.
Segundo ramo de transição em espiral
Assim como no primeiro ramo, o estaqueamento da espiral deverá ocorrer a cada 10 m, com a diferença de que, agora, o sentido da espiral será invertido, ou seja, será feito do fim para o início.
Deflexão total do segundo trecho em espiral
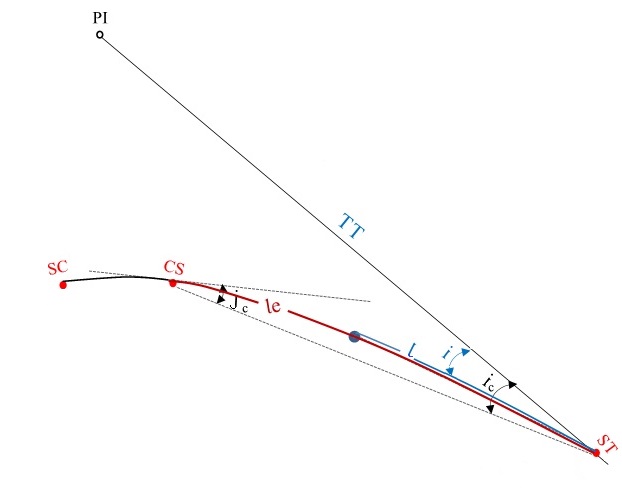
Calcularemos a deflexão acumulada entre os pontos CS e ST, de acordo com a formulação abaixo:
\mathrm{jc=Φ-ic=09º44'25"-03º14'41,25"}
\mathrm{jc=06º\:29'\:43,75"}
Deflexão parcial em função do comprimento da espiral
Após o cálculo da deflexão total do primeiro ramo da espiral, seguiremos para o preenchimento da caderneta de anotação e locação das demais estacas do trecho espiral, utilizando a expressão abaixo:
\mathrm{j_l=\dfrac{90º.(le-l)}{π.R}-ic\cdot\left(\dfrac{le - l}{le}\right)^2}
Tabela 4 – Caderneta de locação do segundo trecho espiral
| Estaca | l (m) | ….Deflexão…. | |
| Interia | Fracionária | ||
| CS – 231 | 19,10 m | 170 m | 00º 00′ 00″ |
| 232 | 9,10 m | 160 m | 00º 33′ 42,23″ |
| 232 | 19,10 m | 150 m | 01º 06′ 03,62″ |
| 233 | 9,10 m | 140 m | 01º 37′ 04,17″ |
| 233 | 19,10 m | 130 m | 02º 06′ 43,88″ |
| 234 | 9,10 m | 120 m | 02º 35′ 02,75″ |
| 234 | 19,10 m | 110 m | 03º 02′ 00,78″ |
| 235 | 9,10 m | 100 m | 03º 27′ 37,98″ |
| 235 | 19,10 m | 90 m | 03º 51′ 54,33″ |
| 236 | 9,10 m | 80 m | 04º 14′ 49,85″ |
| 236 | 19,10 m | 70 m | 04º 36′ 24,53″ |
| 237 | 9,10 m | 60 m | 04º 56′ 38,36″ |
| 237 | 19,10 m | 50 m | 05º 15′ 31,36″ |
| 238 | 9,10 m | 40 m | 05º 33′ 03,52″ |
| 238 | 19,10 m | 30 m | 05º 49′ 14,84″ |
| 239 | 9,10 m | 20 m | 06º 04′ 05,32″ |
| 239 | 19,10 m | 10 m | 06º 17′ 34,96″ |
| ST – 240 | 9,10 m | 0 m | 06º 29′ 43,77″ |
A deflexão acumulada em ST equivale ao valor de jc, com uma pequena diferença de 0,02″ em virtude das aproximações.
Resultado final
O resultado final do nosso estaqueamento da curva horizontal com transição é o seguinte:
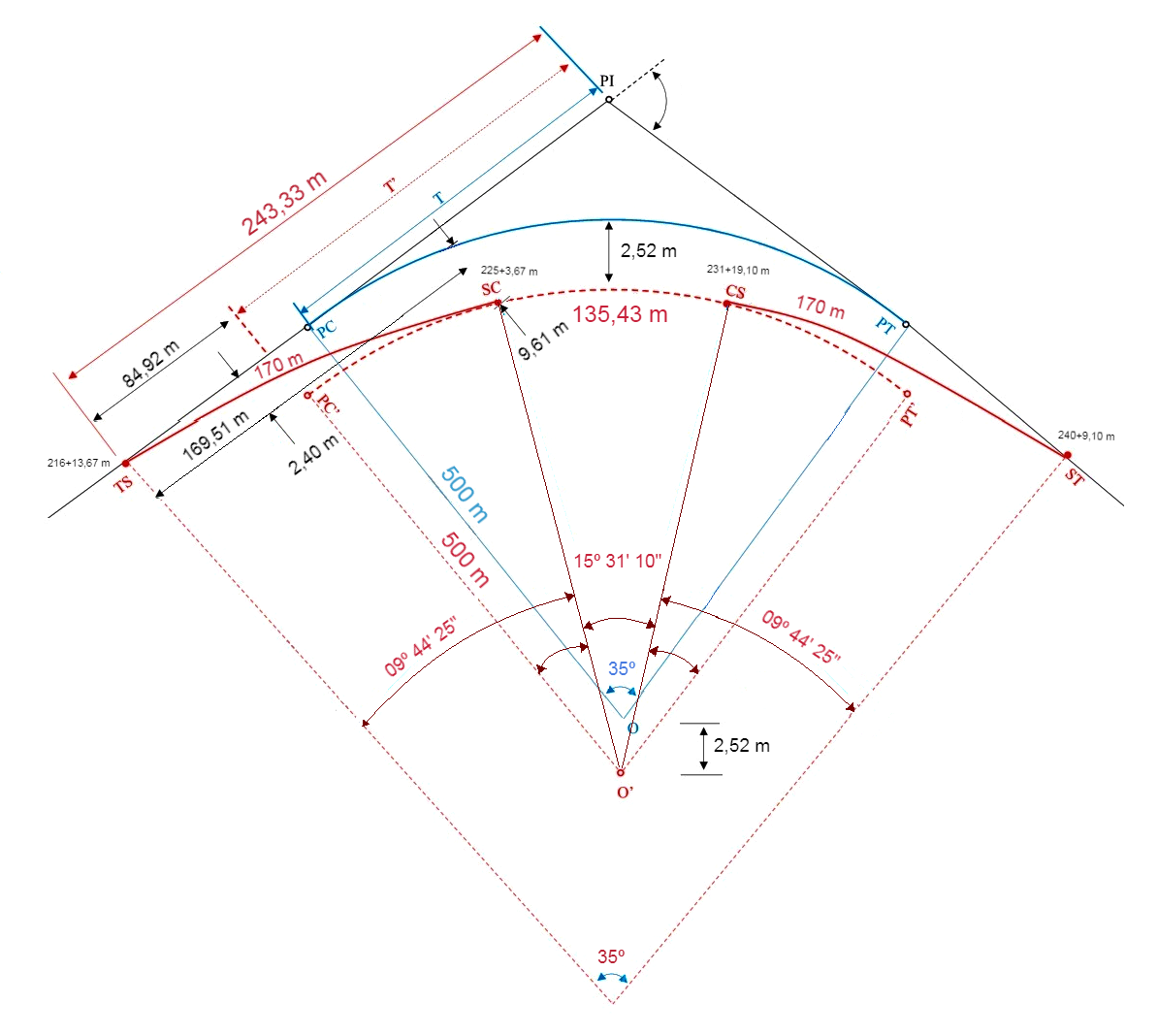
Pois bem pessoal, essas foram algumas considerações a respeito da locação de uma curva horizontal com transição, mas não para por aqui!
Confira agora o super e-Book GRATUITO sobre Projeto Rodoviário que preparamos pra você.
[ebook-projetos-rodoviarios]É claro, no entanto, que esse universo é muito mais amplo do que conseguimos abordar em um e-Book.
Então, se você quiser se aprofundar mais nessa área, sugiro que conheça o curso online Formação em Estradas de um dos nosso parceiros, o Grupo HCT, que é um centro de aperfeiçoamento profissional atuante na área tecnológica desde 1997.
Dito isso, ficamos por aqui e se gostou, não deixa de seguir a gente no Instagram e também no Youtube para receber todas as novidades.

Engenheira Civil pela Universidade Federal do Piauí, engenheira de obra, perita judicial e pós-graduanda em Avaliação, Auditoria e Perícias de Engenharia.
