Você está dirigindo em um trecho reto de uma estrada e, de repente, surge uma curva extremamente fechada, que você não pôde ver antes devido à baixa visibilidade causada pela densa vegetação.
Para essa situação extremamente comum, você tem duas saídas: controlar a velocidade e conseguir realizar a curva de maneira segura ou sair pela tangente e cair no precipício, que você também não viu por causa da vegetação.
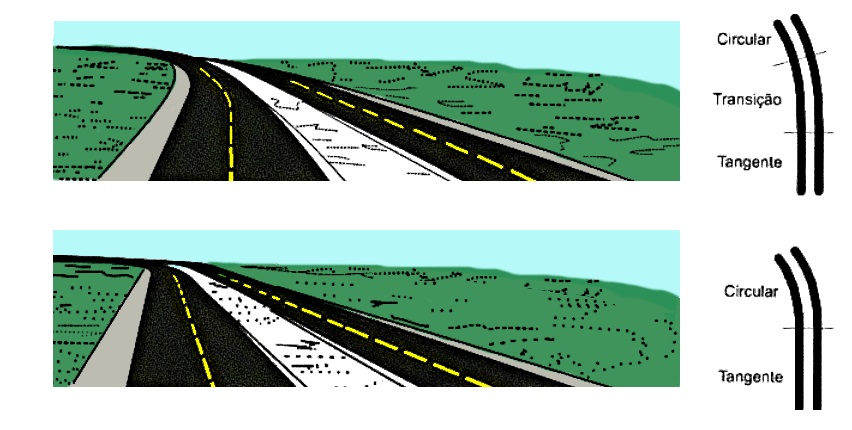
A boa notícia é que a curva é de transição, então você consegue se livrar dessa.
Essa pequena história foi apenas para ilustrar uma situação extremamente corriqueira e também muito perigosa nas estradas.
Um veículo que trafega em um trecho reto não está sujeito a esforços laterais, diferentemente do que ocorre quando ele entra em um trecho curvo. Nessa situação, a força centrífuga começa a atuar, tendendo a desviar o veículo do trajeto e isso ocorre pela brusca mudança de um raio infinito para um raio finito.
E é por isso que sugiram as curvas de transição, pois elas possibilitam uma mudança gradativa de um trecho reto para uma curva circular e, consequentemente, proporcionam um crescimento gradual da aceleração centrífuga.
Dessa foram, as curvas horizontais com transição ajudam a garantir maior segurança aos usuários e a evitar graves acidentes.
Agora, para facilitar nosso entendimento, observe na imagem abaixo a diferença entre uma curva horizontal com transição e uma curva horizontal simples.
Pois bem, sem mais enrolação, nesse post, iremos estudar as curvas horizontais com transição.
Vale lembrar que as curvas horizontais simples já foram abordadas em um post anterior e você pode encontrá-lo clicando aqui. Agora, vamos lá!
E ainda tem mais! Se, ao invés de fazer essa leitura, você preferir assistir uma pequena videoaula minha sobre esse mesmo assunto, basta clicar aqui embaixo!
Quando não usar curva de transição
A primeira coisa que precisamos saber para iniciarmos nosso estudo é que as curvas de transição podem ser dispensadas e, em vez disso, serem usadas as curvas simples.
Para que isso aconteça, o raio da curva circular deve exceder os valores apresentados na tabela a seguir, de acordo com a velocidade diretriz da estrada.
Tabela 1 – Valores limite de raio para a dispensa de curvas de transição
No entanto, se o raio da sua curva for inferior a esses valores, devemos fazer o uso das curvas de transição, que podem ser de vários tipos, como veremos a seguir.
Tipos de curva de transição
Lemniscata de Bernoulli
A Lemniscata de Bernoulli é a curva algébrica do quarto grau de equação cartesiana que se assemelha muito ai símbolo do infinito e sua principal propriedade como curva de transição deve-se ao fato de que a magnitude da curvatura em qualquer ponto é proporcional à distância daquele ponto da origem.
Vejamos:
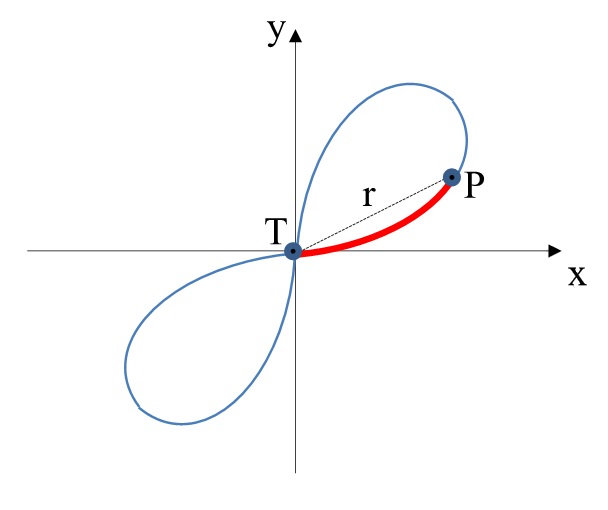
\mathrm{ρ=k/r}
Onde:
- ρ é o raio de curvatura em um ponto P;
- k é uma constante;
- r é o raio vetor.
Parábola cúbica
A parábola cúbica é uma curva gráfica resultantes de uma equação do tipo y=ax³+bx²+c.
Além da sua função matemática muito conhecida, é também utilizada em projetos rodoviários como curva de transição de acordo do a formulação:
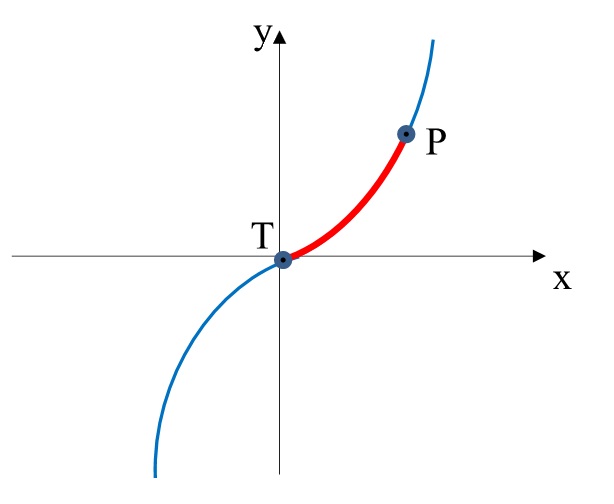
\mathrm{y=\dfrac{x^3}{6.k}}
Onde:
- y é a ordenada do ponto P;
- x é a abcissa do ponto P;
- k é uma constante.
Uma característica importante desse tipo de curva é que as parábolas cúbicas convergem mais lentamente que as espirais e, embora sejam menos precisas que estas, são fáceis de locar em campo por serem expressadas em coordenadas cartesianas.
Espiral de Cornu
A espiral de Cornu, também conhecida como clotóide, é um tipo de curva em que o raio de curvatura é inversamente proporcional ao comprimento, partindo da origem do eixo, conforme a equação abaixo:
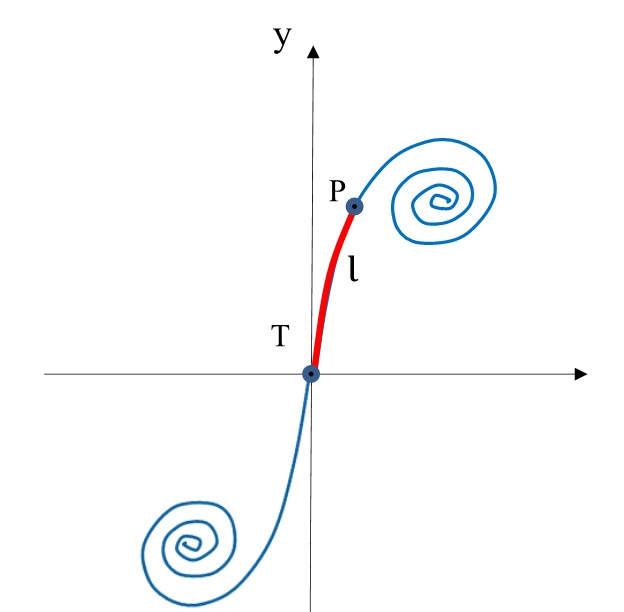
\mathrm{ρ=k/l}
Onde:
- ρ é o raio de curvatura em um ponto P;
- k é uma constante;
- l é o comprimento do ramo da espiral.
Justamente em razão disso, a espiral de Cornu garante um decrescimento linear da curvatura conforme é percorrida, proporcionando, assim, uma variação gradual da força centrífuga.
Com isso, torna-se o tipo ideal de curva de transição, sendo, portanto, recomendada pelo Departamento Nacional de Infraestrutura de Transportes do Brasil.
Tipos de transição em espiral
Como já vimos anteriormente que o tipo de curva de transição mais indicado para as estradas brasileiras é a espiral de Cornu. Portanto, agora iremos estudar os três tipos clássicos de transição usando essa espiral.
Transição de centro e raio conservados
Nesse tipo de transição, basicamente o centro e o raio da curva circular (azul) não são alterados, mantendo a curva no local original, porém as tangentes são afastadas para permitir a inserção dos ramos em espiral (vermelho), conforme o esquema abaixo.
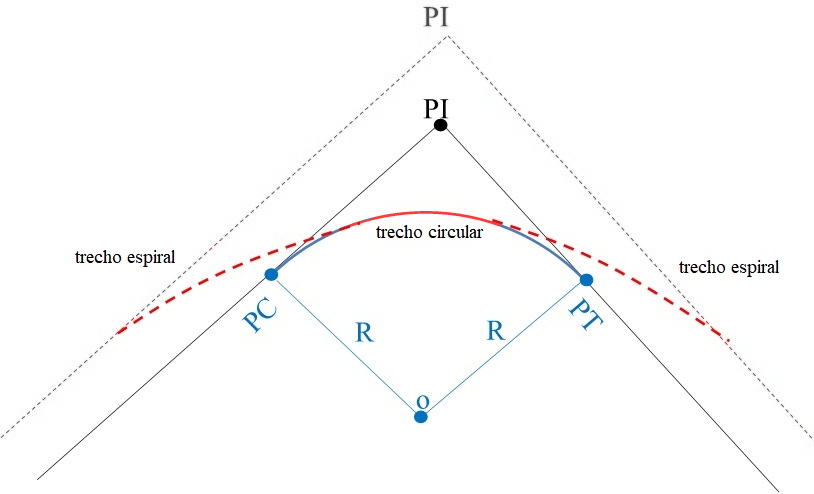
Curva espiral de centro conservado
Para esse segundo tipo de transição, apenas o centro da curva circular é conservado. Nesse caso, o seu raio original (azul) diminui com o objetivo de permitir a inserção dos ramos de transição em espiral (vermelho), conforme a imagem abaixo.
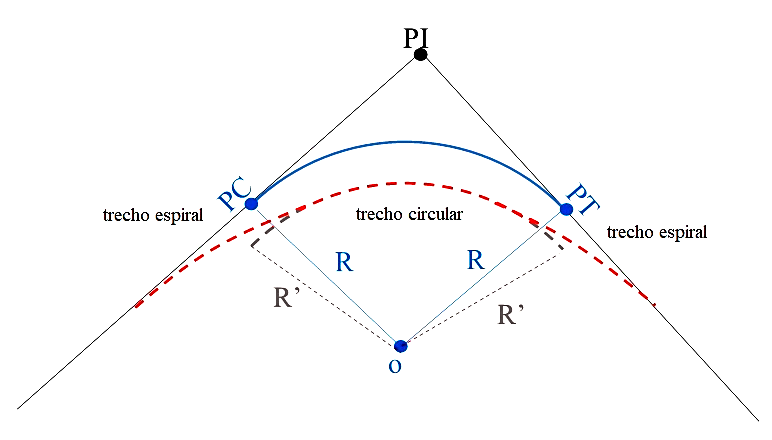
Curva espiral de raio conservado
Por fim, para o último tipo de transição, raio da curva circular é conservado e o centro (o) é deslocado para permitir a inserção dos ramos de transição em espiral (vermelho), conforme abaixo.
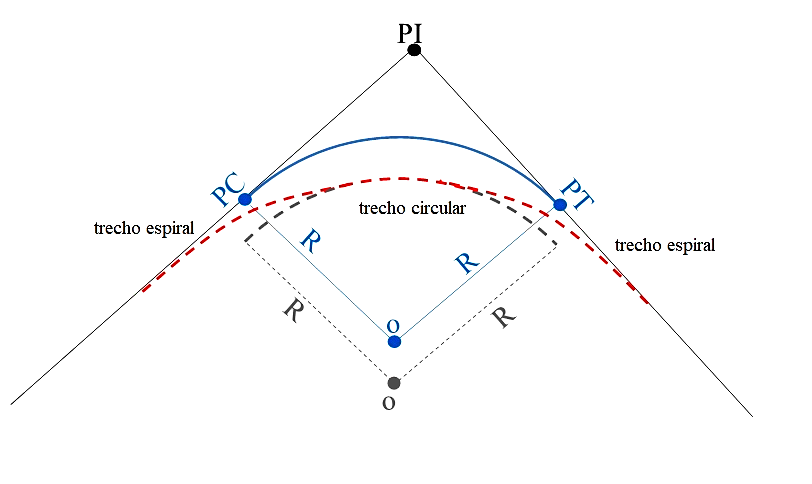
Além disso, esse é o método de transição mais utilizado na construção de rodovias, principalmente para curvas de raio de até 600 m, em virtude da facilidade em deslocar apenas o centro da curva circular.
[ebook-projetos-rodoviarios]Elementos da curva horizontal com transição
Iremos agora conhecer os elementos componentes da curva horizontal com transição e, para ilustrar, usaremos uma curva horizontal clássica com transição em espiral de raio conservado, que é o tipo mais usado.
Ah, para dar zoom na imagem, é só clicar nela.
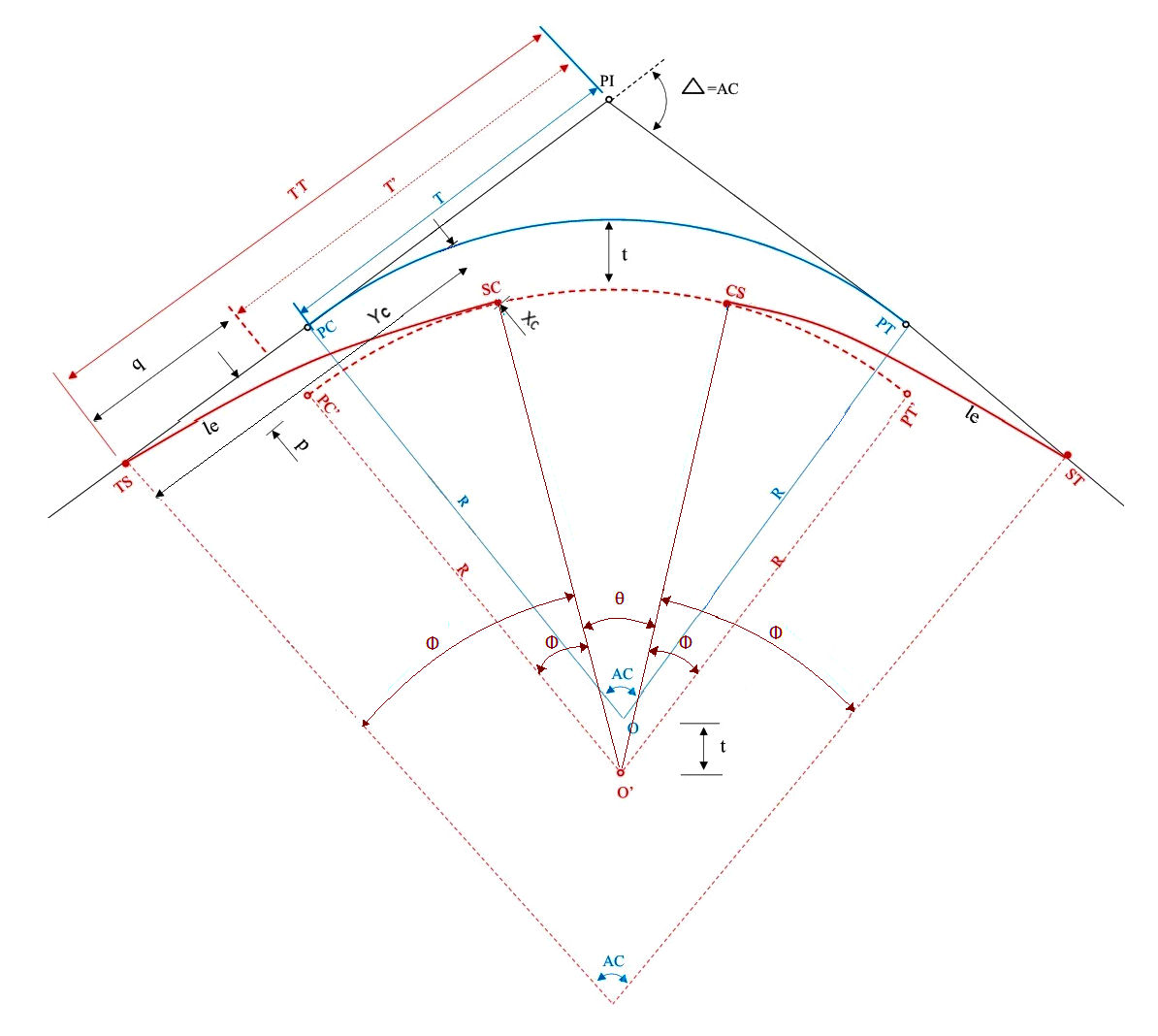
Onde:
- TT é a tangente externa da curva com transição;
- TS e ST são os pontos de início e fim da curva com transição;
- le é o comprimento do trecho em espiral;
- SC é CS são os pontos de início e fim do trecho de curva circular;
- Xc e Yc são as coordenadas de SC;
- PC’ e PT’ são os pontos de início e fim da curva circular, deslocados;
- q e p são as coordenadas de PC’;
- t é o deslocamento da curva circular;
- PI é o ponto de interseção das tangentes;
- Δ é o ângulo de deflexão das tangentes externas;
- AC é o ângulo central da curva de transição;
- θ é ângulo central do trecho circular;
- Φ é o ângulo central do trecho em espiral;
- R é o raio da curva circular;
- O’ é o novo centro da curva circular deslocada.
Agora que já fomos apresentados aos elementos da curva com transição em espiral de raio conservado, iremos agora estudá-los individualmente, a seguir.
Pontos notáveis TS e ST
O ponto TS (tangent-spiral) equivale ao ponto de início da curva de concordância composta por trechos em espiral e um trecho circular, enquanto o ponto ST (spiral-tangent) equivale ao ponto de término da curva de concordância e início do trecho reto.
Esses pontos são, então, calculados por:
\mathrm{TS=PI-TT}
\mathrm{ST=CS+le}
Onde:
- TS é a estaca de início da curva de concordância com transição;
- ST é a estaca de fim da curva de concordância com transição;
- PI é o ponto de interseção das tangentes;
- TT é a tangente externa da curva com transição (m);
- CS é estaca de fim do trecho circular;
- le é o comprimento do trecho em espiral (m).
Pontos notáveis SC e CS
O ponto SC (spital-circular) equivale ao ponto de início do trecho circular, no interior da curva de concordância, enquanto o ponto CS (circular-spiral) equivale ao ponto de término desse mesmo trecho e início do segundo trecho espiral da curva composta.
Esses pontos são, então, calculados por:
\mathrm{SC=TS+le}
\mathrm{CS=SC+D_{θ}}
Onde:
- SC é estaca de início do trecho circular;
- CS é estaca de fim do trecho circular;
- TS é a estaca de início da curva de concordância com transição;
- le é o comprimento do trecho em espiral (m);
- Dθ é o desenvolvimento do trecho circular (m).
Há também outro método para a locação do ponto SC, que se dá através do cálculo de suas coordenadas Xc e Yc, a seguir.
Coordenadas do ponto SC em relação a TS
\mathrm{Xc=\dfrac{le.Φ}{3}\cdot\left(1-\dfrac{Φ^2}{14}+\dfrac{Φ^4}{440}\right)}
\mathrm{Yc=le\left(1-\dfrac{Φ^2}{10}+\dfrac{Φ^4}{216}\right)}
Onde:
- Xc é a abscissa do ponto SC (m);
- Yc é a ordenada do ponto SC (m);
- Φ é o ângulo central do trecho em espiral (rad);
- le é o comprimento do trecho em espiral (m).
Tangente externa da curva com transição
Tangente externa (TT), neste caso, representa os segmentos de reta que vão do TS ao PI ou do PI ao ST. TT é, então, calculado por:
\mathrm{TT=q+[(R+p)\cdot{tg(AC/2)]}}
Onde:
- TT é a tangente externa da curva com transição;
- p é a abscissa do ponto PC’ (m);
- q é a ordenada do ponto PC’ (m);
- R é o raio da curva circular (m);
- AC é o ângulo central da curva de transição (graus).
Coordenadas do ponto PC’ em relação a TS
É importante conhecermos as coordenadas do ponto PC’ para o cálculo de TT e são determinadas por:
\mathrm{p=Xc-R.[1-cos(Φ)]}
\mathrm{q=Yc-R.sen(Φ)}
Onde:
- p é a abscissa do ponto PC’ (m);
- q é a ordenada do ponto PC’ (m);
- Φ é o ângulo central do trecho em espiral (graus);
- R é o raio da curva circular (m).
Comprimento do trecho em espiral
O comprimento do trecho em espiral deve seguir alguns critérios e será determinado de acordo com a média dos comprimentos máximo e mínimo, encontrados a seguir.
Critério de segurança
Esse primeiro critério estabelece o menor valor permitido para o comprimento da transição e usa como parâmetro a distância percorrida por um veículo que trafega na velocidade diretriz, no tempo de 2 s, que é o tempo mínimo de necessário para o giro do volante.
O comprimento é, então, calculado conforme abaixo, lembrando que esse valor não pode ser inferior a 30 m.
\mathrm{le_{mín}=\dfrac{V}{1,8}}
Onde:
- lemín é o comprimento mínimo do trecho em espiral (m), le≥30 m;
- V é a velocidade diretriz da pista (km/h).
Critério dinâmico de Barnett
O segundo critério estabelece uma taxa máxima de variação da aceleração centrífuga, com o objetivo de minimizar os efeitos negativos do surgimento brusco dessa força.
Dessa forma, o comprimento da transição deve ser tal que permita o surgimento gradual do efeito da força centrífuga, conforme abaixo.
\mathrm{le_{mín}=0,036\dfrac{V^3}{R}}
Onde:
- lemín é o comprimento mínimo do trecho em espiral (m), le≥30 m;
- V é a velocidade diretriz da pista (km/h);
- R é o raio da curva circular (m).
Comprimento máximo
O comprimento máximo da transição será o correspondente ao ângulo central nulo da curva circular, ou seja, as espirais se encontram e o desenvolvimento da curva circular é zero.
\mathrm{le_{máx}=R.AC}
Onde:
- lemáx é o comprimento máximo do trecho em espiral (m);
- R é o raio da curva circular (m);
- AC é o ângulo central da curva de transição (rad).
Comprimento a ser adotado
A comprimento que deverá ser adotado para o comprimento do ramo da espiral será a média entre o máximo e mínimo encontrados pelos critérios anteriores, lembrando que o valor resultante deverá ser arredondado para um valor igual a um número inteiro de estacas, ou múltiplo de 10.
\mathrm{le_{adot}=\dfrac{le_{mín}+le_{máx}}{2}}
Onde:
- leadot é o comprimento a ser adotado para o trecho em espiral (m);
- lemín é o comprimento mínimo dentre os critérios (m), lemín ≥ 30 m ;
- lemáx é o comprimento máximo (m).
Ângulo central do trecho em espiral
Os dois ângulo da espiral (Φ) são aqueles que, somados com o ângulo central do trecho circular, resulta no ângulo de deflexão das tangentes externas e são obtidos por:
\mathrm{Φ=\dfrac{le}{2.R}}
Onde:
- Φ é o ângulo central do trecho em espiral (graus);
- le é o comprimento do trecho em espiral (m);
- R é o raio da curva circular (m).
Ângulo central do trecho circular
O ângulo circular (θ) nada mais é do que o ângulo formado entre os pontos SC e CS da curva e é obtido por:
\mathrm{θ=AC-2.Φ}
Onde:
- θ é ângulo central do trecho circular (graus);
- Φ é o ângulo central do trecho em espiral (graus);
- AC é o ângulo central da curva de transição (graus), AC≥2.Φ.
Desenvolvimento do trecho circular
Desenvolvimento da curva (Dθ), neste caso, representa o comprimento do arco que vai desde o SC a CS e é obtido pela seguinte expressão:
\mathrm{D_θ=R.θ}
Onde:
- Dθ é o desenvolvimento do trecho circular (m);
- R é o raio da curva circular (m);
- θ é ângulo central do trecho circular (rad).
Deslocamento da curva circular
Deslocamento (t) é o valor do deslocamento do centro da curva circular para a realização da transição espiral entre a curva circular e a o trecho reto da estrada.
\mathrm{t=\dfrac{p}{cos(AC/2)}}
Onde:
- t é o deslocamento da curva circular (m);
- p é a abscissa do ponto PC’ (m);
- AC é o ângulo central da curva de transição (graus).
Locação da curva horizontal com transição
Agora que já conhecemos todos os elementos da curva com transição, já podemos aprender os procedimentos básicos para a locação desse tipo de curva em uma estrada.
Para isso, observe os procedimentos que serão apresentados no exemplo prático clicando aqui, lembrando que a locação deverá obedecer ao seguinte critério:
- le ≤ 60 m, locar estacas a cada 5 metros;
- Ɩe > 60 m, locar estacas a cada 10 metros.
Pois bem pessoal, essas foram algumas considerações a respeito das curvas horizontais com transição, espero muito que esse post tenha sido útil pra você e se quiser exercitar tudo que aprendeu, clique aqui.
Se gostou, siga a gente aqui, no Youtube e também no Instagram!
Ah, e deixe comentários se tiver alguma dúvida.
Fonte:
ALBUQUERQUE, Marcos. Curva Horizontal com Transição. Teresina: UFPI, 2017.
MACEDO, Edivaldo Lins. Noções de Topografia Para Projetos Rodoviarios. 2008. Disponível em: <http://www.topografiageral.com/>. Acesso em: 26 agosto 2019.

Engenheira Civil pela Universidade Federal do Piauí, engenheira de obra, perita judicial e pós-graduanda em Avaliação, Auditoria e Perícias de Engenharia.


Supondo que seja necessário diminuir a Tangente externa da curva de transição, ou esta já possui um valor definido, qual a sequência de processos que devo adotar no cálculo?
Pedro, muito boa a sua pergunta. Bom, se for possível alterar o traçado da estrada, sugiro começar por diminuir o ângulo de deflexão das tangentes externas (Δ), consequentemente, as demais variáveis da curva, inclusive a tangente externa, serão modificadas. Se isso não for possível, você pode deslocar o centro da curva para a extremidade, lembrando que isso vai diminuir o comprimento da espiral e comprometer o poder de transição da curva. Optanto pela segunda opção, o ponto TS se deslocará à medida que TT diminuir, o ângulo Φ será a metade da diferença entre diferença entre os ângulos Δ e θ e o comprimento da espiral será calculado em função do ângulo Φ (e não com base nos critérios normais). Os demais passos podem ser executados normalmente.
Espero ter ajudado!
COMO QUE CALCULA A VELOCIDADE DA CURVA COM ESPIRAL? POR EXEMPLO RAIO DE 35,00 M E ESPIRAL DE 35,00 M?
Primeiro, precisamos nos atentar que nem o raio e nem a aceleração centrípeta são constantes. Na prática, o que fazemos é considerar a velocidade como sendo constante em todo o trecho na estrada, neste caso, a velocidade diretriz, que depende das características técnicas do projeto.