No nosso post anterior sobre Perda de Carga, explicamos quais os seus tipos, suas características e principais diferenças entre eles. Se não leu ainda, recomendamos que dê uma olhada.
Agora, vamos solidificar o que foi aprendido sobre perda de carga até o momento. Para tanto, propomos alguns exemplos resolvidos tanto sobre perda de carga distribuída como localizada.
Confira abaixo!
Exemplo do cálculo de perda de carga distribuída
Água escoa em um tubo liso com número de Reynolds igual a 106. Depois de vários anos de uso, observa-se que a metade da vazão original produz a mesma perda de carga original. Estime o valor da rugosidade relativa (ԑ/D) do duto deteriorado.
RESOLUÇÃO:
Passo 01: Determinar o fator de atrito inicial (f1)
Para determinar o valor de f será necessário um processo interativo, uma vez que a incógnita aparece dos dois lados da equação.
Dessa forma, começaremos arbitrando um valor qualquer para f” de 1.
\mathrm{\dfrac{1}{\sqrt{f'}}=-2log\left(\dfrac{(ε/D)}{3,7}+\dfrac{2,51}{Re\sqrt{f''}}\right)}
\mathrm{\dfrac{1}{\sqrt{f'}}=-2log\left(0+\dfrac{2,51}{{10}^6\sqrt{1}}\right)}
\mathrm{f'=7,971.10^{-3}}
Agora, faremos novamente os cálculos substituindo o valor de 7,971.10-3 em f” e assim por diante, até os valores de f’ e f” se igualarem.
\mathrm{\dfrac{1}{\sqrt{f'}} =-2log\left(0+\dfrac{2,51}{{10}^6\sqrt{7,971.{10}^{-3}}}\right)}
f’=0,0121
\mathrm{\dfrac{1}{\sqrt {f'}}\ =-2log\left(0+\dfrac{2,51}{{10}^6\sqrt{0,0121}}\right)}
f’=0,0116
\mathrm{\dfrac{1}{\sqrt {f'}}=-2log\left(0+\dfrac{2,51}{{10}^6\sqrt{0,0116}}\right)}
f’=0,0116
Como f’=f’’, o valor de f1 foi encontrado e é igual a 0,0116.
Passo 02: Determinar o fator de atrito final (f2)
Como Q2=Q1/2, então:
v2.A = (v1.A)/2
v2=v1/2
De posse dessa informação e sabendo que Δh1 =Δh2, temos:
\mathrm{\Delta h\ =\ f\ \dfrac{L}{D}\ \dfrac{v^2}{2g}}
\mathrm{f_1\dfrac{L}{D}\ \dfrac{{v_1}^2}{2g}=\ f_2\ \dfrac{L}{D}\ \dfrac{{v_2}^2}{2g}}
\mathrm{f_1\dfrac{L}{D}\ \dfrac{{v_1}^2}{2g}=\ f_2\ \dfrac{L}{D}\ \dfrac{({v_1/2)}^2}{2g}}
\mathrm{ f_1\ =\ f_2/4 f_2=4.0,0116=0,046}
Passo 03: Determinar o novo número de Reynolds (Re2)
\mathrm{Re=\dfrac{ρ.ν.D}{μ}}
Como ρ,D e μ são valores constantes, o novo número de Reynolds varia apenas com a velocidade, logo:
\mathrm{Re_2=Re_1/2=0,5.10^6}
Passo 04: Encontrar o valor de ԑ/D final
\mathrm{\dfrac{1}{\sqrt{f}}=-2log\left(\dfrac{ε/D}{3,71}+\dfrac{2,51}{Re\sqrt{f}}\right)}
\mathrm{\dfrac{1}{\sqrt{0,046}}=-2log\left(\dfrac{ε/D}{3,71}+\dfrac{2,51}{10^6\sqrt{0,046}}\right)}
\mathrm{4,662=-2log\left[0,269\dfrac{ε}{D}+2,340.10^{-5}\right]}
\mathrm{-2,331=log[0,269\dfrac{ε}{D}+2,340.10^{-5}]}
\mathrm{4,664.10^{-3}=0,073\dfrac{ε}{D}+1,122.10^{-5}}
\mathrm{\mathbf{ε/D = 0,0173}}
Exemplo do cálculo de perda de carga localizada
A determinação experimental dos coeficientes e das perdas de carga localizada é feita mediante medidas de pressão e declividades das linhas piezométricas, em trechos de escoamento estabelecido e de vazão. Calcule a perda de carga e o coeficiente de perda de carga para o alargamento gradual mostrado na figura abaixo, em relação à velocidade no tubo de 75mm de diâmetro, a partir dos dados da figura.

RESOLUÇÃO:
Passo 01: Calcular a velocidade do tubo de 75mm (V75)
Sabendo que Q=A.V e que Q75=Q150, temos:
\mathrm{A_{75}.V_{75}=A_{150}.V_{150}}
\mathrm{\left(\pi\dfrac{{0,075}^2}{4}\right)V_{75}=\left(\pi\dfrac{{0,150}^2}{4}\right)3}
\mathrm{V_{75}=12m/s}
Passo 02: Encontrar o valor da carga piezométrica na entrada e na saída do alargamento
Como a linha piezométrica é uma reta é fácil calcular o valor da carga piezométrica tanto para a entrada quanto para a saída do alargamento apenas prologando as retas:
\mathrm{E_{entrada}=\left(\dfrac{1,19-4,12}{1,5}\right).1,8+4,12}
\mathrm{E_{entrada}=0,60m}
\mathrm{E_{saída}=\left(\dfrac{6,9-6,713}{3}\right).6+6,71}
\mathrm{E_{saída}=7,09m}
Passo 03: Calcular a perda d carga (ΔH)
Usando a equação de Bernoulli, E=z+p/γ+v²/2g e E1=E2+ΔH, conforme ilustração abaixo.
Dessa forma, sabendo que a carga piezométrica equivale a z+p/γ, temos:
\mathrm{Z_1+\dfrac{p_1}{γ}+\dfrac{v_1^2}{2g}= z_2+\dfrac{p_2}{γ}+\dfrac{v_2^2}{2g}+ΔH}
\mathrm{0,60+\dfrac{{12}^2}{2.9,81}=7,09+\dfrac{3^2}{2.9,81}+ΔH}
\mathrm{\mathbf{ΔH=0,391m}}
Passo 04: Calcular o coeficiente de perda d carga localizada (K)
\mathrm{ΔH=K\dfrac{v^2}{2g}}
\mathrm{0,391=K\dfrac{{12}^2}{2.9,81}}
\mathrm{\mathbf{K=0,053}}
Exemplo do cálculo de perda de carga total
Se você preferir, a próxima questão também está disponível em vídeo, no nosso canal do YouTube. Confira abaixo!
A instalação hidráulica predial da figura está em um plano vertical e é toda em aço galvanizado novo com diâmetro de 1”, e alimentada por uma vazão de 2l/s de água. Os cotovelos são de raio curto e os registros de gaveta. Determine qual deve ser o comprimento x para que as vazões que saem pelas extremidades A e B sejam iguais.
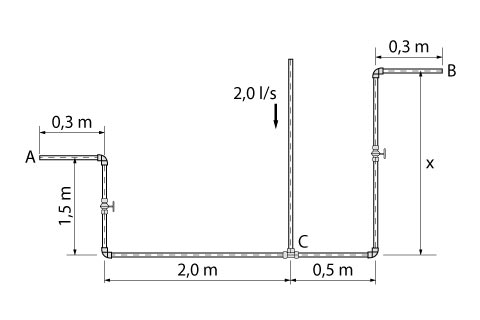
RESOLUÇÃO:
Passo 01: Calcular as velocidades
Como o diâmetro é constante e as vazões de saída são iguais, as velocidades de saída também são iguais.
\mathrm{Q_{entrada}=v_{entrada}.A}
\mathrm{[2.{10}^{-3}] = v_{entrada}.[π.(1.0,025)^2/4]}
\mathrm{v_{entrada}=4,07m/s}
\mathrm{Q_{saída}=v_{saída}.A}
\mathrm{[2.{10}^{-3}/2] = v_{saída}.[π.(1.0,025)^2/4}
\mathrm{v_A=v_B=v_{saída}=2,04m/s}
Passo 03: Calcular a perda de carga distribuída
O valor da perda de carga localizada nos dois trechos, por possuírem os mesmos acessórios, são iguais.
\mathrm{Δh_{dist}=\dfrac{10,643.Q^{1,85}}{C^{1,85}.D^{4,87}}L}
\mathrm{Δh_{CA,dist}=\dfrac{10,643.{(1.{10}^{-3})}^{1,85}}{{125}^{1,85}.(1.0,025)^{4,87}}(3,8)}
\mathrm{Δh_{CA,dist}=0,954m}
\mathrm{Δh_{CB,dist}=\dfrac{10,643.{(1.{10}^{-3})}^{1,85}}{{125}^{1,85}.(1.0,025)^{4,87}}(0,8+x)}
\mathrm{Δh_{CA,dist}=0,251.(0,8+x)}
Passo 04: Calcular a perda de carga localizada
O valor da perda de carga localizada nos dois trechos, por possuírem os mesmos acessórios, são iguais.
\mathrm{Δh_{CA,loc}=Δh_{CB,loc}=Δh_{loc}}
Passo 05: Calcular a perda de carga total
\mathrm{Δh_{total}=Δh_{dist}+Δh_{loc}}
\mathrm{Δh_{CA,total}=0,954+Δh_{loc}}
\mathrm{Δh_{CB,total}=0,251(0,8+x)+Δh_{loc}}
Passo 06: Encontrar o valor de x
Pelo princípio de Bernoulli \mathrm{E_C=E_A+Δh_{CA,total}} e \mathrm{E_C=E_B+ Δh_{CB,total}}, logo:
\mathrm{E_A+Δh_{CA,total}=E_B+ Δh_{CB,total}}
\mathrm{Z_A+\dfrac{p_A}{γ}+\dfrac{{v_A}^2}{2g}=Z_B+\dfrac{p_B}{γ}+\dfrac{{v_B}^2}{2g}+ ...}
\mathrm{\cdots+(Δh_{CB,total}-Δh_{CA,total})}
Como as velocidades e as pressões nos extremos da tubulação são iguais, temos:
\mathrm{1,5=x+[0,251(0,8+x)+Δh_{loc}+...}
\mathrm{\cdots-(0,954+Δh_{loc})]}
\mathrm{1,251x=2,253}
\mathrm{\mathbf{x=1,80m}}
Espero que tenhamos lhe ajudado. Se gostou, não deixe de seguir nosso blog para receber mais posts como este!
E se ainda ficou com alguma dúvida, deixe nos comentários abaixo.

Engenheira Civil pela Universidade Federal do Piauí, engenheira de obra, perita judicial e pós-graduanda em Avaliação, Auditoria e Perícias de Engenharia.


Boa tarde!
O diâmetro da área em metro não seria 0,075m?
Pq vc uso 0,75?
Obrigada pela observação, Junior, foi apenas um erro.
Oi Dandara, bom dia
Na questão de perda de carga localizada você faz um cálculo de Energia de entrada e saída, contudo você usa a linha piezométrica, no caso o que você calcula é a Cota piezométrica, já que lá na frente você soma os resultados com a carga cinética.
Faz sentido a minha observação?
Oi Bárbara, faz sentido sim!